Алгебраическая кривая

Кубика Чирнгауза — алгебраическая кривая третьего порядка.

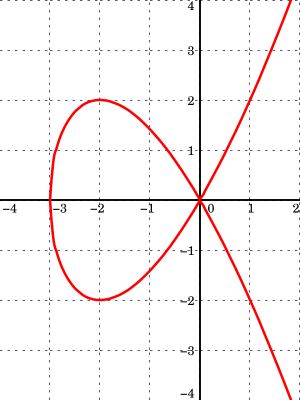
Алгебраическая кривая, или плоская алгебраическая кривая, — это, в простейшем случае, множество нулей многочлена двух переменных. Степенью, или порядком, алгебраической кривой называется степень этого многочлена.

Например, единичная окружность, задающаяся уравнением $x^{2}+y^{2}=1$, является алгебраической кривой второй степени, поскольку совпадает с множеством нулей многочлена $x^{2}+y^{2}-1$.

Плоские алгебраические кривые с первой по восьмую степень соответственно называют прямыми, кониками, кубиками, квартиками, пентиками, секстиками, септиками и октиками. В алгебраической геометрии также рассматривают не только вещественные нули многочленов, но и комплексные. Более того, многочлены могут рассматриваться над произвольными полями.

Так, обобщенная плоская аффинная алгебраическая кривая над полем $k$ определяется как множество тех пар из $K\times K$, где $K$ — алгебраическое замыкание поля $k$, которые являются корнями многочлена от двух переменных с коэффициентами в $k$. Такие пары называются точками этой кривой. Те точки кривой, каждая координата которых лежит в $k$, называются $k$-точками, а множество $k$-точек называется $k$-частью кривой.

Например, точка $(2,{\sqrt {-3}})$ принадлежит рассмотренной выше единичной окружности, однако не принадлежит её вещественной $\mathbb {R}$-части. Кроме того, многочлен $x^{2}+y^{2}+1$ задаёт алгебраическую кривую, вещественная часть которой пуста. Тем не менее, сама кривая не является пустой.

Также в алгебраической геометрии рассматривают более общие алгебраические кривые, которые содержатся не обязательно в двумерных, а в пространствах с большим числом измерений, и также в проективных пространствах.

Оказывается, многие свойства алгебраической кривой не зависят от выбора конкретного вложения в некоторое пространство, что приводит к следующему общему определению алгебраической кривой.

Алгебраическая кривая — это алгебраическое многообразие размерности 1. Иными словами, алгебраическая кривая — это алгебраическое многообразие, каждое алгебраическое подмногообразие которого является одноточечным.

Примеры алгебраических кривых

Рациональные кривые

Рациональная кривая, также известная как уникурсальная кривая, — это кривая, бирационально эквивалентная аффинной прямой (или проективной прямой); другими словами, кривая, допускающая рациональную параметризацию.

Более конкретно, рациональная кривая в n-мерном пространстве может быть параметризована (за исключением некоторого числа изолированных «особых точек») при помощи n рациональных функций от единственного параметра t.

Любое коническое сечение над полем рациональных чисел, содержащее хотя бы одну рациональную точку, является рациональной кривой. Её можно параметризовать, проведя через рациональную точку прямую с произвольным угловым коэффициентом t и сопоставив данному t вторую точку пересечения прямой и коники (их не может быть больше двух).

Эллипс. x² + xy + y² = 1

Например, рассмотрим эллипс x² + xy + y² = 1 с рациональной точкой (−1, 0). Проведя через неё прямую y = t(x + 1), подставив выражение y через x в уравнение и решив относительно x, получим уравнения

$x={\frac {1-t^{2}}{1+t+t^{2}}},$

$y=t(x+1)={\frac {t(t+2)}{1+t+t^{2}}}\,,$

задающие рациональную параметризацию эллипса. В таком виде представимы все точки эллипса, кроме точки (−1, 0); можно сопоставить ей t = ∞, то есть параметризовать эллипс проективной прямой.

Эту рациональную параметризацию можно рассматривать как параметризацию «эллипса в проективном пространстве», перейдя к однородным координатам, то есть заменив t на T/U, а x, y — на X/Z, Y/Z соответственно. Параметризация эллипса X² + XY + Y² = Z² проективной прямой примет следующий вид:

$X=U^{2}-T^{2},\quad Y=T\,(T+2\,U),\quad Z=T^{2}+TU+U^{2}.$

Эллиптические кривые

Рациональные кривые (над алгебраически замкнутым полем) — это в точности алгебраические кривые рода 0 (см. ниже), в этой терминологии эллиптические кривые — это кривые рода 1 с рациональной точкой. Любая такая кривая может быть представлена как кубика без особенностей.

Эллиптическая кривая несёт на себе структуру абелевой группы. Сумма трёх точек на кубике равна нулю тогда и только тогда, когда эти точки коллинеарны.

Пересечение двух коник является кривой четвёртого порядка рода 1, а значит, эллиптической кривой, если содержит хотя бы одну рациональную точку. В противном случае пересечение может быть рациональной кривой четвёртого порядка с особенностями, или быть разложимым на кривые меньшего порядка (кубика и прямая, две коники, коника и две прямые или четыре прямые).

Связь с полями функций

Изучение алгебраических кривых может быть сведено к изучению неприводимых кривых (то есть не раскладывающихся в объединение двух меньших кривых). Каждой такой кривой можно сопоставить поле рациональных функций на ней; оказывается, что кривые бирационально эквивалентны тогда и только тогда, когда их поля функций изоморфны. Это значит, что категория алгебраических кривых и рациональных отображений двойственна категории одномерных полей алгебраических функций, то есть полей, являющихся алгебраическими расширениями поля $k(x)$.

Комплексные кривые как действительные поверхности

Комплексная алгебраическая кривая, вложенная в аффинное или проективное пространство, имеет топологическую размерность 2, другими словами, является поверхностью. В частности, комплексная алгебраическая кривая без особенностей является двумерным ориентируемым многообразием.

Топологический род этой поверхности совпадает с родом алгебраической кривой (который можно вычислить алгебраическими способами). Если проекция кривой без особенностей на плоскость является алгебраической кривой степени d с простейшими особенностями (обыкновенными двойными точками), то исходная кривая имеет род (d − 1)(d − 2)/2 − k, где k — число этих особенностей.

Изучение компактных римановых поверхностей состоит фактически в изучении комплексных алгебраических кривых без особенностей, рассматриваемых как поверхности с дополнительной аналитической структурой. Более точно, следующие категории эквивалентны:

• Категория проективных алгебраических кривых без особенностей (с рациональными отображениями в качестве морфизмов).
• Категория компактных римановых поверхностей и голоморфных функций.

Классификация особенностей

x³ − y² = 0

Особые точки включают в себя несколько типов точек, в которых кривая «пересекает сама себя», а также различные типы точек возврата. Например, на рисунке показана кривая x³ − y² = 0 с точкой возврата в начале координат.

Особые точки можно классифицировать по их инвариантам. Например, особую точку с дельта-инвариантом δ можно интуитивно описать как точку, в которой встречаются сразу δ «самопересечений». В случае точки P на неприводимой кривой δ можно вычислить как длину модуля ${\widetilde {{\mathcal {O}}_{P}}}/{\mathcal {O}}_{P}$, где ${\mathcal {O}}_{P}$ — локальное кольцо в точке P и ${\widetilde {{\mathcal {O}}_{P}}}$ — его целое замыкание. Вычисление дельта-инвариантов всех особых точек позволяет вычислить род кривой по формуле:

$g={\frac {1}{2}}(d-1)(d-2)-\sum _{P}\delta _{P},$

Другие важные инварианты: кратность m особенности (максимальное целое число, такое что все производные задающего кривую многочлена, порядок которых не превосходит m, равны нулю) и число Милнора.

См. также

• Категория Алгебраические кривые

Литература

• Ж.-П. Серр. Алгебраические группы и поля классов. — М.: Мир, 1968. — 285 с.
• Джон Милнор. Особые точки комплексных гиперповерхностей. — М.: Мир, 1971. — 121 с.
• Egbert Brieskorn, Horst Knörrer. Plane Algebraic Curves. — Birkhäuser, 1986.
• Hershel M. Farkas, Irwin Kra. Riemann Surfaces. — Springer, 1980.
• W. Fulton. Algebraic Curves: an introduction to algebraic geometry.
• C.G. Gibson. Elementary Geometry of Algebraic Curves: An Undergraduate Introduction. — Cambridge University Press, 1998.
• специальные плоские кривые [1] Архивная копия от 21 июня 2018 на Wayback Machine (рус.)