Алгоритм Грэхема

Алгоритм Грэхема — алгоритм построения выпуклой оболочки в двухмерном пространстве. В этом алгоритме задача о выпуклой оболочке решается с помощью стека, сформированного из точек-кандидатов. Все точки входного множества заносятся в стек, а потом точки, не являющиеся вершинами выпуклой оболочки, со временем удаляются из него. По завершении работы алгоритма в стеке остаются только вершины оболочки в порядке их обхода против часовой стрелки.

Алгоритм

В качестве входных данных процедуры Graham выступает множество точек Q, где $|Q|\geqslant 3$. В ней вызывается функция Top(S), которая возвращает точку, находящуюся на вершине стека S, не изменяя при этом его содержимое. Кроме того, используется также функция NextToTop(S), которая возвращает точку, расположенную в стеке S, на одну позицию ниже от верхней точки; стек S при этом не изменяется.

Graham(Q)
1) Пусть $p_0$ — точка из множества Q с минимальной координатой y или самая левая из таких точек при наличии совпадений
2) Пусть $<p_1, p_2,\ldots,p_m>$ — остальные точки множества Q, отсортированные в порядке возрастания полярного угла,
      измеряемого против часовой стрелки относительно точки $p_0$ 
     (если полярные углы нескольких точек совпадают, то по расстоянию до точки $p_0$)
3) Push($p_0$,S)
4) Push($p_1$,S)
5) for i = 2 to m do
6)     while угол, образованный точками NextToTop(S),Top(S) и $p_i$, образуют не левый поворот
            (при движении по ломаной, образованной этими точками, мы движемся прямо или вправо)
7)       do Pop(S)
8)    Push($p_i$,S)
9) return S

Для определения, образуют ли три точки $a$, $b$ и $c$ левый поворот, можно использовать обобщение векторного произведения на двумерное пространство, а именно условие левого поворота будет выглядеть следующим образом: $u_x v_y - u_y v_x > 0$, где $u = \left\{ b_x - a_x, \; b_y - a_y \right\}, v = \left\{ c_x - a_x, \; c_y - a_y \right\}$

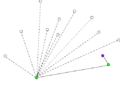
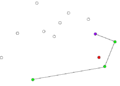
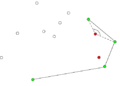
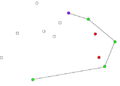
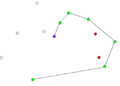
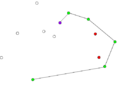
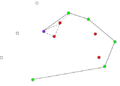
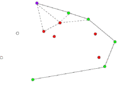
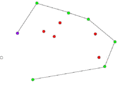
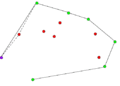
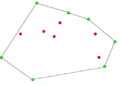
• Пример работы алгоритма Грэхема.
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

Корректность сканирования по Грэхему

Если процедура Graham обрабатывает множество точек Q, где $|Q|\geqslant 3$, то по завершении этой процедуры стек S будет содержать (в направлении снизу вверх) только вершины оболочки CH(Q) в порядке обхода против часовой стрелки.

  

Доказательство  

После выполнения строки 2 в нашем распоряжении имеется последовательность точек $<p_1, p_2,\ldots,p_m>$. Определим подмножество точек $Q_i = \left\{p_0,p_1,\ldots,p_i\right\}$ при i = 2,3,…,m. Множество точек Q — $Q_m$ образуют те из них, что были удалены из-за того, что их полярный угол относительно точки p0 совпадает с полярным углом некоторой точки из множества $Q_m$. Эти точки не принадлежат выпуклой оболочке CH(Q), так что CH($Q_m$) = CH(Q). Таким образом, достаточно показать, что по завершении процедуры Graham стек S состоит из вершин оболочки CH($Q_m$) в порядке обхода против часовой стрелки, если эти точки просматриваются в стеке снизу вверх. Заметим, что точно так же, как точки $p_0$,$p_1$,$p_m$ являются вершинами оболочки CH(Q), точки $p_0$,$p_1$,$p_i$ являются вершинами оболочки CH($Q_i$).

В доказательстве используется сформулированный ниже инвариант цикла. В начале каждой итерации цикла for в строках 6-9 стек S состоит(снизу вверх) только из вершин оболочки CH($Q_{i-1}$) в порядке их обхода против часовой стрелки.

Инициализация. При первом выполнении строки 6 инвариант поддерживается, поскольку в этот момент стек S состоит только из вершин $Q_2$ = $Q_{i-1}$, и это множество трех вершин формирует свою собственную выпуклую оболочку. Кроме того, если просматривать точки снизу вверх, то они будут расположены в порядке обхода против часовой стрелки.

Сохранение. При входе в новую итерацию цикла for вверху стека S находится точка $p_{i-1}$, помещенная туда в конце предыдущей итерации (или перед первой итерацией, когда i = 3). Пусть $p_j$ — верхняя точка стека S после выполнения строк 7-8 цикла while, но перед тем, как в строке 9 в стек будет помещена точка $p_i$. Пусть также $p_k$ — точка, расположенная в стеке S непосредственно под точкой $p_j$. В тот момент, когда точка $p_j$ находится наверху стека S, а точка $p_i$ ещё не добавлена, стек содержит те же точки, что и после j-й итерации цикла for. Поэтому, согласно инварианту цикла, в этот момент стек S содержит только CH($Q_j$) в порядке их обхода против часовой стрелки, если просматривать их снизу вверх. Полярный угол точки $p_i$ относительно точки $p_0$ больше, чем полярный угол точки $p_j$, и поскольку угол $p_k$$p_j$$p_i$ сворачивает влево(в противном случае точка $p_j$ была бы снята со стека), после добавления в стек S точки $p_i$ (до этого там были только вершины CH($Q_j$)) в нем будут содержаться вершины CH($Q_j \cup \left\{p_i\right\}$). При этом они будут расположены в порядке обхода против часовой стрелки, если просматривать их снизу вверх.

Покажем, что множество вершин CH($Q_j \cup \left\{p_i\right\}$) совпадает с множеством точек CH($Q_i$). Рассмотрим произвольную точку $p_t$, снятую со стека во время выполнения i-й итерации цикла for, и пусть $p_r$ — точка, расположенная в стеке S непосредственно под точкой $p_t$ перед снятием со стека последней(этой точкой pr может быть точка $p_j$). Угол $p_r$$p_t$$p_i$ не сворачивает влево, и полярный угол точки $p_t$ относительно точки $p_0$ больше полярного угла точки $p_r$. Так как точка $p_t$ находится внутри треугольника, образованного тремя другими точками множества $Q_i$, она не может быть вершиной CH($Q_i$). Так как $p_t$ не является вершиной CH($Q_i$), то CH($Q_i$ — {$p_t$}) = CH($Q_i$). Пусть $P_i$ — множество точек, снятых сто стека во время выполнения i-ой итерации цикла for. Верно равенство CH($Q_i$ — $P_i$) = CH($Q_i$). Однако $Q_i$ — $P_i$ = $Q_i$ $\cup$ {$p_i$}, поэтому мы приходим к заключению, что CH($Q_j$ $\cup$ {$p_i$}) = CH($Q_i$ — $P_i$) = CH($Q_i$).

Сразу после вытеснения из стека S точки $p_i$ в нем содержатся только вершины CH($Q_i$) в порядке их обхода против часовой стрелки, если просматривать их в стеке снизу вверх. Последующее увеличение на единицу значения i приведет к сохранению инварианта цикла в очередной итерации.

Завершение. По завершении цикла выполняется равенство i = m + 1, поэтому из инварианта цикла следует, что стек S состоит только из вершин CH($Q_m$), то есть из вершин CH(Q). Эти вершины расположены в порядке обхода против часовой стрелки, если они просматриваются в стеке снизу вверх.

Время работы

Время работы процедуры Graham равно O(n lg n), где n = |Q|. Как несложно показать, циклу while потребуется время O(n). В то время, как сортировка полярных углов займет O(n lg n) времени, откуда и следует общая асимптотика процедуры Graham.

См. также

• Алгоритм Джарвиса
• Алгоритм Чана
• Алгоритм быстрой оболочки

Литература

• Т. Кормен, Ч. Лейзерсон, Р.Ривест, К.Штайн Алгоритмы. Построение и анализ. = Introduction to Algorithms. — 2-e изд. — “Вильямс”, 2005.

Ссылки

• Визуализатор
• Реализация на c++
• Реализация на Java