Алгоритм Катхилла — Макки

Упорядочение обратным алгоритмом Катхилла — Макки

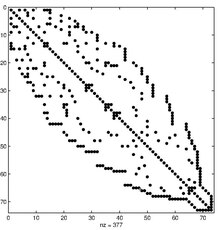
Алгоритм Ка́тхилла — Макки́ (англ. Cuthill–McKee) — алгоритм уменьшения ширины ленты разреженных симметричных матриц. Назван по именам разработчиков — Элизабет Катхилл и Джеймса Макки.

Обратный алгоритм Катхилла — Макки (RCM, reverse Cuthill—McKee) — тот же самый алгоритм с обратной нумераций индексов.

Алгоритм

Исходная симметричная матрица $n\times n$ рассматривается как матрица смежности графа $(V,E)$. Алгоритм Катхилла — Макки перенумеровывает вершины графа таким образом, чтобы в результате соответствующей перестановки столбцов и строк исходной матрицы уменьшить ширину её ленты.

Алгоритм строит упорядоченный набор вершин $R$, представляющий новую нумерацию вершин. Для связного графа алгоритм выглядит следующим образом:

1. выбрать периферийную вершину (или псевдопериферийную вершину) $v$ для начального значения кортежа $R:=(v)$;
2. для $i=1,2,...$, пока выполнено условие $|R|<n$, выполнять шаги 3-5:
3. построить множество смежности $\operatorname {Adj} (R_{i})$ для $R_{i}$, где $R_{i}$ — $i$-ая компонента $R$, и исключить вершины, которые уже содержатся в $R$, то есть: $A_{i}:=\operatorname {Adj} (R_{i})\setminus R$;
4. отсортировать $A_{i}$ по возрастанию степеней вершин;
5. добавить $A_{i}$ в кортеж результата $R$.

Другими словами, алгоритм нумерует вершины в ходе поиска в ширину, при котором смежные вершины обходятся в порядке увеличения их степеней.

Для несвязного графа алгоритм можно применить отдельно к каждой компоненте связности.

Временна́я вычислительная сложность алгоритма RCM при условии, что для упорядочения применена сортировка вставками, $O(m|E|)$, где $m$ — максимальная степень вершины, $|E|$ — количество ребер графа.

Выбор начальной вершины

Для получения хороших результатов необходимо найти периферийную вершину графа $(V,E)$. Эта задача в общем случае является достаточно трудной, поэтому вместо неё обычно ищут псевдопериферийную вершину с помощью одной из модификаций эвристического алгоритма Гиббса и др.

Для описания алгоритма вводится понятие корневой структуры уровней (англ. rooted level structure). Для заданной вершины $v$ структурой уровней с корнем в $v$ будет разбиение ${\mathcal {L}}$ множества вершин $V$:

${\mathcal {L}}(v)=\{L_{0}(v),L_{1}(v),\dots ,L_{l(v)}(v)\},$

где подмножества $L_{i}(v)$ определены следующий образом:

$L_{0}(v)=\{v\},$

$L_{1}(v)=\operatorname {Adj} (L_{0}(v))$

и

$L_{i}(v)=\operatorname {Adj} (L_{i-1}(v))-L_{i-2}(v),\qquad i=2,3,\dots ,l(v).$

Алгоритм нахождения псевдопериферийной вершины:

1. выбрать произвольную вершину $r$ из $V$;
2. построить структуру уровней для корня $r$: ${\mathcal {L}}(r)=\{L_{0}(r),L_{1}(r),\dots ,L_{l(r)}(r)\}$;
3. выбрать вершину с минимальной степенью $v$ из $L_{l(r)}(r)$;
4. построить структуру уровней для корня $v$: ${\mathcal {L}}(v)=\{L_{0}(v),L_{1}(v),\dots ,L_{l(v)}(v)\}$;
5. если $l(v)>l(r)$, то присвоить $r:=v$ и перейти к шагу 3;
6. вершина $v$ является искомой псевдопериферийной вершиной.

Литература

• E. Cuthill and J. McKee. Reducing the bandwidth of sparse symmetric matrices In Proc. 24th Nat. Conf. ACM, pages 157—172, 1969.
• Джордж А., Лю Дж. Численное решение больших разреженных систем уравнений = Computer Solution of Large Sparse Positive Definite Systems. — М.: Мир, 1984. — 333 с.

Ссылки

• Документация по алгоритму Катхилла-Макки для библиотек Boost C++.
• Подробное объяснение алгоритма Катхилла-Макки.
• Подробное объяснение алгоритма Катхилла-Макки (рус.) (недоступная ссылка).
• Реализация алгоритма Катхилла-Макки на Python (недоступная ссылка).