Диаграмма Хассе

Диаграмма Хáссе — вид диаграмм, используемый для представления конечного частично упорядоченного множества в виде рисунка его транзитивного сокращения. Конкретно, для частично упорядоченного множества $(S,\leq )$ диаграмма представляет каждый элемент $S$ как вершины на плоскости и отрезки или кривые, идущие вверх от элемента $x$ к элементу $y$, если $x\leq y$ и не существует элемента $z$, для которого $x<z<y$. Эти кривые могут пересекаться, но не должны проходить через вершины, если только они не являются концами линии. Такая диаграмма с помеченными вершинами однозначно определяют частичный порядок.

Впервые систематически такого рода визуализация описана Биркгофом в 1948 году, им же дано название в честь использовавшего подобные диаграммы Хельмута Хассе, однако такого рода рисунки встречаются и в более ранних трудах, например, в учебнике французского математика Анри Фохта (нем. Henri Vogt) 1895 года издания.

Удобство диаграмм

Хотя диаграммы Хассе является простым и интуитивно ясным средством для работы с конечным частично упорядоченным множеством, весьма сложно нарисовать «хорошую», удобную для визуального восприятия диаграмму для достаточно нетривиального множества из-за большого количества возможных вариантов отображения. Простая техника, предполагающая начать с минимальных элементов и рисовать вышележащие элементы последовательно часто дает плохие результаты — симметрии и внутренние структуры легко потерять.

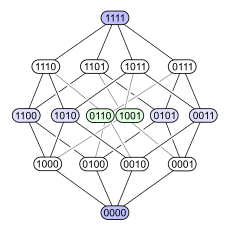
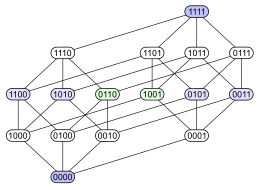
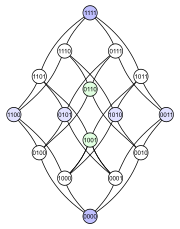
Например, булеан множества из четырёх элементов, упорядоченного операцией включения $\subseteq$, может быть представлен любой из четырёх нижеприведённых диаграмм (каждое подмножество снабжено меткой с бинарной кодировкой, показывающей, содержится соответствующий элемент в подмножестве — 1, или нет — 0):

Первая диаграмма демонстрирует структуру уровней. Вторая диаграмма имеет ту же структуру уровней, но на ней некоторые рёбра удлинены, чтобы подчеркнуть, что четырёхмерный куб является объединением двух трёхмерных. Третья диаграмма показывает некоторую внутреннюю симметрию. В четвёртой диаграмме вершины упорядочены подобно матрице 4×4.

Планарность

Диаграмма Хассе подгрупповой решётки диэдрической группы $\mathrm {Dih} _{4}$ не имеет пересекающихся рёбер.

Некоторые свойства частичных порядков относительно планарности их диаграммы Хассе (то есть возможности нарисовать её без пересечения рёбер):

• Если частичный порядок является решёткой, то его можно нарисовать без пересечений тогда и только тогда, когда размерность порядка не менее двух.
• Если частичный порядок имеет по меньшей мере один минимальный или максимальный элемент, то можно за линейное время проверить, существует ли диаграмма без пересечений.
• Определить, можно ли частичный порядок представить планарной диаграммой Хассе, в общем случае — NP-полная задача.
• Если заданы $y$-координаты элементов частичного порядка, то за линейное время может быть найдена его диаграмма Хассе, сохраняющая заданные координаты, если только такая диаграмма существует. В частности, если частный порядок имеет уровни, можно за линейное время определить, имеется ли диаграмма Хассе без пересечений, у которой высота каждой вершины пропорциональна её рангу.

Литература

• Лекция 3. Частично упорядоченные множества (ЧУМ). Диаграмма Хассе. Максимальные, минимальные, наибольший и наименьший элементы. Цепи и антицепи, длина и ширина конечных ЧУМ. Теорема о разбиении ЧУМ на антицепи. Теорема Дилуорса. Булев куб, его длина и ширина. Булеан.
• K. A. Baker, P. Fishburn, F. S. Roberts. Partial orders of dimension 2 // Networks. — 1971. — Т. 2, № 1. — С. 11–28. — doi:10.1002/net.3230020103..
• G. Birkhoff. Lattice Theory. — 2nd. — American Mathematical Society, 1948.

  Перевод на русский: Г. Биркгоф. Теория структур / Пер. М. И. Граева. — 2-е изд.. — М.: Иностранная литература, 1952. — 408 с.

• A. Garg, R. Tamassia. Upward planarity testing // Order. — 1995. — Т. 12, № 2. — С. 109–133. — doi:10.1007/BF01108622..
• R. Freese. Automated lattice drawing // Concept Lattices. — Springer-Verlag, 2004. — Т. 2961. — С. 589–590..
• M. Jünger, S. Leipert. Level planar embedding in linear time // Proc. of International Symposium on Graph Drawing GD ’99. — 1999. — Т. 1731. — С. 72–81. — ISBN 978-3-540-66904-3. — doi:10.1007/3-540-46648-7_7.
• H. G. Vogt. Leçons sur la résolution algébrique des équations. — Nony, 1895. — С. 91.

Ссылки

• Weisstein, Eric W. Hasse Diagram (англ.) на сайте Wolfram MathWorld.