Коэффициент пропускания
| Коэффициент пропускания | |
|---|---|
| Размерность | безразмерная |
| Примечания | |
| скалярная величина | |
Коэффицие́нт пропуска́ния — безразмерная физическая величина, равная отношению потока излучения , прошедшего через среду, к потоку излучения , упавшему на её поверхность[1]:
В общем случае значение коэффициента пропускания [2] тела зависит как от свойств самого тела, так и от угла падения, спектрального состава и поляризации излучения.
Численно коэффициент пропускания выражают в долях или в процентах.
Коэффициент пропускания неактивных сред всегда меньше 1. В активных средах коэффициент пропускания больше или равен 1, при прохождении излучения через такие среды происходит его усиление. Активные среды используются в качестве рабочих сред лазеров[3][4][5][6].
Коэффициент пропускания связан с оптической плотностью соотношением:
Сумма коэффициента пропускания и коэффициентов отражения, поглощения и рассеяния равна единице. Это утверждение следует из закона сохранения энергии.
Производные, связанные и родственные понятия[править | править код]
Вместе с понятием «коэффициент пропускания» широко используются и другие созданные на его основе понятия. Часть из них представлена ниже.
Коэффициент направленного пропускания [править | править код]
Коэффициент направленного пропускания равен отношению потока излучения, прошедшего сквозь среду, не испытав рассеяния, к потоку падающего излучения.
Коэффициент диффузного пропускания [править | править код]
Коэффициент диффузного пропускания равен отношению потока излучения, прошедшего сквозь среду и рассеянного ею, к потоку падающего излучения.
В отсутствие поглощения и отражений выполняется соотношение:
Спектральный коэффициент пропускания [править | править код]
Коэффициент пропускания монохроматического излучения называют спектральным коэффициентом пропускания. Выражение для него имеет вид:
где и — потоки падающего на среду и прошедшего через неё монохроматического излучения соответственно.
Коэффициент внутреннего пропускания [править | править код]
Коэффициент внутреннего пропускания отражает только те изменения интенсивности излучения, которые происходят внутри среды, то есть потери из-за отражений на входной и выходной поверхностях среды им не учитываются.
Таким образом, по определению:
где — поток излучения, вошедшего в среду, а — поток излучения, дошедшего до выходной поверхности.
С учетом отражения излучения на входной поверхности соотношение между потоком излучения , вошедшего в среду, и потоком излучения , падающим на входную поверхность, имеет вид:
где — коэффициент отражения от входной поверхности.
На выходной поверхности также происходит отражение, поэтому поток излучения , падающего на эту поверхность, и поток , выходящий из среды, связаны соотношением:
где — коэффициент отражения от выходной поверхности. Соответственно, выполняется:
В результате для связи и получается:
Коэффициент внутреннего пропускания обычно используется не при описании свойств тел, как таковых, а как характеристика материалов, преимущественно оптических[7].
Спектральный коэффициент внутреннего пропускания [править | править код]
Спектральный коэффициент внутреннего пропускания представляет собой коэффициент внутреннего пропускания для монохроматического света.
Интегральный коэффициент внутреннего пропускания [править | править код]
Интегральный коэффициент внутреннего пропускания для белого света стандартного источника A (с коррелированной цветовой температурой излучения T=2856 K) рассчитывается по формуле[7][8]:
или следующей из неё:
где — спектральная плотность потока излучения, вошедшего в среду, — спектральная плотность потока излучения, дошедшего до выходной поверхности, а — относительная спектральная световая эффективность монохроматического излучения для дневного зрения[9].
Аналогичным образом определяются интегральные коэффициенты пропускания и для других источников света.
Интегральный коэффициент внутреннего пропускания характеризует способность материала пропускать свет, воспринимаемый человеческим глазом, и является поэтому важной характеристикой оптических материалов[7].
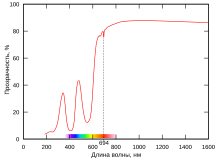
Спектр пропускания[править | править код]
Спектр пропускания — это зависимость коэффициента пропускания от длины волны или частоты (волнового числа, энергии кванта и т. д.) излучения. Применительно к свету такие спектры называют также спектрами светопропускания.
Спектры пропускания являются первичным экспериментальным материалом, получаемым при исследованиях, выполняемых методами абсорбционной спектроскопии. Такие спектры представляют и самостоятельный интерес, например, как одна из основных характеристик оптических материалов[10].
См. также[править | править код]
Примечания[править | править код]
- ↑ Пропускания коэффициент // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 149. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ ГОСТ 8.654-2016 допускает также использование греческой
- ↑ ГОСТ 15093-90 «Лазеры и устройства управления лазерным излучением. Термины и определения».
- ↑ Справочник по лазерам. Пер. с англ. под ред. А. М. Прохорова. Тт. 1—2. — М., 1978.
- ↑ Звелто О. Физика лазеров. Пер. с англ. 2-е изд. — М., 1984.
- ↑ Карлов Н. В. Лекции по квантовой электронике. — М., 1983.
- ↑ 1 2 3 Бесцветное оптическое стекло СССР. Каталог. Под ред. Петровского Г. Т.. — М.: Дом оптики, 1990. — 131 с. — 3000 экз.
- ↑ Зверев В. А., Кривопустова Е. В., Точилина Т. В. Оптические материалы. Часть 1. — Санкт-Петербург: ИТМО, 2009. — С. 95. — 244 с. Архивировано 28 марта 2018 года.
- ↑ ГОСТ 8.332-2013 «Государственная система обеспечения единства измерений. Световые измерения. Значения относительной спектральной световой эффективности монохроматического излучения для дневного зрения. Общие положения»
- ↑ Цветное оптическое стекло и особые стекла. Каталог. Под ред. Петровского Г. Т.. — М.: Дом оптики, 1990. — 229 с. — 1500 экз.
Литература[править | править код]
- ГОСТ 8.654-2016 «Государственная система обеспечения единства измерений. Фотометрия. Термины и определения»
- ГОСТ 7601-78 «Физическая оптика. Термины, буквенные обозначения и определения основных величин»
- ГОСТ Р 8.829-2013 «Государственная система обеспечения единства измерений. Методика измерений оптической плотности (коэффициента пропускания) и мутности пластин и пленок из полимерных материалов»
- Физический энциклопедический словарь. — Советская энциклопедия, 1984. — С. 590.































