Нечётный граф

Граф Петерсена O₃ = KG_5,2
вершин = ${\tbinom {2n-1}{n-1}}$
ребер = $n{\tbinom {2n-1}{n-1}}/2$
диаметр = n − 1
обхват=
  3 если n = 2,
  5 если n = 3,
  6 если n > 3
свойства = дистанционно-транзитивен
обозначение = O_n

Нечётный граф O₄ = KG_7,3

Нечётные графы O_n — семейство симметричных графов с высоким нечётным обхватом, определённых на некоторых семействах множеств. Они включают и обобщают графы Петерсена.

Определения и примеры

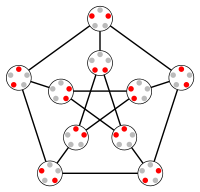
Нечётный граф O_n имеет одну вершину для каждого из (n − 1)-элементных подмножеств множества из (2n − 1) элементов. Две вершины связаны ребром в том и только в том случае, если соответствующие подмножества не пересекаются. Так, O_n — это граф Кнесера KG(2n − 1,n − 1), O₂ — треугольник, а O₃ — знакомый граф Петерсена.

Обобщённые нечётные графы включают нечётные графы и складные кубические графы, и определяются как дистанционно-регулярные графы с диаметром n − 1 и нечётным обхватом 2n − 1 для некоторого n.

История и приложения

Хотя графы Петерсена известны с 1898 года, их определение как «нечётные графы» датируется работой Ковалевски, в которой он изучает нечётный граф O₄. Нечётные графы изучаются ввиду их использования в химической теории графов при моделировании сдвига ионов углерода. Они также используются в качестве сетевой топологии при параллельных вычислениях.

Обозначение O_n для этих графов предложено Норманом Биггсом в 1972 году. Биггс и Тони Гардинер объясняют название нечётных графов в неопубликованной монографии 1974 года — каждому ребру нечётного графа можно сопоставить единственный элемент X, который является «odd man out» (что можно перевести как «игрок без партнёра выходит из игры»), то есть элемент не принадлежит ни одному другому подмножеству, связанному с вершинами, инцидентными данному ребру.

Свойства

Нечётный граф O_n является регулярным графом степени n. Он имеет ${\tbinom {2n-1}{n-1}}$ вершин и $n{\tbinom {2n-1}{n-1}}/2$ рёбер. Таким образом, число вершин для n = 1, 2,… будет

1, 3, 10, 35, 126, 462, 1716, 6435 (последовательность A001700 в OEIS).

Дистанция и симметрия

Если две вершины в O_n соответствуют множествам одинакового размера, отличающихся k элементами, то можно получить из первого второе за 2k шагов, на каждом шаге убирая или добавляя один элемент. Если 2k < n, то это кратчайший путь. В противном случае можно найти более короткий путь этого типа, если начать с дополнительного ко второму множества, а затем получить второе множество, сделав ещё один шаг. Таким образом, диаметр графа O_n равен n − 1.

Любой нечётный граф 3-дужно-транзитивен — любой ориентированный трёхрёберный путь в нечётном графе может быть переведён в любой такой же путь с помощью симметрии графа. Нечётные графы дистанционно-транзитивны, поскольку они дистанционно-регулярны. Как дистанционно-регулярные графы, они однозначно определяются их массивом пересечений — никакой другой дистанционно-регулярный граф не может иметь те же самые параметры, что и нечётный граф. Однако вопреки высокой степени симметрии, нечётные графы O_n для n > 2 никогда не являются Графами Кэли.

Нечётные графы с n ≥ 3 имеют обхват шесть. Однако, хотя они и не являются двудольными графами, их нечётные циклы намного длиннее, а именно нечётный граф O_n имеет нечётный обхват 2n − 1. Если n-регулярный граф имеет диаметр n − 1, нечётный обхват 2n − 1 и только n различных собственных значений, он должен быть дистанционно-регулярным. Дистанционно-регулярные графы диаметра n − 1 и нечётного обхвата 2n − 1 известны как обобщённые нечётные графы и включают складные кубические графы так же, как и сами нечётные графы.

Независимые множества и раскраска вершин

Пусть O_n — нечётный граф, определённый на (2n − 1)-элементных подмножествах множества X, и пусть x — элементы множества X. Тогда среди вершин O_n ровно ${\tbinom {2n-2}{n-2}}$ вершин соответствуют множествам, которые содержат x. Поскольку все эти множества содержат x, они не являются непересекающимися, и образуют независимое множество графа O_n. Таким образом, O_n имеет 2n − 1 различных независимых множеств размера ${\tbinom {2n-2}{n-2}}$. Из теоремы Эрдёша – Ко – Радо следует, что это максимальные независимые множеств графа O_n. Таким образом, число независимости графа O_n равно ${\tbinom {2n-2}{n-2}}.$ Более того, любое максимальное независимое множество должно иметь этот вид, так что O_n имеет в точности 2n − 1 максимальных независимых множеств.

Если I — максимальное независимое множество, образованное множеством содержащим элемент x, то дополнение множества I — это множество вершин, не содержащих x. Это дополнение порождает паросочетание в G. Каждая вершина независимого множества смежна n вершинам паросочетания, а каждая вершина паросочетания смежна n − 1 вершинам независимого множества. Ввиду этого разложения и ввиду того, что нечётные графы не являются двудольными, они имеют хроматическое число равное трём — вершинам максимального независимого множества можно назначить один цвет, а два других цвета получим из паросочетания, порождённого дополнением.

Рёберная раскраска

По теореме Визинга число цветов, необходимых для раскраски рёбер нечётного графа O_n, равно либо n, либо n + 1, и в случае графов Петерсена O₃ оно равно n + 1. Если n — степень двух, число вершин в графе нечётно, откуда опять следует, что число цветов в рёберной раскраске равно n + 1. Однако O₅, O₆ и O₇ могут быт раскрашены n цветами.

Биггс объясняет эту задачу следующей историей: одиннадцать футболистов в придуманном городе Кроам хотят образовать пары команд для мини-футбола (один человек остаётся судить встречу) всеми 1386 различными способами и хотят составить расписание игр между всеми парами, при этом шесть игр каждой команды должны играться в разные дни недели, при отсутствии игр по воскресеньям. Возможно ли это? В этой истории каждая игра представляет ребро O₆, все дни представлены цветами, а рёберная раскраска в 6 цветов графа O₆ даёт расписание.

Нечётные графы и гамильтоновы графы

Граф Петерсена O₃ — это хорошо известные негамильтоновы графы, но было показано, что графы от O₄ до O₁₄ содержат гамильтоновы циклы. Более строго, комбинируя задачи поиска гамильтоновых циклов и рёберной раскраски, можно разбить рёбра графа O_n (для n = 4, 5, 6, 7) на ближайшее снизу целое от (n/2) гамильтоновых циклов. Если n нечётно, оставшиеся рёбра образуют совершенное сочетание. Для n = 8, нечётное число вершин в O_n не позволяет раскрасить рёбра в 8 цветов, но не закрывает возможность разложения на четыре гамильтоновых цикла.

Гипотеза Ловаса о гамильтоновом цикле предполагает, что каждый нечётный граф имеет гамильтонов путь и что каждый нечётный граф O_n с n ≥ 4 имеет гамильтонов цикл.

Литература

• Norman Biggs. Second International Conference on Combinatorial Mathematics. — 1979. — Т. 319. — С. 71—81. — doi:10.1111/j.1749-6632.1979.tb32775.x.