Нотация Конвея для многогранников

Этот рисунок показывает 11 новых многогранников, которые можно получить из куба с помощью трёх операций. Новые многогранники показаны как отображения на поверхность куба, чтобы были яснее видны топологические изменения. Вершины на всех многогранниках изображены в виде кружочков.

Н рисунке добавлены 3 другие операции — операция p=propellor Джорджа Харта, добавляющая четырёхугольники, операция g=gyro , создающая пятиугольники и операция c=chamfer, заменяющая рёбра шестиугольниками

Нотация Конвея для многогранников, разработанная Конвеем и продвигаемая Хартом, используется для описания многогранников, опираясь на затравочный (т.е. используемый для создания других) многогранник, модифицируемый различными префикс-операциями.

Конвей и Харт расширили идею использования операторов, подобных оператору truncation (усечения), определённого Кеплером, чтобы создавать связанные многогранники с той же симметрией. Базовые операторы могут сгенерировать все архимедовы тела и каталановы тела из правильных затравок. Например, tC представляет усечённый куб, а taC, полученный как t(aC), является усечённым октаэдром. Простейший оператор dual (двойственный) меняет местами вершины и грани. Так, двойственным многогранником для куба является октаэдр — dC=O. Применённые последовательно, эти операторы позволяют сгенерировать многие многогранники высокого порядка. Получающиеся многогранники будут иметь фиксированную топологию (вершины, рёбра, грани), в то время как точная геометрия не ограничивается.

Затравочные многогранники, являющиеся правильными многогранниками, представляются первой буквой в их (английском) названии (Tetrahedron = тетраэдр, Octahedron = октаэдр, Cube = куб, Icosahedron = икосаэдр, Dodecahedron = додекаэдр). Кроме того, используются призмы (Pn – от prism для n-угольных призм), антипризмы (An – от Antiprisms), купола (Un – от cupolae), антикупола (Vn) и пирамиды (Yn – от pyramid). Любой многогранник может выступать в качестве затравки, если операции могут на них быть выполнены. Например, правильногранные многогранники можно обозначить как Jn (от Johnson solids = тела Джонсона) для n=1…92.

В общем случае трудно предсказать результат последовательного применения двух и более операций на заданный многогранник-затравку. Например, операция ambo, применённая дважды, оказывается той же самой, что и операция expand (расширения), aa=e, в то время как операция truncation (усечение) после операции ambo даёт то же, что и операция bevel, ta=b. Не существует общей теории, описывающей, какие многогранники могут быть получены с помощью некоторого набора операторов. Наоборот, все результаты были получены эмпирически.

Операции на многогранниках

Элементы таблицы даны для затравки с параметрами (v,e,f) (вершин, рёбер, граней), преобразуемой в новые виды в предположении, что затравка является выпуклым многогранником (топологической сферой с эйлеровой характеристикой 2). Пример, базирующийся на затравке в виде куба, дан для каждого оператора. Базовые операции достаточны для генерации зеркально симметричных однородных многогранников и их двойственных. Некоторые базовые операции можно выразить через композицию других операций.

Специальные виды

Операция «kis» имеет вариант kn, в этом случае добавляются только пирамиды к граням с n-сторонами.

Операция усечения имеет вариант tn, в этом случае усекаются только вершины порядка n.

Операторы применяются подобно функциям справа налево. Например, кубооктаэдр является ambo кубом (кубом, к которому применена операция ambo), то есть t(C) = aC, а усечённый кубооктаэдр равен t(a(C)) = t(aC) = taC.

Оператор хиральности

• r – «отражение» («reflect») – делает зеркальное отражение затравки. Оператор не меняет затравку, если к ней не были применены операторы s или g. Другой записью хиральной формы служит надчёркивание, например, s = rs.

Операции в таблице показаны на примере куба и нарисованы на поверхности куба. Синие грани пересекают исходные рёбра, розовые грани соответствуют исходным вершинам.

Базовые операции

Оператор	Пример	Название	Альтернативное построение	вершины	рёбра	грани	Описание
		Затравка		v	e	f	Исходный многогранник
r		reflect		v	e	f	Зеркальный образ для хиральных форм
d		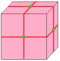dual		f	e	v	Двойственный многогранник для затравки – каждая вершина создаёт новую грань
a		ambo	dj djd	e	2e	f+v	Новые вершины добавляются в середине рёбер, а старые вершины отрезаются (rectify) Операция создаёт вершины с валентностью 4.
j		join	da dad	v+f	2e	e	К затравке добавляются пирамиды с достаточной высотой, так что два треугольника, принадлежащие разным пирамидам и имеющие общую сторону затравки, становятся копланарными (лежащими на одной плоскости) и образуют новую грань. Операция создаёт квадратные грани.
k kn		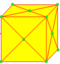kis	nd = dz dtd	v+f	3e	2e	На каждой грани добавляется пирамида. Акизация или кумуляция, увеличение или пирамидальное расширение.
t tn		truncate	nd = dz dkd	2e	3e	v+f	Отсекает все вершины. Операция является сопряжённой с kis
n		needle	kd = dt dzd	v+f	3e	2e	Двойственный многогранник к усечённой затравке. Грани триангулируются с двумя треугольниками для каждого ребра. Это делит пополам грани через все вершины и рёбра, удаляя при этом исходные рёбра. Операция преобразует геодезический многогранник (a,b) в (a+2b,a-b) для a>b. Она также преобразует (a,0) в (a,a), (a,a) в (3a,0), (2,1) в (4,1), и т.д.
z		zip	dk = td dnd	2e	3e	v+f	Двойственный многогранник к затравке после операции kis или усечение двойственного многогранника. Операция создаёт новые рёбра, перпендикулярные исходным рёбрам. Операция также называется bitruncation (глубоким усечением). Эта операция преобразует многогранник Голдберга G(a,b) в G(a+2b,a-b) для a>b. Она также преобразует G(a,0) в G(a,a), G(a,a) в G(3a,0), G(2,1) в G(4,1) и т.д.
e		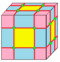expand (растяжение)	aa dod = do	2e	4e	v+e+f	Каждая вершина создаёт новую грань, а каждое ребро создаёт новый четырёхугольник. (cantellate = скашивание)
o		ortho	daa ded = de	v+e+f	4e	2e	Каждая n-угольная грань делится на n четырёхугольников.
g rg=g		gyro	dsd = ds	v+2e+f	5e	2e	Каждая n-угольная грань делится на n пятиугольников.
s rs=s		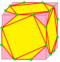snub	dgd = dg	2e	5e	v+2e+f	«расширение и кручение» – каждая вершина образует новую грань, а каждое ребро образует два новых треугольника
b		bevel	dkda = ta dmd = dm	4e	6e	v+e+f	Новые грани добавляются вместо рёбер и вершин. (cantitruncation = скос-усечение)
m		meta medial	kda = kj dbd = db	v+e+f	6e	4e	Триангуляция с добавлением вершин в центрах граней и рёбер.

Образование правильных затравок

Все пять правильных многогранников могут быть получены из призматических генераторов, используя от нуля до двух операторов:

• Треугольная пирамида: Y3 (Тетраэдр является частным случаем пирамид)
  • T = Y3
  • O = aT (тетраэдр после операции ambo)
  • C = jT (тетраэдр после операции join)
  • I = sT (плосконосый тетраэдр, тетраэдр после операции snub)
  • D = gT (тетраэдр после операции gyro)
• Треугольная антипризма: A3 (Октаэдр является частным случаем антипризм)
  • O = A3
  • C = dA3
• Квадратная призма: P4 (Куб является частным случаем призмы)
  • C = P4
• Пятиугольная антипризма: A5
  • I = k5A5 (Частный случай скрученно удлинённой бипирамиды)
  • D = t5dA5 (Частный случай усечённого трапецоэдра)

Правильная евклидова мозаика может также быть использована в качестве затравки:

• Q = Quadrille (четырёхугольная мозаика) = квадратная мозаика
• H = Hextille = шестиугольная мозаика = dΔ
• Δ = Deltille = треугольная мозаика = dH

Примеры

Куб может образовать все выпуклые однородные многогранники с октаэдральной симметрией. В первой строке показаны архимедовы тела, а во второй — каталановы тела. Вторая строка образуется как двойственные многогранники к многогранникам первой строки. Если сравнивать каждый новый многогранник с кубом, можно понять визуально проведённые операции.

Куб «затравка»	ambo	truncate	zip	expand	bevel	snub
C dO	aC aO	tC zO	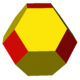zC = dkC tO	aaC = eC eO	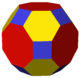bC = taC taO	sC sO
dual	join	needle	kis	ortho	medial	gyro
dC O	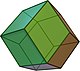jC jO	dtC = kdC kO	kC dtO	oC oO	dtaC = mC mO	gC gO

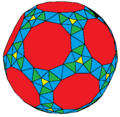
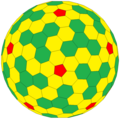
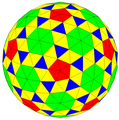
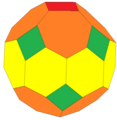
Усечённый икосаэдр, tI или zD, являющийся многогранником Голдберга G(2,0), создаёт дополнительные многогранники, которые ни вершинно-, ни гранетранзитивны.

Усечённый икосаэдр в качестве затравки

«затравка»	ambo	truncate	zip	extension	bevel	snub
zD tI Архивная копия от 21 октября 2016 на Wayback Machine	azI atI Архивная копия от 1 февраля 2017 на Wayback Machine	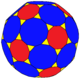tzD ttI Архивная копия от 1 февраля 2017 на Wayback Machine	tdzD tdtI Архивная копия от 21 октября 2016 на Wayback Machine	aazD = ezD aatI = etI Архивная копия от 1 февраля 2017 на Wayback Machine	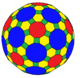bzD btI Архивная копия от 1 февраля 2017 на Wayback Machine	szD stI Архивная копия от 1 февраля 2017 на Wayback Machine
dual	join	needle	kis	ortho	medial	gyro
dzD dtI Архивная копия от 1 февраля 2017 на Wayback Machine	jzD jtI Архивная копия от 1 февраля 2017 на Wayback Machine	kdzD kdtI Архивная копия от 1 февраля 2017 на Wayback Machine	kzD ktI Архивная копия от 1 февраля 2017 на Wayback Machine	ozD otI Архивная копия от 1 февраля 2017 на Wayback Machine	mzD mtI Архивная копия от 1 февраля 2017 на Wayback Machine	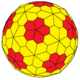gzD gtI Архивная копия от 1 февраля 2017 на Wayback Machine

Геометрические координаты производных форм

В общем случае затравка может считаться замощением поверхности. Поскольку операторы представляют топологические операции, то точные положения вершин производных форм в общем случае не определены. Выпуклые правильные многогранники в качестве затравки могут рассматриваться как замощения сферы, а потому производные многогранники можно рассматривать как расположенные на сфере. Подобно правильным мозаикам на плоскости, таким как шестиугольный паркет, эти многогранники на сфере могут выступать в качестве затравки для производных мозаик. Невыпуклые многогранники могут стать затравками, если связанные топологические поверхности определяются для ограничения положения вершин. Например, тороидальные многогранники могут произвести другие многогранники с точками на той же торической поверхности.

Пример: Затравка в виде додекаэдра как сферическая мозаика

D	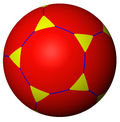tD	aD	zD = dkD	eD	bD = taD	sD
dD	nD = dtD	jD = daD	kD = dtdD	oD = deD	mD = dtaD	gD

Пример: Затравка в виде евклидовой шестиугольной мозаики (H)

H	tH	aH	tdH = H	eH	bH = taH	sH
dH	nH = dtH	jH = daH	dtdH = kH	oH = deH	mH = dtaH	gH = dsH

Производные операции

Смешение двух и более базовых операций приводит к широкому разнообразию форм. Имеется много других производных операций. Например, смешение двух ambo, kis или expand операций вместе с операциями dual. Использование альтернативных операторов наподобие join, truncate, ortho, bevel и medial может упростить имена и удалить операторы dual. Общее число рёбер производных операций можно вычислить через мультипликаторы каждого отдельного оператора.

Оператор(ы)	d	a j	k, t n, z	e o	g s	a&k	a&e	k&k	k&e k&a2	e&e
рёберный мультипликатор	1	2	3	4	5	6	8	9	12	16
Уникальных производных операторов						8	2	8	10	2

Операции в таблице показаны для куба (в качестве примера затравки) и нарисованы на поверхности куба. Голубые грани пересекают исходные рёбра, а розовые грани соответствуют исходным вершинам.

Производные операции

Оператор	Пример	Название	Альтернативное построение	вершины	рёбра	грани	Описание
		Затравка		v	e	f	Исходный многогранник
at			akd	3e	6e	v+2e+f	Операция ambo после truncate
jk			dak	v+2e+f	6e	3e	Операция join после kis. Подобна ortho, за исключением того, что новые квадратные грани вставляются на место исходных рёбер
ak		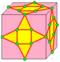	dajd	3e	6e	v+2e+f	Операция ambo после kis. Подобна expand, за исключением того, что новые вершины добавляются на исходные рёбра, образуя два треугольника.
jt			dakd = dat	v+2e+f	6e	3e	Операция join после truncate. Двойственный многогранник к полученному после операций truncate, затем ambo
tj		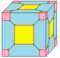	dka	4e	6e	v+e+f	truncate join
ka				v+e+f	6e	4e	kis ambo
ea or ae		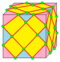	aaa	4e	8e	v+3e+f	расширенная операция ambo, тройная операция ambo
oa or je		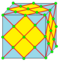	daaa = jjj	v+3e+f	8e	4e	Операция ortho после ambo, тройная операция join
x=kt		exalt	kdkd dtkd	v+e+f	9e	7e	Операции kis truncate, триангуляция, деление рёбер на 3 части и добавление новых вершин в центр исходных граней. Операция преобразует геодезический многогранник (a,b) в (3a,3b).
y=tk		yank	dkdk dktd	v+e+f	9e	7e	Операции truncate kis, расширение шестиугольниками вокруг каждого ребра Операция преобразует многогранник Голдберга G(a,b) в G(3a,3b).
nk			kdk = dtk = ktd	7e	9e	v+e+f	needled kis
tn			dkdkd = dkt = tkd	7e	9e	v+e+f	truncate needle
tt			dkkd	7e	9e	v+e+f	двойная операция truncate
kk			dttd	v+2e+f	9e	6e	двойная операция kis
nt			kkd = dtt	v+e+f	9e	7e	needle truncate
tz			dkk = ttd	6e	9e	v+2e+f	truncate zip
ke			kaa	v+3e+f	12e	8e	Kis expand
to			dkaa	8e	12e	v+3e+f	truncate ortho
ek			aak	6e	12e	v+5e+f	expand kis
ok			daak = dek	v+5e+f	12e	6e	ortho kis
et			aadkd	6e	12e	v+5e+f	расширенная операция truncate
ot			daadkd = det	v+5e+f	12e	6e	ortho truncate
te or ba			dkdaa	8e	12e	v+3e+f	truncate expand
ko or ma			kdaa = dte ma = mj	v+3e+f	12e	8e	kis ortho
ab or am			aka = ata	6e	12e	v+5e+f	ambo bevel
jb or jm		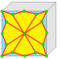	daka = data	v+5e+f	12e	6e	joined bevel
ee			aaaa	v+7e+f	16e	8e	double-expand
oo			daaaa = dee	8e	16e	v+7e+f	double-ortho

Хиральные производные операции

Имеются другие производные операции, если используется gyro с операциями ambo, kis или expand и до трёх операций dual.

Оператор(ы)	d	a	k	e	g	a&g	k&g	e&g	g&g
мультипликатор рёбер	1	2	3	4	5	10	15	20	25
Уникальных производных операторов						4	8	4	2

Хиральные порождённые операции

Оператор	Пример	Название	Построение	вершин	рёбер	граней	Описание
		Затравка		v	e	f	Исходный многогранник
ag			as djsd = djs	v+4e+f	10e	5e	ambo gyro
jg			dag = js dasd = das	5e	10e	v+4e+f	joined gyro
ga			gj dsjd = dsj	v+5e+f	10e	4e	gyro ambo
sa			dga = sj dgjd = dgj	4e	10e	v+5e+f	snub ambo
kg			dtsd = dts	v+4e+f	15e	10e	kis gyro
ts			dkgd = dkg	10e	15e	v+4e+f	truncated snub
gk			dstd	v+8e+f	15e	6e	gyro kis
st			dgkd	6e	15e	v+8e+f	snub truncation
sk			dgtd	v+8e+f	15e	6e	snub kis
gt			dskd	6e	15e	v+8e+f	gyro truncation
ks			kdg dtgd = dtg	v+4e+f	15e	10e	kis snub
tg			dkdg dksd	10e	15e	v+4e+f	truncated gyro
eg			es aag	v+9e+f	20e	10e	expanded gyro
og			os daagd = daag	10e	20e	v+9e+f	expanded snub
ge			go gaa	v+11e+f	20e	8e	gyro expand
se			so dgaad = dgaa	8e	20e	v+11e+f	snub expand
gg			gs dssd = dss	v+14e+f	25e	10e	double-gyro
ss			sg dggd = dgg	10e	25e	v+14e+f	double-snub

Расширенные операторы

Эти расширенные операторы нельзя создать в общем виде с помощью выше перечисленных базовых операций. Некоторые операторы могут быть созданы как частные случаи с k и t операторами, но применённые к определённым граням и вершинам. Например, куб со снятой фаской, cC, может быть построен как t4daC, как ромбододекаэдр, daC или jC с усечёнными вершинами валентности 4. Поднятый куб lC — это то же самое, что t4kC, квинтододекаэдр qD можно построить как t5daaD, t5deD или t5oD, a дельтоидальный гексеконтаэдр можно построить как deD или oD с усечением вершин с валентностью 5.

Некоторые расширенные операторы образуют последовательность и даны с последующим числом. Например, ortho делит квадратную грань на 4 квадрата, а o3 может делить на 9 квадратов. o3 является уникальным построением, в то время как o4 можно получить как oo, оператор ortho, применённый дважды. Оператор loft может включать индекс подобно оператору kis, чтобы ограничить применение на грани с указанным числом сторон.

Операция chamfer (снятие фаски) создаёт многогранник Голдберга G(2,0) с новыми шестиугольниками между исходными гранями. Последовательные операции chamfer создают G(2n,0).

Расширенные операции

Оператор	Пример	Название	Альтернативное построение	вершин	рёбер	граней	Описание
		Затравка		v	e	f	Исходный многогранник
c (от chamfer)		chamfer	dud	v + 2e	4e	f + e	Усечение рёбер. Вместо рёбер вставляются новые шестиугольные грани. Многогранник Голдберга (0,2)
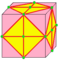-		-	dc	f + e	4e	v + 2e	Операция dual после chamfer
u		subdivide	dcd	v+e	4e	f+2e	Операция ambo, пока сохраняются исходные вершины Операция аналогична cхеме Лупа подразделения поверхности для треугольных граней
-			cd	f+2e	4e	v+e	Операция dual после subdivide
l ln		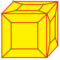loft		v+2e	5e	f+2e	Расширение каждой грани призмой, добавление меньшей копии каждой грани с трапециями между внутренней и внешней гранью.
			dl dln	f+2e	5e	v+2e	Операция dual после loft
			ld lnd	f+2e	5e	v+2e	Операция loft после dual
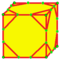			dld dlnd	v+2e	5e	f+2e	Операция, сопряжённая с loft
			dL0	f+3e	6e	v+2e	Операция dual после joined-lace
			L0d	f+2e	6e	v+3e	Операция joined-lace после dual
			dL0d	v+3e	6e	f+2e	Операция, сопряжённая с joined-lace
q		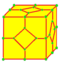quinto		v+3e	6e	f+2e	Операция ortho с последующим усечением вершин, находящихся в центре исходных граней. Операция создаёт 2 новых пятиугольника для каждого исходного ребра.
-			dq	f+2e	6e	v+3e	Операция dual после quinto
			qd	v+2e	6e	f+3e	Операция quinto после dual
-			dqd	f+3e	6e	v+2e	Операция, сопряжённая с quinto
L0		joined-lace		v+2e	6e	f+3e	Аналогична операции lace, но с новыми четырёхугольными гранями на месте исходных рёбер
L Ln		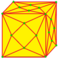Lace		v+2e	7e	f+4e	Расширение каждой грани антипризмой, добавление повёрнутой меньшей копии каждой грани с треугольниками между старой и новой гранями. Индекс может быть добавлен для ограничения операции на грани с указанным числом сторон.
			dL dLn	f+4e	7e	v+2e	Оператор dual после laced
			Ld Ldn	f+2e	7e	v+4e	Оператор lace после dual
			dLd dLnd	v+4e	7e	f+2e	Последовательность операций dual, lace, dual
K Kn		staKe		v+2e+f	7e	4e	Подразделение граней с центральными чётырёхугольниками и треугольниками. Может быть добавлен индекс для ограничения операции на грани с определённым числом сторон.
			dK dKn	4e	7e	v+2e+f	Операция dual после stake
			Kd	v+2e+f	7e	4e	Операция stake после dual
			dKd	4e	7e	v+2e+f	Операция, сопряжённая со stake
M3		edge-medial-3		v+2e+f	7e	4e	Операция подобна m3, но не добавляются диагональные рёбра
			dM3	4e	7e	v+2e+f	Операция dual после edge-medial-3
			M3d	v+2e+f	7e	4e	Операция edge-medial-3 после dual
			dM3d	4e	7e	v+2e+f	Операция, сопряжённая с edge-medial-3
M0		joined-medial		v+2e+f	8e	5e	Операция подобна medial, но с добавлением ромбических граней на месте исходных рёбер.
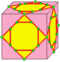			dM0	v+2e+f	8e	5e	Операция dual после joined-medial
			M0d	v+2e+f	8e	5e	Операция joined-medial после dual
			dM0d	5e	8e	v+2e+f	Операция, сопряжённая с joined-medial
m3		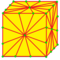medial-3		v+2e+f	9e	7e	Триангуляция с добавлением двух вершин на каждое ребро и одной вершины в центре каждой грани.
b3		bevel-3	dm3	7e	9e	v+2e+f	Операция dual после medial-3
			m3d	7e	9e	v+2e+f	Операция medial-3 после dual
			dm3d	v+2e+f	9e	7e	Операция, сопряжённая с medial-3
o3		ortho-3	de3	v+4e	9e	f+4e	Оператор ortho с делением рёбер на 3
e3		expand-3	do3	f+4e	9e	v+4e	Оператор expand с делением рёбер на 3
X		cross		v+f+3e	10e	6e	Комбинация операций kis и subdivide. Исходные рёбра делятся пополам и образуются треугольные и четырёхугольные грани.
			dX	6e	10e	v+f+3e	Операция dual после cross
			Xd	6e	10e	v+f+3e	Операция cross после dual
			dXd	v+f+3e	10e	6e	Операция, сопряжённая с cross
m4		medial-4		v+3e+f	12e	8e	Триангуляция с добавлением 3 вершин на каждое ребро и вершины в центр каждой грани.
u5		subdivide-5		v+8e	25e	f+16e	Рёбра делятся на 5 частей Этот оператор делит рёбра и грани так, что образуется 6 треугольников вокруг каждой новой вершины.

Расширенные хиральные операторы

Эти операторы нельзя создать в общем виде из перечисленных выше базовых операций. Художник-геометр Харт создал операцию, которую он назвал пропеллер.

• p – «propeller» = пропеллер (оператор вращения, создающий четырёхугольники на месте вершин). Эта операция самодвойственна: dpX=pdX.

Расширенные хиральные операции

Оператор	Пример	Название	Альтернативное построение	вершины	рёбра	грани	Описание
		«Затравка»		v	e	f	Исходный многогранник
p rp=p		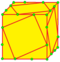propellor		v + 2e	5e	f + 2e	Операция gyro, после которой выполняется ambo на вершинах в центрах исходных граней
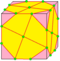-		-	dp = pd	f + 2e	5e	v + 2e	Те же вершины, что и в gyro, но на месте исходных вершин образуются грани
-				4e	7e	v+2e+f	Операция подобна snub, но по периметру исходных граней идут пятиугольники, а не треугольники
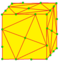-		-	-	v+2e+f	7e	4e
w=w2=w2,1 rw=w		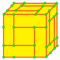whirl		v+4e	7e	f+2e	Операция gyro с последующим усечением вершин в центре исходных граней. Операция создаёт 2 новых шестиугольника для каждого исходного ребра, многогранник Голдберга (2,1) Производный оператор wrw преобразует G(a,b) в G(7a,7b).
v rv=v		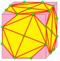volute	dwd	f+2e	7e	v+4e	Оператор dual после whirl, или snub с последующей операцией kis на исходных гранях. Полученный оператор vrv преобразует геодезический многогранник (a,b) в (7a,7b).
g3 rg3=g3		gyro-3		v+6e	11e	f+4e	Операция gyro создаёт 3 пятиугольника вдоль каждого исходного ребра
s3 rs3=s3		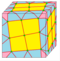snub-3	dg3d = dg3	f+4e	11e	v+6e	Операция dual после gyro-3, операция snub, делящая рёбра на 4 срединных треугольника и с треугольниками на месте исходных вершин
w3,1 rw3,1=w3,1		whirl-3,1		v+8e	13e	f+4e	Операция создаёт 4 новых шестиугольника для каждого исходного ребра, многогранник Голдберга (3,1)
w3=w3,2 rw3=w3		whirl-3,2		v+12e	19e	f+6e	Операция создаёт 12 новых шестиугольников для каждого исходного ребра, многогранник Голдберга (3,2)

Операции, сохраняющие исходные рёбра

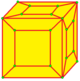
Эти операции расширения оставляют исходные рёбра и позволяют применять оператор к любому независимому подмножеству граней. Нотация Конвея поддерживает дополнительный индекс для этих операций, указывающий число сторон у вовлечённых в операцию граней.

Оператор	kis	cup	acup	loft	lace	stake	kis-kis
Пример	kC	UC	VC	lC	LC	KC	kkC
Рёбра	3e	4e-f4	5e-f4	5e	6e	7e	9e
Изображение на кубе
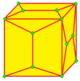Расширение	Пирамида	Купол	Антикупол	Призма	Антипризма

Операторы Коксетера

Операторы Коксетера/Джонсона иногда полезны при смешении с операторами Конвея. Для ясности в нотации Конвея эти операции даны заглавными буквами. t-Нотация Коксетера определяет активные кружки как индексы диаграммы Коксетера — Дынкина. Таким образом, в таблице заглавная T с индексами 0,1,2 определяет однородные операторы из правильной затравки. Нулевой индекс представляет вершины, 1 представляет рёбра, а 2 представляет грани. При T = T_0,1 это будет обычным усечением, а R = T₁ является полным усечением, или операцией rectify, то же самое, что и оператор Конвея ambo. Например, r{4,3} или t₁{4,3} является именем Коксетера для кубооктаэдра, а полноусечённый куб — это RC, то же самое, что ambo куб Конвея, aC.

Расширенные операции Коксетера

Оператор	Пример	Название	Альтернативное построение	вершины	рёбра	грани	Описание
T0	, t0{4,3}	«Затравка»		v	e	f	Seed form
R = T1	, t1{4,3}	rectify	a	e	2e	f+v	То же самое, что ambo, новые вершины добавляются в середине рёбер, а новые грани заменяют исходные вершины. Все вершины имеют валентность 4.
T2	, t2{4,3}	dual birectify	d	f	e	v	Операция dual для затравочного многогранника — каждая вершина создаёт новую грань
T = T0,1	, t0,1{4,3}	truncate	t	2e	3e	v+f	Отсекаются все вершины.
T1,2	, t1,2{4,3}	bitruncate	z = td	2e	3e	v+f	То же самое, что и zip
RR = T0,2	, t0,2{4,3}	cantellate	aa=e	2e	4e	v+e+f	То же самое, что и expand
TR = T0,1,2	, t0,1,2{4,3}	cantitruncate	ta	4e	6e	v+e+f	То же самое, что и bevel

Полуоператоры

плосконосый куб строится как одно из двух альтернирований усечённого кубооктаэдра. sr{4,3} = SRC = HTRC.

Многогранники F1bC и F2bC не идентичны и могут сохранять в общем случае полную октаэдральную симметрию.

Оператор semi или demi Коксетера, H (от Half), уменьшает число сторон каждой грани вдвое, а четырёхугольные грани в двуугольники с двумя рёбрами, соединяющими две вершины, и эти два ребра могут быть заменены или не заменены одним ребром. Например, половинка куба, h{4,3}, полукуб, — это HC, представляющий один из двух тетраэдров. Ho сокращает ortho в ambo/Rectify.

Другие semi-операторы (полуоператоры) можно определить с использованием оператора H. Конвей называет оператор Snub (плосконосое усечение) Коксетера S, semi-snub (полуплосконосым усечением), определённым как Ht. Оператор snub s Конвея определяется как SR. Например, SRC — это плосконосый куб, sr{4,3}. Плосконосый октаэдр Коксетера, s{3,4} можно определить как SO, построение пиритоэдральной симметрии для правильного икосаэдра. Это также согласуется с определением правильной плосконосой квадратной антипризмой как SA4.

Оператор semi-gyro, G, определяется как dHt. Это позволяет определить оператор поворачивания Конвея g (gyro) как GR. Например, GRC — это gyro-куб, gC, или пентагональный икоситетраэдр. GO определяет пиритоэдр с пиритоэдральной симметрией, в то время как gT (gyro tetrahedron, гиротетраэдр) определяет тот же самый топологический многогранник с тетраэдральной симметрией.

Оба оператора S и G требуют, чтобы затравочный многогранник имел вершины чётной валентности. Во всех этих полуоператорах имеется два выбора для альтернации вершин для оператора half. Эти две конструкции в общем случае топологически не тождественны. Например, HjC определяет либо куб, либо октаэдр, в зависимости от того, какой набор вершин выбирается.

Другие операторы применимы только к многогранникам с гранями, имеющими чётное число рёбер. Простейшим оператором является semi-join, который является сопряжённым с оператором half, dHd.

Оператор semi-ortho, F, сопряжён с semi-snub. Он добавляет вершину в центр грани и делит пополам все рёбра, но соединяет новыми рёбрами центр только с половиной рёбер, создавая тем самым новые шестиугольные грани. Исходные квадратные грани не требуют наличия центральной вершины, а требует только одно ребро через грань, создающее пару пятиугольников. Например, двенадцатигранник тетартоид может быть построен как FC.

Оператор semi-expand, E, определяется как Htd или Hz. Оператор создаёт треугольные грани. Например, EC создаёт построение с пироэдральной симметрией псевдоикосаэдра.

Полуоператоры на многогранниках с гранями, имеющими чётное число сторон

Оператор	Пример (Затравка — куб)	Название	Альтернативное построение	вершин	рёбер	граней	Описание
H = H1 H2		semi-ambo Half 1 и 2		v/2	e-f4	f-f4+v/2	Альтернирование, удаление половины вершин. Четырёхугольные грани (f4) редуцируются до одиночных рёбер.
I = I1 I2		semi-truncate 1 и 2		v/2+e	2e	f+v/2	Усекает каждую вторую вершину
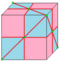		semi-needle 1 и 2	dI	v/2+f	2e	e+v/2	Операция needle каждой второй вершины
F = F1 F2		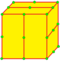semi-ortho Flex 1 и 2	dHtd = dHz dSd	v+e+f-f4	3e-f4	e	Операция dual после semi-expand — создаются новые вершины на рёбрах и в центрах граней, 2n-угольники делятся на n шестиугольников, четырёхугольные грани (f4) не будут содержать центральной вершины, так что образуется две пятиугольные грани.
E = E1 E2		semi-expand Eco 1 и 2	Htd = Hz dF = Sd dGd	e	3e-f4	v+e+f-f4	Операция dual после semi-ortho — создаются новые треугольные грани. Исходные грани заменяются многоугольниками с половиной сторон, четырёхугольники (f4) при этом редуцируются до одиночных рёбер.
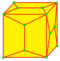U = U1 U2		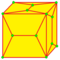semi-lace CUp 1 и 2		v+e	4e-f4	2e+f-f4	Наращение граней куполами.
V = V1 V2		semi-lace Anticup 3 и 4		v+e	5e-f4	3e+f-f4	Наращение граней антикуполами
		semi-medial 1 и 2	XdH = XJd	v+e+f	5e	3e	Поочерёдная операция medial относительно диагоналей
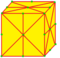		semi-medial 3 и 4		v+e+f	5e	3e	Поочерёдная операция medial относительно медиан (соединяющих середины противоположных сторон)
		semi-bevel 1 и 2	dXdH = dXJd	3e	5e	v+e+f	Поочерёдная операция bevel относительно диагоналей
		semi-bevel 3 и 4		3e	5e	v+e+f	Поочерёдная операция bevel относительно медиан

Полуоперации на многогранниках с вершинами чётной валентности

Оператор	Пример (Затравка — октаэдр)	Название	Альтернативное построение	вершин	рёбер	граней	Описание
J = J1 J2		semi-join 1 и 2	dHd	v-v4+f/2	e-v4	f/2	Оператор, сопряжённый с half, оператор join на чередующихся гранях. 4-валентные вершины (v4) редуцируются до 2-валентных и заменяются одним ребром.
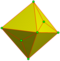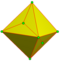		semi-kis 1 и 2	dId	v+f/2	2e	f/2+e	Операция kis на половине (поочерёдно, не соприкасающихся по ребру) граней
		semi-zip 1 и 2	Id	f/2+e	2e	v+f/2	Операция zip на половине граней
S = S1 S2		semi-snub 1 и 2	Ht dFd	v-v4+e	3e-v4	f+e	Операция dual после semi-gyro — операция snub, вращение исходных граней с добавлением новых треугольных граней в получающиеся зазоры.
G = G1 G2		semi-gyro 1 и 2	dHt dS = Fd dEd	f+e	3e-v4	v-v4+e	Операция dual после semi-snub — создаются пятиугольные и шестиугольные грани вдоль исходных рёбер.
		semi-medial 1 и 2	XdHd = XJ	3e	5e	v+e+f	Операция medial на половине (не соприкасающихся ребром) граней
		semi-bevel 1 и 2	dXdHd = dXJ	v+e+f	5e	3e	Операция bevel на половине (не соприкасающихся ребром) граней

Подразделения

Операция subdivision (подразделения) делит исходные рёбра на n новых рёбер, а внутренность граней заполняется треугольниками или другими многоугольниками.

Квадратное подразделение

Оператор ortho можно применить в серии степеней двойки четырёхугольных подразделений. Другие подразделения могут быть получены как результат факторизованных подразделений. Оператор propeller, применённый последовательно, даёт 5-орто подразделение. Если затравка имеет нечетырёхугольные грани, они остаются как уменьшенные копии для нечётных операторов ortho.

Примеры на кубе

Ortho		o2=o	o3	o4=o2	o5 =prp	o6=oo3	o7	o8=o3	o9=o32	o10=oo5 =oprp
Пример
Вершины	v	v+e+f	v+4e	v+7e+f	v+12e	v+17e+f	v+24e	v+31e+f	v+40e	v+63e+f
Рёбра	e	4e	9e	16e	25e	36e	49e	64e	81e	128e
Грани	f	2e	f+4e	8e	f+12e	18e	f+24e	32e	f+40e	64e
Expand (dual)		e2=e	e3	e4=e2	e5 =dprp	e6=ee3	e7	e8=e3	e9=e32	e10=ee5 =doprp
Пример

Хиральное шестиугольное подразделение

Оператор whirl создаёт многогранник Голдберга G(2,1) с новыми шестиугольными гранями вокруг каждой исходной вершины. Две последовательные операции whirls создают G(3,5). В общем случае операция whirl может преобразовать G(a,b) в G(a+3b,2a-b) для a>b и тем же самым хиральным направлением. Если хиральные направления обратны, G(a,b) превращается в G(2a+3b,a-2b) при a>=2b и в G(3a+b,2b-a) при a<2b.

Операторы whirl-n образуют многогранники Голдберга (n,n-1) и могут быть определены путём деления рёбер затравочного многогранника на 2n-1 подрёбер.

Результат операции whirl-n и ей обратной образует (3n²-3n+1,0) многогранник Голдберга. wrw образует (7,0), w₃rw₃ образует (19,0), w₄rw₄ образует (37,0), w₅rw₅ образует (61,0), а w₆rw₆ образует (91,0). Результат двух операций whirl-n — это ((n-1)(3n-1),2n-1) или (3n²-4n+1,2n-1). Произведение w_a на w_b даёт (3ab-2(a+b)+1,a+b-1), а w_a на обратный w_b даёт (3ab-a-2b+1,a-b) для a≥b.

Произведение двух идентичных операторов whirl-n образует многогранник Голдберга ((n-1)(3n-1),2n-1). Произведение k-whirl и zip — это (3k-2,1).

Операторы whirl-n

Название	Затравка	Whirl	Whirl-3	Whirl-4	Whirl-5	Whirl-6	Whirl-7	Whirl-8	Whirl-9	Whirl-10	Whirl-11	Whirl-12	Whirl-13	Whirl-14	Whirl-15	Whirl-16	Whirl-17	Whirl-18	Whirl-19	Whirl-20	Whirl-n
Оператор (Состоавной)	-	w=w2	w3	w4	w5	w6 wrw3,1	w7	w8 w3,1w3,1	w9 ww5,1	w10	w11	w12	w13 ww7,2	w14	w15	w16 ww9,2	w17 w3w6,1	w18	w19 w3,1w7,3	w20 ww11,3	wn
Многогранник Голдберга	(1,0)	(2,1)	(3,2)	(4,3)	(5,4)	(6,5)	(7,6)	(8,7)	(9,8)	(10,9)	(11,10)	(12,11)	(13,12)	(14,13)	(15,14)	(16,15)	(17,16)	(18,17)	(19,18)	(20,19)	(n,n-1)
T разложение	1	7	19	37	61	91 7×13	127	169 13×13	217 7×31	271	331	397	469 7×67	547	631	721 7×103	817 19×43	919	1027 13×79	1141 7×163	3n(n-1)+1
Пример
Вершина	v	v+4e	v+12e	v+24e	v+40e	v+60e	v+84e	v+112e	v+144e	v+180e	v+220e	v+264e	v+312e	v+364e	v+420e	v+480e	v+544e	v+612e	v+684e	v+760e	v+2n(n-1)e
Рёбра	e	7e	19e	37e	61e	91e	127e	169e	217e	271e	331e	397e	469e	547e	631e	721e	817e	919e	1027e	1141e	e+3n(n-1)e
Грани	f	f+2e	f+6e	f+12e	f+20e	f+30e	f+42e	f+56e	f+72e	f+90e	f+110e	f+132e	f+156e	f+182e	f+210e	f+240e	f+272e	f+306e	f+342e	f+380e	f+n(n-1)e
wnwn	(1,0)	(5,3)	(16,5)	(33,7)	(56,9)	(85,11)	(120,13)	(161,15)	(208,17)	(261,19)	(320,21)	(385,23)	(456,25)	(533,27)	(616,29)	(705,31)	(800,33)	(901,35)	(1008,37)	(1121,39)	((n-1)(3n-1),2n-1)
wnrwn	(1,0)	(7,0)	(19,0)	(37,0)	(61,0)	(91,0)	(127,0)	(169,0)	(217,0)	(271,0)	(331,0)	(397,0)	(469,0)	(547,0)	(631,0)	(721,0)	(817,0)	(919,0)	(1027,0)	(1141,0)	(1+3n(n-1),0)
wnz	(1,1)	(4,1)	(7,1)	(10,1)	(13,1)	(16,1)	(19,1)	(22,1)	(25,1)	(28,1)	(31,1)	(34,1)	(37,1)	(40,1)	(43,1)	(46,1)	(49,1)	(52,1)	(55,1)	(58,1)	(3n-2,1)

Триангулированное подразделение

Триангулированные подразделения u₁ to u₆ на квадратной грани, повторяя структуру через каждые 3 шага с новыми уровнями треугольников

Операция u_n делит грани на треугольники путём деления каждого ребра на n частей, называемой n-частотным подразделением геодезического многогранника Бакминстера Фуллера.

Операторы Конвея на многогранниках могут построить многие из этих подразделений.

Если все исходные грани являются треугольниками, новые многогранники будут также иметь все грани в виде треугольников, и на месте исходных граней создаются треугольные мозаики. Если исходные многогранники имеют грани с бо́льшим числом сторон, все новые грани не обязательно будут треугольниками. В таких случаях к многограннику сначала можно применить операцию kis с новыми вершинами в центре каждой грани.

Примеры подразделений на кубе

Оператор	u1	u2 =u	u3 =x	u4 =uu	u5	u6 =ux	u7 =vrv	u8 =uuu	u9 =xx
Пример
Обозначение Конвея	C Архивная копия от 2 февраля 2017 на Wayback Machine	uC Архивная копия от 15 марта 2017 на Wayback Machine	xC Архивная копия от 16 марта 2017 на Wayback Machine	uuC Архивная копия от 15 марта 2017 на Wayback Machine	u5C	uxC Архивная копия от 15 марта 2017 на Wayback Machine	vrvC Архивная копия от 15 марта 2017 на Wayback Machine	uuuC Архивная копия от 15 марта 2017 на Wayback Machine	xxC Архивная копия от 15 марта 2017 на Wayback Machine
Вершины	v	v+e	v+e+f	v+4e	v+8e	v+11e+f	v+16e	v+21e	v+26e+f
Рёбра	e	4e	9e	16e	25e	36e	49e	64e	81e
Грани	f	f+2e	7e	f+8e	f+16e	24e	f+32e	f+42e	54e
Полная триангуляция
Оператор	u1k	u2k =uk	u3k =xk	u4k =uuk	u5k	u6k =uxk	u7k =vrvk	u8k =uuuk	u9k =xxk
Пример
Конвей	kC Архивная копия от 5 февраля 2017 на Wayback Machine	ukC Архивная копия от 15 марта 2017 на Wayback Machine	xkC Архивная копия от 15 марта 2017 на Wayback Machine	uukC Архивная копия от 16 марта 2017 на Wayback Machine	u5kC	uxkC Архивная копия от 15 марта 2017 на Wayback Machine	vrvkC Архивная копия от 15 марта 2017 на Wayback Machine	uuukC Архивная копия от 16 марта 2017 на Wayback Machine	xxkC Архивная копия от 15 марта 2017 на Wayback Machine
Двойственный Голдберга	{3,n+}1,1	{3,n+}2,2	{3,n+}3,3	{3,n+}4,4	{3,n+}5,5	{3,n+}6,6	{3,n+}7,7	{3,n+}8,8	{3,n+}9,9

Геодезические многогранники

См. также: Геодезический многогранник и Многогранник Голдберга

Операции Конвея могут дублировать некоторые многогранники Голдберга и двойственные геодезическим многогранникам. Число вершин, рёбер и граней многогранника Голдберга G(m,n) можно вычислить исходя из m и n и число новых треугольников в каждом исходном треугольнике вычисляется по формуле T = m² + mn + n² = (m + n)² − mn. Построения (m,0) и (m,m) перечислены ниже обозначения операций Конвея.

Класс I

Для двойственных многогранников Голдберга оператор u_k определяется здесь как деление граней с подразделением рёбер на k частей. При этом оператор Конвея u = u₂, а его сопряжённый оператор dud является оператором chamfer, c. Этот оператор используется в компьютерной графике, в схеме Лупа подразделения поверхности. Оператор u₃ задаётся оператором Конвея kt=x, а его сопряжённый оператор y=dxd=tk. Произведение двух whirl операторов с обращением хиральности, wrw или ww, даёт 7-подразделение в виде многогранника Голдберга G(7,0), так что u₇=vrv. Более мелкие подразделения и операции whirl в хиральных парах могут построить дополнительные формы класса I. Операция w(3,1)rw(3,1) даёт многогранник Голдберга G(13,0). Операция w(3,2)rw(3,2) даёт G(19,0).

Class I: Операции подразделения на икосаэдре как геодезические многогранники

(m,0)	(1,0)	(2,0)	(3,0)	(4,0)	(5,0)	(6,0)	(7,0)	(8,0)	(9,0)	(10,0)	(11,0)	(12,0)	(13,0)	(14,0)	(15,0)	(16,0)
T	1	4	9	16	25	36	49	64	81	100	121	144	169	196	225	256
Операция Составной	u1	u2=u =dcd	u3=x =kt	u4 =u22 =dccd	u5	u6=u2u3 =dctkd	u7 =vv =dwrwd	u8=u23 =dcccd	u9=u32 =ktkt	u10=u2u5	u11	u12=u22u3 =dccdkt	u13 v3,1v3,1	u14=u2u7 =uvv =dcwrwd	u15= u3u5 =u5x	u16=u24 =dccccd
Треугольная грань
Икосаэдр Конвей Геодезический	I Архивная копия от 30 декабря 2016 на Wayback Machine {3,5+}1,0	uI=k5aI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}2,0	xI=ktI Архивная копия от 30 декабря 2016 на Wayback Machine {3,5+}3,0	u2I Архивная копия от 9 января 2017 на Wayback Machine {3,5+}4,0	{3,5+}5,0	uxI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}6,0	vrvI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}7,0	u3I Архивная копия от 9 января 2017 на Wayback Machine {3,5+}8,0	x2I Архивная копия от 8 января 2018 на Wayback Machine {3,5+}9,0	{3,5+}10,0	{3,5+}11,0	u2xI Архивная копия от 10 января 2017 на Wayback Machine {3,5+}12,0	{3,5+}13,0	uvrvI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}14,0	{3,5+}15,0	u4I Архивная копия от 9 января 2017 на Wayback Machine {3,5+}16,0
Двойственный оператор		c	y =tk	cc	c5	cy =ctk	ww =wrw	ccc	y2 =tktk	cc5	c11	ccy =cctk	w3,1w3,1	cww =cwrw	c5y	cccc
Додекаэдр Конвей Голдберг	D Архивная копия от 30 декабря 2016 на Wayback Machine {5+,3}1,0	cD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}2,0	yD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}3,0	ccD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}4,0	c3D {5+,3}5,0	cyD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}6,0	wrwD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}7,0	cccD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}8,0	y2D Архивная копия от 30 декабря 2016 на Wayback Machine {5+,3}9,0	cc5D {5+,3}10,0	c11D {5+,3}11,0	ccyD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}12,0	w3,1rw3,1D {5+,3}13,0	cwrwD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}14,0	c5yD {5+,3}15,0	ccccD Архивная копия от 9 января 2017 на Wayback Machine G{5+,3}16,0

Класс II

Может быть определено также ортогональное подразделение, используя оператор n=kd. Оператор преобразует геодезический многогранник (a,b) в (a+2b,a-b) для a>b. Он преобразует (a,0) в (a,a), а (a,a) в (3a,0). Оператор z=dk делает то же самое для многогранников Голдберга.

Класс II: Операции ортогонального подразделения

(m,m)	(1,1)	(2,2)	(3,3)	(4,4)	(5,5)	(6,6)	(7,7)	(8,8)	(9,9)	(10,10)	(11,11)	(12,12)	(13,13)	(14,14)	(15,15)	(16,16)
T= m2×3	3 1×3	12 4×3	27 3×3	48 24×3	75 25×3	108 36×3	147 49×3	192 64×3	243 81×3	300 100×3	363 121×3	432 144×3	507 169×3	588 196×3	675 225×3	768 256×3
Операция	u1n n =kd	u2n =un =dct	u3n =xn =ktkd	u4n =u22n =dcct	u5n	u6n =u2=u3n =dctkt	u7n =vvn =dwrwt	u8n =u23n =dccct	u9n =u32n =ktktkd	u10n =u2u5n	u11n	u12n =u22u3n =dcctkt	u13n	u14n =u2u7n =dcwrwt	u15n =u3u5n	u16n =u24n =dcccct
Треугольная грань
Икосаэдр Конвей Геодезический	nI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}1,1	unI Архивная копия от 30 декабря 2016 на Wayback Machine {3,5+}2,2	xnI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}3,3	u2nI Архивная копия от 30 декабря 2016 на Wayback Machine {3,5+}4,4	{3,5+}5,5	uxnI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}6,6	vrvnI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}7,7	u3nI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}8,8	x2nI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}9,9	{3,5+}10,10	{3,5+}11,11	u2xnI Архивная копия от 10 января 2017 на Wayback Machine {3,5+}12,12	{3,5+}13,13	dcwrwdnI Архивная копия от 9 января 2017 на Wayback Machine {3,5+}14,14	{3,5+}15,15	u4nI {3,5+}16,16
Двойственный оператор	z =dk	cz =cdk	yz =tkdk	c2z =ccdk	c5z	cyz =ctkdk	wwz =wrwdk	c3z =cccdk	y2z =tktkdk	cc5z	c11z	c2yz =c2tkdk	c13z	cwwz =cwrwdk	c3c5z	c4z =ccccdk
Додекаэдр Конвей Голдберг	zD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}1,1	czD Архивная копия от 7 апреля 2016 на Wayback Machine {5+,3}2,2	yzD Архивная копия от 30 декабря 2016 на Wayback Machine {5+,3}3,3	cczD Архивная копия от 7 апреля 2016 на Wayback Machine {5+,3}4,4	{5+,3}5,5	cyzD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}6,6	wrwzD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}7,7	c3zD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}8,8	y2zD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}9,9	{5+,3}10,10	G{5+,3}11,11	ccyzD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}12,12	{5+,3}13,13	cwrwzD Архивная копия от 9 января 2017 на Wayback Machine G{5+,3}14,14	{5+,3}15,15	cccczD Архивная копия от 9 января 2017 на Wayback Machine {5+,3}16,16

Класс III

Большинство геодезических многогранников и двойственные к многогранникам Голдберга G(n,m) нельзя построить с помощью операторов, производных от операторов Конвея. Операция whirl создаёт многогранник Голдберга G(2,1) с новыми шестиугольными гранями вокруг каждой исходной вершины, а n-whirl образует G(n,n-1). На формах с икосаэдральной симметрией t5g эквивалентен в этом случае whirl. Операция v (=volute = виток, оборот) представляет треугольное подразделение, двойственное whirl. На икосаэдральных формах операция может быть осуществлена с помощью производного оператора k5s, pentakis snub.

Две последовательные операции whirl создают G(3,5). В общем случае операция whirl может преобразовать G(a,b) в G(a+3b,2a-b) для a>b с тем же самым хиральным направлением. Если хиральное направление обратное, G(a,b) становится G(2a+3b,a-2b) для a>=2b, и G(3a+b,2b-a) для a<2b.

Класс III: Операции подразбиения на неравные части

Операция Составная	v2,1 =v	v3,1	v3,2=v3	v4,1 =vn	v4,2 =vu	v5,1	v4,3=v4	v5,2 =v3n	v6,1	v6,2 =v3,1u	v5,3 =vv	v7,1 =v3n	v5,4=v5	v6,3 =vx	v7,2
T	7	13	19	21 7×3	28 7×4	31	37	39 13×3	43	52 13×4	49 7×7	57 19×3	61	63 9×7	67
Треугольная грань
Икосаэдр Конвей Геодезический	vI {3,5+}2,1	v3,1I {3,5+}3,1	v3I {3,5+}3,2	vnI Архивная копия от 3 февраля 2017 на Wayback Machine {3,5+}4,1	vuI {3,5+}4,2	{3,5+}5,1	v4I {3,5+}4,3	v3nI {3,5+}5,2	{3,5+}6,1	v3,1uI {3,5+}6,2	vvI {3,5+}5,3	v3nI {3,5+}7,1	v5I {3,5+}5,4	vxI Архивная копия от 8 января 2018 на Wayback Machine {3,5+}6,3	v7,2I {3,5+}7,2
Оператор	w	w3,1	w3	wz	wc	w5,1	w4	w3,1z	w6,1	w3,1c	ww	w3z	w5	wy	w7,2
Додекаэдр Конвей	wD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}2,1	w3,1D {5+,3}3,1	w3D {5+,3}3,2	wzD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}4,1	wcD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}4,2	w5,1D {5+,3}5,1	w4D {5+,3}4,3	w3zD {5+,3}5,2	{5+,3}6,1	w3,1cD {5+,3}6,2	wwD Архивная копия от 21 октября 2016 на Wayback Machine {5+,3}5,3	w3zD {5+,3}7,1	w5D {5+,3}5,4	wyD Архивная копия от 8 января 2018 на Wayback Machine {5+,3}6,3	w7,2D {5+,3}7,2

Другие операции класса III: Операции подразбиения на неравные части

Операция Составная	v8,1	v6,4 =v3u	v7,3	v8,2 =wcz	v6,5=v6 =vrv3,1	v9,1 =vv3,1	v7,4	v8,3	v9,2	v7,5	v10,1 =v4n	v8,4 =vuu	v9,3 =v3,1x	v7,6=v7	v8,6 v4u
T	73	76 19×4	79	84 7×4×3	91 13×7		93	97	103	109	111 37×3	112 7×4×4	117 13×9	127	148 37×4
Треугольная грань
Икосаэдр Конвей Геодезический	v8,1I {3,5+}8,1	v3uI {3,5+}6,4	v7,3I {3,5+}7,3	vunI {3,5+}8,2	vv3,1I {3,5+}6,5	vrv3,1I {3,5+}9,1	v7,4I {3,5+}7,4	v8,3I {3,5+}8,3	v9,2I {3,5+}9,2	v7,5I {3,5+}7,5	v4nI {3,5+}10,1	vuuI {3,5+}8,4	v3,1xI {3,5+}9,3	v7I {3,5+}7,6	v4uI {3,5+}8,6
Оператор	w8,1	wrw3,1	w7,3	w3,1c	wcz	w3,1w	w7,4	w8,3	w9,2	w7,5	w4z	wcc	w3,1y	w7	w4c
Додекаэдр Конвей	w8,1D {5+,3}8,1	w3cD {5+,3}6,4	w7,3D {5+,3}7,3	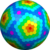wczD {5+,3}8,2	ww3,1D {5+,3}6,5	wrw3,1D {5+,3}9,1	w7,4D {5+,3}7,4	w8,3D {5+,3}8,3	w9,2D {5+,3}9,2	w7,5D {5+,3}7,5	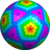w4zD {5+,3}10,1	wccD {5+,3}8,4	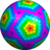w3,1yD {5+,3}9,3	w7D {5+,3}7,6	w4cD {5+,3}8,6

Примеры многогранников по симметрии

Повторение операций, начав с простой формы, может дать многогранники с большим числом граней, сохраняющих симметрию затравки.

Тетраэдральная симметрия

• 
  t6dtT
• 
  atT
• 
  tatT
• 
  stT
• 
  XT (10e)
• 
  dXT (10e)
• 
  m3T
• 
  b3T
• 
  dHccC
• 
  dFtO
• 
  FtO

Октаэдральная симметрия

• 
  daC Архивная копия от 4 января 2017 на Wayback Machine (2e)
• 
  cC (4e) * Архивная копия от 4 января 2017 на Wayback Machine
• 
  dcC (4e) * Архивная копия от 4 января 2017 на Wayback Machine
• 
  cO Архивная копия от 4 января 2017 на Wayback Machine (4e)
• 
  akC (6e) * Архивная копия от 4 января 2017 на Wayback Machine
• 
  dakC Архивная копия от 4 января 2017 на Wayback Machine (6e)
• 
  m3C (6e)
• 
  m3O (6e)
• 
  b3C (6e)
• 
  b3O (6e)
• 
  atC Архивная копия от 4 января 2017 на Wayback Machine (6e)
• 
  qC (6e)
• 
  edaC Архивная копия от 4 января 2017 на Wayback Machine (8e)
• 
  dktO=tkC Архивная копия от 4 января 2017 на Wayback Machine (9e)
• 
  taaC (12e) * Архивная копия от 4 января 2017 на Wayback Machine
• 
  XO (10e)
• 
  XC (10e)
• 
  dXO (10e)
• 
  dXC (10e)
• 
  cdkC Архивная копия от 4 января 2017 на Wayback Machine (12e)
• 
  ccC Архивная копия от 4 января 2017 на Wayback Machine (16e)
• 
  tkdkC Архивная копия от 4 января 2017 на Wayback Machine (18e)
• 
  tatO Архивная копия от 4 января 2017 на Wayback Machine (18e)
• 
  tatC Архивная копия от 4 января 2017 на Wayback Machine (18e)
• 
  l6l8taC Архивная копия от 4 марта 2017 на Wayback Machine (22e)
• 
  ccdkC Архивная копия от 4 января 2017 на Wayback Machine (48e)
• 
  wrwC Архивная копия от 16 января 2017 на Wayback Machine (49e)
• 
  cccC Архивная копия от 4 января 2017 на Wayback Machine (64e)
• 
  tktkC Архивная копия от 4 января 2017 на Wayback Machine (81e)
• 
  H1taC
• 
  H2taC
• 
  dH1taC
• 
  dH2taC

Хиральные

• 
  wC Архивная копия от 4 января 2017 на Wayback Machine (7e)
• 
  saC Архивная копия от 4 января 2017 на Wayback Machine (10e)
• 
  gaC Архивная копия от 4 января 2017 на Wayback Machine (10e)
• 
  saC Архивная копия от 4 января 2017 на Wayback Machine (10e)
• 
  stO Архивная копия от 4 января 2017 на Wayback Machine (15e)
• 
  stC Архивная копия от 4 января 2017 на Wayback Machine (15e)

Изоэдральная симметрия

• 
  kD Архивная копия от 3 марта 2017 на Wayback Machine = daD (2e)
• 
  kD (3e) * Архивная копия от 3 марта 2017 на Wayback Machine
• 
  dkD=tI (3e) * Архивная копия от 3 марта 2017 на Wayback Machine
• 
  cI (4e) * Архивная копия от 3 марта 2017 на Wayback Machine
• 
  t5daD = cD (4e) * Архивная копия от 3 марта 2017 на Wayback Machine
• 
  dcI (4e) * Архивная копия от 3 марта 2017 на Wayback Machine
• 
  dakD (6e) * Архивная копия от 3 марта 2017 на Wayback Machine
• 
  atD Архивная копия от 3 марта 2017 на Wayback Machine (6e)
• 
  atI = akD (6e) * Архивная копия от 3 марта 2017 на Wayback Machine
• 
  qD Архивная копия от 3 марта 2017 на Wayback Machine (6e)
• 
  m3D (6e)
• 
  m3I (6e)
• 
  b3D (6e)
• 
  b3I (6e)
• 
  edaD (8e) * Архивная копия от 3 марта 2017 на Wayback Machine
• 
  tkdD (9e) * Архивная копия от 3 марта 2017 на Wayback Machine
• 
  gaD (10e) * Архивная копия от 3 марта 2017 на Wayback Machine
• 
  XI (10e)
• 
  XD (10e)
• 
  dXI (10e)
• 
  dXD (10e)
• 
  teD (12e) * Архивная копия от 3 марта 2017 на Wayback Machine
• 
  cdkD Архивная копия от 3 марта 2017 на Wayback Machine (12e)
• 
  m3aI (12e)
• 
  tatI Архивная копия от 3 марта 2017 на Wayback Machine = takD (18e)
• 
  tatD Архивная копия от 3 марта 2017 на Wayback Machine (18e)
• 
  atkD Архивная копия от 3 марта 2017 на Wayback Machine (18e)
• 
  m3tD (18e)
• 
  qtI Архивная копия от 4 марта 2017 на Wayback Machine = t5t6otI (18e)
• 
  dqtI Архивная копия от 4 марта 2017 на Wayback Machine = k5k6etI (18e)
• 
  actI Архивная копия от 3 марта 2017 на Wayback Machine (24e)
• 
  kdktI Архивная копия от 3 марта 2017 на Wayback Machine (27e)
• 
  tktI Архивная копия от 3 марта 2017 на Wayback Machine (27e)
• 
  dctkD Архивная копия от 3 марта 2017 на Wayback Machine (36e)
• 
  ctkD Архивная копия от 3 марта 2017 на Wayback Machine (36e)
• 
  k6k5tI Архивная копия от 3 марта 2017 на Wayback Machine
• 
  kt5daD Архивная копия от 3 марта 2017 на Wayback Machine
• 
  dHtmD
• 
  F1taD
• 
  F2taD
• 
  dF1taD
• 
  dF2taD

Хиральные

• 
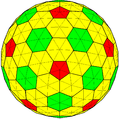
  dsD (5e)
• 
  sD (5e)
• 
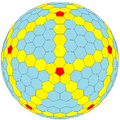
  wD (7e)
• 
  k5sD (7e)
• 
  saD (10e)
• 
  saD (10e)
• 
  g3D (11e)
• 
  s3D (11e)
• 
  g3I (11e)
• 
  s3I (11e)
• 
  stI (15e)
• 
  stD (15e)
• 
  wtI (21e)
• 
  k5k6stI (21e)

Диэдральная симметрия

• 
  t4daA4=cA4
• 
  t4daA4=cA4 (side)
• 
  t4daA4=cA4 (top)
• 
  tA4
• 
  tA5
• 
  htA2
• 
  htA3=I
• 
  htA4
• 
  htA5
• 
  eP3 = aaP3
• 
  eA4 = aaA4

Тороидальная симметрия

Тороидальные мозаики существуют на плоском торе, на поверхности дуоцилиндра в четырёхмерном пространстве, но могут быть спроектированы в трёхмерное пространство как обычный тор. Эти мозаики топологически подобны подмножествам мозаик евклидовой плоскости.

• 
  1x1 правильный квадратный тор, {4,4}_1,0
• 
  Правильный 4x4 квадратный тор, {4,4}_4,0
• 
  tQ24×12 проекция на тор
• 
  taQ24×12 проекция на тор
• 
  actQ24×8 проекция на тор
• 
  tH24×12 проекция на тор
• 
  taH24×8 проекция на тор
• 
  kH24×12 проекция на тор

Евклидова квадратная симметрия

• 
  tQ
• 
  cQ
• 
  akQ
• 
  HdXQ
• 
  dHdXQ

Евклидова треугольная симметрия

• 
  tH
• 
  cΔ
• 
  cH
• 
  ctH
• 
  dakH
• 
  aaaH
• 
  aaaH, равносторонняя

См. также

• Однородные многогранники
• Алгоритмы компьютерной графики:
  • Подразделение поверхности Ду — Сабина – expand operator
  • Алгоритм подразделения поверхности Катмулла — Кларка – оператор ortho
• Многогранник Годберга
• Симметрогранник

Ссылки

• George Hart's Conway interpreter Архивная копия от 29 ноября 2014 на Wayback Machine: generates polyhedra in VRML, taking Conway notation as input. Also includes helpful explanations of the operations.
  • Polyhedra Names Архивная копия от 12 ноября 2020 на Wayback Machine
• Vertex- and edge-truncation of the Platonic and архимедовых тел leading to vertex-transitive polyhedra Архивная копия от 16 марта 2019 на Wayback Machine Livio Zefiro
• polyHédronisme Архивная копия от 25 апреля 2012 на Wayback Machine: generates polyhedra in HTML5 canvas, taking Conway notation as input
• Weisstein, Eric W. Conway Polyhedron Notation (англ.) на сайте Wolfram MathWorld.
• John Conway's notation Архивная копия от 3 февраля 2018 на Wayback Machine Visualization of Conway Polyhedron Notation Архивная копия от 9 апреля 2017 на Wayback Machine
• Weisstein, Eric W. Truncation (англ.) на сайте Wolfram MathWorld. (truncate)
• Weisstein, Eric W. Rectification (англ.) на сайте Wolfram MathWorld. (ambo)
• Weisstein, Eric W. Cumulation or Apiculation (англ.) на сайте Wolfram MathWorld. (kis)
• Conway operators, PolyGloss, Wendy Krieger Архивная копия от 22 октября 2017 на Wayback Machine
• Derived Solids