Полином Жегалкина
Полином Жегалкина — многочлен над полем , то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения — исключающее или. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой (АНФ).
Теорема Жегалкина — утверждение о существовании и единственности представления всякой булевой функции в виде полинома Жегалкина[1].
Полином Жегалкина представляет собой сумму по модулю два попарно различных произведений неинвертированных переменных, где ни в одном произведении ни одна переменная не встречается больше одного раза, а также (если необходимо) константы 1[1]. Формально полином Жегалкина можно представить в виде
или в более формализованном виде как
Примеры полиномов Жегалкина:
Предпосылки[править | править код]
По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали:
- Хотя бы одна функция, не сохраняющая 0.
- Хотя бы одна функция, не сохраняющая 1.
- Хотя бы одна нелинейная функция.
- Хотя бы одна немонотонная функция.
- Хотя бы одна несамодвойственная функция.
Этому требованию отвечает, в частности, система функций (конъюнкция, сложение по модулю два, константа 1). На её основе и строятся полиномы Жегалкина.
Существование и единственность представления[править | править код]
По теореме Жегалкина каждая булева функция единственным образом представляется в виде полинома Жегалкина. Теорема доказывается следующим образом. Заметим, что различных булевых функций от n переменных штук. При этом конъюнкций от n переменных существует ровно 2n, так как из n возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит 0 или 1, то есть существует различных полиномов Жегалкина от n переменных. Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него (любой один, если таких несколько). Подставив единицы на места этих переменных и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом.
Представление функции в виде полинома Жегалкина[править | править код]
С помощью эквивалентных преобразований ДНФ[править | править код]
По сравнению с ДНФ в полиноме Жегалкина отсутствуют операции ИЛИ и НЕ. Таким образом, полином Жегалкина можно получить из ДНФ, выразив операции ИЛИ и НЕ через операции сложение по модулю два, и константу 1. Для этого применяются следующие соотношения:
Ниже приведён пример преобразования ДНФ в полином Жегалкина:
При преобразованиях использованы соотношения
С помощью эквивалентных преобразований СДНФ[править | править код]
СДНФ обладает тем свойством, что при любых значениях входных переменных в единицу обращается не более одного члена выражения. Для таких выражений операция дизъюнкции эквивалентна операции сложение по модулю два.
При преобразовании СДНФ в полином Жегалкина достаточно заменить все дизъюнкции на операции сложение по модулю два и избавиться от инверсий при помощи эквивалентного преобразования
С помощью карты Карно[править | править код]

Логическая функция трёх переменных , представленная в виде карты Карно, преобразуется в полином Жегалкина следующими шагами:
- Рассматриваем все ячейки карты Карно в порядке возрастания количества единиц в их кодах. Для функции трёх переменных последовательность ячеек будет 000—100 — 010—001 — 110—101 — 011—111. Каждой ячейке карты Карно сопоставляем член полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке 111 соответствует член ABC, ячейке 101 — член AC, ячейке 010 — член B, ячейке 000 — член 1.
- Если в рассматриваемой ячейке находится 0, переходим к следующей ячейке.
- Если в рассматриваемой ячейке находится 1, добавляем в полином Жегалкина соответствующий член, инвертируем в карте Карно все ячейки, где этот член равен 1, и переходим к следующей ячейке. Например, если при рассмотрении ячейки 110 в ней оказывается единица, то в полином Жегалкина добавляется член AB и инвертируются все ячейки карты Карно, где A = 1 и B = 1. Если единице равна ячейка 000, то в полином Жегалкина добавляется член 1 и инвертируется вся карта Карно.
- Процесс преобразования можно считать законченным, когда после очередной инверсии все ячейки карты Карно становятся нулевыми.
Метод треугольника[править | править код]

Метод треугольника (часто называемый методом треугольника Паскаля) позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:
- Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от 000…00 до 111…11.
- Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности.
- Ячейка в каждом последующем столбце получается путём суммирования по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже.
- Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности.
- Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке 111 соответствует член ABC, ячейке 101 — член AC, ячейке 010 — член B, ячейке 000 — член 1 и т. д.
- Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина.
Метод треугольника основан на теореме, предложенной В. П. Супруном, не связанной напрямую с треугольником Паскаля. В 1985 году метод двоичного треугольника было предложено использовать для преобразования вектора значений совершенной дизъюнктивной нормальной формы в вектор коэффициентов полинома Жегалкина для произвольной симметрической булевой функции. В 1987 году метод был расширен для произвольной булевой функции. Отметим, что метод треугольника позволяет строить полином Рида — Маллера с отрицательной поляризацией как для симметрических функций, так и для произвольных[источник не указан 2205 дней].
Метод БПФ[править | править код]
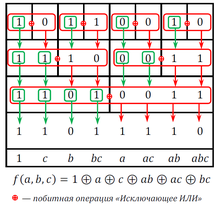
Наиболее экономным с точки зрения объёма вычислений и целесообразным для построения полинома Жегалкина вручную является метод быстрого преобразования Фурье (БПФ).
Строим таблицу, состоящую из 2N столбцов и N + 1 строк, где N — количество переменных в функции. В верхней строке таблицы размещаем вектор значений функции, то есть последний столбец таблицы истинности.
Каждую строку полученной таблицы разбиваем на блоки (чёрные линии на рисунке). В первой строке блок занимает одну клетку, во второй строке — две, в третьей — четыре, в четвёртой — восемь и т. д. Каждому блоку в некоторой строке, который мы будем называть «нижний блок», всегда соответствует ровно два блока в предыдущей строке. Будем называть их «левый верхний блок» и «правый верхний блок».
Построение начинается со второй строки. Содержимое левых верхних блоков без изменения переносится в соответствующие клетки нижнего блока (зелёные стрелки на рисунке). Затем над правым верхним и левым верхним блоками побитно производится операция «сложение по модулю два», и полученный результат переносится в соответствующие клетки правой части нижнего блока (красные стрелки на рисунке). Эта операция проводится со всеми строками сверху вниз и со всеми блоками в каждой строке. После окончания построения в нижней строке оказывается строка чисел, которая является коэффициентами полинома Жегалкина, записанными в той же последовательности, что и в описанном выше методе треугольника.
Метод суммирования[править | править код]
В разделе не хватает ссылок на источники (см. рекомендации по поиску). |

По таблице истинности легко вычислить отдельные коэффициенты полинома Жегалкина. Для этого нужно просуммировать по модулю 2 значения функции в тех строках таблицы, где переменные, отсутствующие в конъюнкции, принимают нулевые значения.
Предположим для примера, что нужно найти коэффициент при конъюнкции xz для функции трёх переменных f(x, y, z). В этой конъюнкции отсутствует переменная y. Найдём входные наборы, в которых переменная y принимает нулевое значение. Это наборы 0, 1, 4, 5 (000, 001, 100, 101). Тогда коэффициент при конъюнкции xz равен
Поскольку в свободном члене отсутствуют все переменные, то
Для члена, куда входят все переменные, в сумму входят все значения функции:
Представим графически коэффициенты полинома Жегалкина как суммы по модулю 2 значений функций в некоторых точках. Для этого построим квадратную таблицу, где каждый столбец представляет собой значение функции в одной из точек, а строка — коэффициент полинома Жегалкина. Точка на пересечении некоторого столбца и строки означает, что значение функции в данной точке входит в сумму для данного коэффициента полинома (см. рисунок). Назовём эту таблицу TN, где N — число переменных функции.
Существует закономерность, которая позволяет получить таблицу для функции N переменных, имея таблицу для функции N − 1 переменных. Новая таблица TN+1 компонуется как матрица 2 × 2 таблиц TN, причём правый верхний блок матрицы очищается.
См. также[править | править код]
Примечания[править | править код]
- ↑ 1 2 Капитонова Ю. В., Кривой С. Л., Летичевский А. А. Лекции по дискретной математике. — СПб., БХВ-Петербург, 2004. — ISBN 5-94157-546-7, с. 110—111.
- ↑ В. П. Супрун. Табличный метод полиномиального разложения булевых функций // Кибернетика. — 1987. — № 1. — С. 116—117.
- ↑ В. П. Супрун. Основы теории булевых функций. — М.: Ленанд / URSS. — 2017. — 208 с.
Литература[править | править код]
- Яблонский С. В. Введение в дискретную математику. — М.: Наука. — 1986
- Марченков С. С. Замкнутые классы булевых функций. — М.: Физматлит. — 2000
- Супрун В. П. Основы теории булевых функций. — М.: Ленанд / URSS. — 2017.
Для улучшения этой статьи по математике желательно: |


















