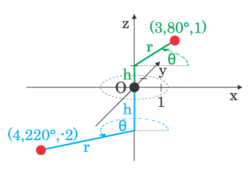
Цилиндрическая система координат
Материал из Википедии — свободной энциклопедии
Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой z), которая задаёт высоту точки над плоскостью.
Точка P даётся как 
. В терминах прямоугольной системы координат:
— расстояние от O до P', ортогональной проекции точки P на плоскость XY. Или то же самое, что расстояние от P до оси Z.
— угол между осью X и отрезком OP'.- z равна аппликате точки P.
При использовании в физических науках и технике международный стандарт ISO 31-11 рекомендует использовать обозначения .
Некоторые математики используют 
.
Цилиндрические координаты удобны при анализе поверхностей, симметричных относительно какой-либо оси, если ось Z взять в качестве оси симметрии. Например, бесконечно длинный круглый цилиндр в прямоугольных координатах имеет уравнение x2 + y2 = c2, а в цилиндрических — очень простое уравнение ρ = c. Отсюда и идёт для данной системы координат имя «цилиндрическая».
[править] Переход к другим системам координат
Поскольку цилиндрическая система координат — только одна из многих трёхмерных систем координат, существуют законы преобразования координат между цилиндрической системой координат и другими системами.
[править] Декартова система координат
Закон преобразования координат от цилиндрических к декартовым:
Закон преобразования координат от декартовых к цилиндрическим:
Якобиан равен:
- J = ρ.
[править] Дифференциальные характеристики
Цилиндрические координаты являются ортогональными, поэтому метрический тензор имеет в них диагональный вид:
- Квадрат дифференциала длины кривой
- Коэффициенты Ламэ имеют вид:
:
Остальные равны нулю.
 |
В этой статье не хватает ссылок на источники информации.
Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена.
Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. |
