Фильтр (электроника)

Фильтр в электронике — устройство для выделения желательных компонентов спектра электрического сигнала и/или подавления нежелательных.

Типы фильтров

Фильтры, находящие применение в обработке сигналов, бывают

• аналоговыми и цифровыми
• пассивными или активными
• линейными и нелинейными
• рекурсивными и нерекурсивными

Среди множества рекурсивных фильтров отдельно выделяют следующие фильтры (по виду передаточной функции):

• фильтры Чебышёва
• фильтры Бесселя
• фильтры Баттерворта
• эллиптические фильтры

По степени многочлена в знаменателе передаточной функции (см. также ЛАФЧХ) различают фильтры первого, второго и более высоких порядков. Крутизна ЛАЧХ фильтра 1-го порядка в полосе подавления равна 20 дБ на декаду, фильтра 2-го порядка — 40 дБ на декаду, и т. д.

По тому, какие частоты фильтром пропускаются (задерживаются), фильтры подразделяются на

• фильтры нижних частот (ФНЧ)
• фильтры верхних частот (ФВЧ)
• полосно-пропускающие фильтры (ППФ)
• полосно-задерживающие (режекторные) фильтры (ПЗФ)
• фазовые фильтры

Принцип работы пассивных аналоговых фильтров

В конструкциях пассивных аналоговых фильтров используют сосредоточенные или распределённые реактивные элементы, такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя их, можно добиться усиления или ослабления гармоник составляющих спектра (они могут не являться гармониками) с нужными частотами. Другой принцип построения пассивных аналоговых фильтров — это использование механических (акустических) колебаний в механическом резонаторе той или иной конструкции.

Фильтры на сосредоточенных элементах

В качестве простейших фильтров низких и высоких частот могут использоваться RC-цепь или LR-цепь. Однако они имеют невысокую крутизну АЧХ в полосе подавления, недостаточную во многих случаях: всего 6 дБ на октаву (или 20 дБ на декаду) — для RC-фильтра, являющегося фильтром 1-го порядка и 40 дБ/декада для LC-фильтра, являющегося фильтром 2-го порядка. В пассивных фильтрах добавление в схему фильтра любого реактивного компонента увеличивает порядок фильтра на 1.

RС-фильтр нижних частот 1-го порядка

Пассивный RС-фильтр нижних частот 1-го порядка

Простейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора $R$ и конденсатора $C$, образующего делитель напряжения входного сигнала. Комплексный коэффициент передачи $K_{RC}$ такого делителя:

$K_{RC}={\frac {U_{a}}{U_{e}}}={\frac {Z_{C}}{R+Z_{C}}}={\frac {1/j\omega C}{R+1/j\omega C}}={\frac {1}{T^{2}\omega ^{2}+1}}-j\cdot {\frac {T\omega }{T^{2}\omega ^{2}+1}},$

где $T=RC$ — постоянная времени RС-цепи.

Модуль коэффициента передачи этой цепи:

$|K_{RC}|={\sqrt {\frac {1}{\omega ^{2}/\omega _{0}^{2}+1}}},$

где $\omega _{0}=1/T.$

При входной частоте $\omega \ll \omega _{0}$ модуль коэффициента передачи близок к 1, при $\omega \gg \omega _{0}$ модуль коэффициента передачи близок к 0, на частоте $\omega =\omega _{0}$ модуль коэффициента передачи равен $|K_{RC}|=1/{\sqrt {2}}$ — уменьшение относительно единичного коэффициента передачи приблизительно на 3,01 дБ, эта частота называется частотой среза фильтра. В полосе подавления при частоте много выше частоты среза модуль коэффициента передачи уменьшается на 20 дБ на декаду изменения частоты.

LС-фильтр нижних частот 2-го порядка

Простейший пассивный LC-фильтр нижних частот 2-го порядка

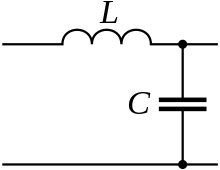
На рисунке показан пример простейшего LC-фильтра нижних частот 2-го порядка: при подаче гармонического сигнала определённой частоты на вход фильтра (на рисунке слева) напряжение на выходе фильтра (справа) в установившемся режиме определяется отношением реактивных сопротивлений катушки индуктивности ($X_{L}=\omega L$) и конденсатора ($X_{C}=1/\omega C$).

Коэффициент передачи ФНЧ можно вычислить, рассматривая этот фильтр как делитель напряжения, образованный реактивными сопротивлениями.

Комплексное (с учетом сдвига фаз между напряжением и током) сопротивление катушки индуктивности есть $Z_{L}=j\omega L=jX_{L}$ и комплексное сопротивление конденсатора $Z_{C}=1/(j\omega C)=-jX_{C}$, где ${j}^{2}=-1$ — мнимая единица, $\omega$ — угловая частота входного гармонического сигнала, поэтому для ненагруженного LC-фильтра коэффициент передачи $K$ будет выражаться формулой для делителя напряжения:

$K={\frac {Z_{C}}{Z_{L}+Z_{C}}}$.

Подставляя в формулу выражения для комплексных сопротивлений, получим для частотно-зависимого коэффициента передачи:

$K(\omega )={\frac {1}{1-\omega ^{2}\,LC}}={\frac {1}{1-(\omega /\omega _{0})^{2}}}$.

Как видно, коэффициент передачи ненагруженного идеального ФНЧ источником сигнала для которого является идеальный генератор напряжения с нулевым внутренним сопротивлением неограниченно растет с приближением к резонансной частоте $\omega _{0}=1/{\sqrt {LC}}$, так как знаменатель выражения стремится к нулю. При повышении частоты выше резонансной — убывает. На очень низких частотах коэффициент передачи ФНЧ близок к единице, на очень высоких — к нулю.

Принято называть зависимость модуля комплексного коэффициента передачи фильтра от частоты амлитудно-частотной характеристикой (АЧХ), а зависимость фазы от частоты — фазо-частотной характеристикой (ФЧХ).

В реальных схемах к выходу фильтра подключается активная нагрузка, которая понижает добротность фильтра и устраняет острый всплеск коэффициента передачи вблизи частоты резонанса $\omega _{0}$.

Величину $\rho ={\sqrt {L/C}}$ называют характеристическим сопротивлением фильтра или волновым сопротивлением фильтра. Если ФНЧ нагрузить на активное сопротивление, равное характеристическому, то передаточная функция станет нерезонансной, коэффициент передачи будет примерно постоянный для частот $\omega <\omega _{0}$, и убывающий как $1/\omega ^{2}$ на частотах выше $\omega _{0}$. На частоте $\omega _{0}$ коэффициент передачи такого ФНЧ уменьшается на 3 дБ относительно значения коэффициента передачи на низкой частоте, эту частоту называют частотой среза фильтра. На частотах много выше частоты среза коэффициент передачи уменьшается на 40 дБ на декаду изменения частоты.

Аналогичным образом строится и LC-фильтр верхних частот. В схеме ФВЧ меняются местами катушка индуктивности и конденсатор. Для ненагруженного ФВЧ получается выражение для коэффициента передачи:

$K(\omega )={\frac {(\omega /\omega _{0})^{2}}{1-(\omega /\omega _{0})^{2}}}$.

На очень низких частотах модуль коэффициента передачи ФВЧ близок к нулю. На очень высоких — к единице.

См. также: Резонанс напряжений

Фильтры с распределёнными параметрами (фильтры СВЧ)

На сверхвысоких частотах сосредоточенные элементы (конденсаторы и катушки индуктивности) практически не используются, так как с ростом частоты их типичные для этого диапазона номиналы, а следовательно и габариты, уменьшаются настолько, что изготовление их становится невозможным. Поэтому применяются так называемые линии с распределёнными параметрами, в которых индуктивность, ёмкость и активная нагрузка равномерно или неравномерно распределены по всей линии. Так, элементарный ФНЧ, рассматриваемый в предыдущем разделе, состоит из двух сосредоточенных элементов, представляющих собой резонатор; в случае же распределённых параметров фильтр будет состоять из одного элемента-резонатора (например отрезка микрополосковой линии или металлического стержня).

Конструкции СВЧ фильтров весьма разнообразны, и выбор конкретной реализации зависит от предъявляемых к устройству требований (значение рабочих частот, добротность, максимальное затухание в полосе задержания, расположение паразитных полос пропускания).

Проектирование фильтров на распределённых параметрах является достаточно сложным процессом, состоящим из двух этапов: получение электрических параметров, исходя из требований к устройству; получение габаритных параметров из полученных электрических. В основе современных методов проектирования микроволновых фильтров лежит теория связанных резонаторов.

Электромеханические фильтры

Основная статья: Электромеханический фильтр

ЭМФ с дисковыми изгибными резонаторами и магнитрострикционными преобразователями

Электромеханический фильтр (ЭМФ) содержит механическую резонансную систему (резонатор) той или иной конструкции. На входе и на выходе фильтра стоят электромеханические преобразователи, которые преобразуют электрические колебания сигнала в механические колебания рабочего тела фильтра и обратно.

ЭМФ получили распространение в трактах промежуточной частоты высококачественных радиосистем (в том числе военных, морских, радиолюбительских и других). Их преимуществом является значительно бо́льшая, чем у эквивалентных LC-фильтров, добротность, позволяющая достичь высокой избирательности, необходимой для разделения близких по частоте радиосигналов в приёмниках.

Фильтры на поверхностных акустических волнах (ПАВ)

Типичное ПАВ устройство, в основе которого применяется встречно-гребенчатый преобразователь, используемое в качестве полосового фильтра.

Принцип работы активных аналоговых фильтров

Активные аналоговые фильтры строятся на основе усилителей, охваченных петлёй обратной связи (положительной или отрицательной). В активных фильтрах возможно избежать применения катушек индуктивности, что позволяет уменьшить физические размеры устройств, упростить и удешевить их изготовление.

Применение

LC-фильтры используются в силовых электрических цепях для гашения помех и для сглаживания пульсаций напряжения после выпрямителя. В каскадах радиоэлектронной аппаратуры часто применяются перестраиваемые LC-фильтры, например, простейший LC-контур, включенный на входе средневолнового радиоприёмника обеспечивает настройку на определённую радиостанцию.

Фильтры используются в звуковой аппаратуре в многополосных эквалайзерах для корректировки АЧХ, для разделения сигналов низких, средних и высоких звуковых частот в многополосных акустических системах, в схемах частотной коррекции магнитофонов и др.

См. также

• ADSL-фильтр
• Спектр (электричество)
• Sinc-фильтр
• Корреляционный фильтр
• Согласованный фильтр
• Сглаживающий фильтр

Литература

• Р. Богнер, А. Константинидис. Введение в цифровую фильтрацию. — Москва: Мир, 1976.
• Э. Оппенгейм. Применение цифровой обработки сигналов. — Москва: Мир, 1980.
• Ханзел Г.Е. Справочник по расчёту фильтров. Под ред. А. Е. Знаменского. 288 с. с ил.. — Москва: Советское радио, 1974.

Ссылки

• Онлайн расчёт RC фильтров (ФНЧ и ФВЧ)
• Фильтры средних и верхних частот
• Схемы фильтров
• Про сетевые фильтры, скачки, заземление и многое другое