Metaball

1: Взаимодействие двух положительных метасфер.
2: Взаимодействие положительной и отрицательной метасферы создает вмятину на положительной метасфере.

Metaball (рус. Метасфера, также встречается «метаболл») — n-мерный объект в компьютерной графике, представляющий собою замкнутую сглаженную поверхность. Техника рендеринга метасфер была изобретена Джимом Блинном (англ. Jimm Blinn) в начале 1980-х годов.

Идея

Использование полигонов в компьютерной графике часто дает несглаженные модели, причем степень сглаженности сильно зависит от масштаба. Для получения гладких поверхностей используются различные методы, такие как B-сплайны и поверхности Безье. При использовании метасфер подразумевается, что в пространстве задано множество управляющих точек или частиц, обладающих потенциалом, и заданы функции зависимости потенциала от расстояния. Вычисляя потенциал поля, можно построить сглаженные изоповерхности довольно сложной формы.

Способ задания

Каждая управляющая точка определяет собственную n-мерную потенциальную функцию $U_{i}(x,y,z)$ (обычно n=3). Затем выбирается некое значение $U_{0}$ (потенциал), которое определяет форму метасферы (фактически, определяется эквипотенциальная поверхность). Таким образом, неравенство $\sum _{i=1}^{k}{\mbox{U}}_{i}(x,y,z)\leq {\mbox{U}}_{0}$ определяет, находится ли точка $(x,y,z)$ внутри поверхности, заданной $k$ управляющими точками, или нет.

Часто в качестве функции, задающей метасферу, используют $U(x,y,z)={\frac {1}{(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}}}$, где $(x_{0},y_{0},z_{0})$ — центр метасферы. Однако использование деления делает эту функцию неэффективной по скорости, поэтому обычно её заменяют аппроксимирующими полиномиальными функциями.

При поиске более эффективной функции потенциала желательно, чтобы она удовлетворяла следующим требованиям:

• Компактность носителя. Такая функция обращается в ноль за пределами некой ограничивающей сферы. При вычислении поля, создаваемого управляющей точкой, нет необходимости вычислять его, когда расстояние превышает радиус ограничивающей сферы. Иерархическая система отсечений может, таким образом, сильно сократить количество управляющих точек, необходимых для расчета поля в данной точке.
• Гладкость. Поскольку метасфера является результатом суперпозиции полей управляющих точек, её гладкость зависит от гладкости функции потенциала.

Простейшая функция потенциала, удовлетворяющая этим критериям: $U(r)=(1-r^{2})^{2}$, где $r$ — расстояние между управляющей точкой и заданной точкой пространства. Она также довольно эффективна, поскольку не использует деления и извлечения корня.

Более сложные модели используют для лучшего сглаживания гауссов потенциал, ограниченный конечным радиусом набора многочленов. Модель мягких объектов братьев Вивилл (англ. Wyvill) обеспечивает более высокую степень сглаженности и не использует квадратные корни.

Простое обобщение модели можно получить, заменяя расстояние между точками в функции потенциала расстоянием до прямой или расстоянием до поверхности.

Есть множество способов рендеринга метасфер. Для трехмерных метасфер чаще всего применяют рэйкастинг и алгоритм marching cubes.

Двухмерные метасферы были очень популярны в демо в 1990-х. Этот эффект также доступен в модуле XScreensaver.

Взаимодействие двух положительных метасфер, смоделированное в Bryce.
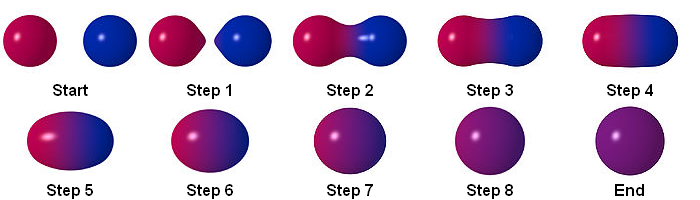
Обратите внимание, как две маленькие метасферы сливаются в одну большую.

Литература

• Blinn, James F.  «A Generalization of Algebraic Surface Drawing.» ACM Transactions on Graphics 1(3), July 1982, pp. 235—256.

См. также

• Система частиц
• Marching cubes

Ссылки

• Неявные поверхности — статья Поля Бурке (англ.)
• Метаобъекты на Blender-вики (англ.)
• Метасферы на сайте SIGGRAPH (англ.)
• Исследование метасфер и изоповерхностей на плоскости (статья на GameDev.net) (англ.)
• Использование двумерных метасфер в Photoshop (англ.)
• Введение в метасферы (англ.)