Гомотопические группы

Гомотопи́ческие гру́ппы — инвариант топологических пространств, одно из основных понятий алгебраической топологии.

Неформально говоря, они классифицируют отображения из многомерных сфер в заданное топологическое пространство с точностью до непрерывной деформации. Несмотря на простоту определения, гомотопические группы очень сложны в вычислении, даже для сфер. Это отличает их от групп гомологий, которые проще считаются, но сложнее определяются. Простейшим частным случаем гомотопических групп является фундаментальная группа.

Определение

Пусть $X$ — топологическое пространство, $x_{0}\in X$; $I^{n}\subset \mathbb {R} ^{n}$ — единичный куб, то есть $I^{n}=\{(t_{1},t_{2},\ldots ,t_{n}):0\leqslant t_{i}\leqslant 1\}$, и $\partial I^{n}$ — граница этого куба, то есть множество точек куба, такое, что $t_{i}=0$ или 1 для некоторого $i$. Множество гомотопических классов $[f]$ непрерывных отображений $f\colon I^{n}\to X$, для которых $f(\partial I^{n})=x_{0}\in X$ обозначается $\pi _{n}(X,x_{0})$ (причём $\partial I^{n}$ переходит в точку $x_{0}$ при всех отображениях и гомотопиях). На этом множестве можно определить умножение элементов следующим образом:

$[f][g]=[f*g]$,

где

$f*g(t_{1},t_{2},\ldots t_{n})=f(2t_{1},t_{2},\ldots t_{n})$, если $0\leqslant t_{1}\leqslant {\frac {1}{2}}$

$f*g(t_{1},t_{2},\ldots t_{n})=g(2t_{1}-1,t_{2},\ldots t_{n})$, если ${\frac {1}{2}}\leqslant t_{1}\leqslant 1$

Так как на границе куба $f=g=x_{0}$, то умножение определено корректно. Легко проверить, что $[f*g]$ зависит только от гомотопического класса $[f]$ и $[g]$. Это умножение удовлетворяет всем аксиомам группы. В случае $n=1$ получается композиция замкнутых путей и, следовательно, $\pi _{1}(X,x_{0})$ является фундаментальной группой. При n>1 $\pi _{n}(X,x_{0})$ называются высшими гомотопическими группами.

Непрерывному отображению пространств $F\colon (X,x_{0})\to (Y,y_{0})$ соответствует гомоморфизм $F_{*}\colon \pi _{n}(X,x_{0})\to \pi _{n}(Y,y_{0})$, причём это соответствие функториально, то есть произведению непрерывных отображений соответствует произведение гомоморфизмов гомотопических групп $(FG)_{*}=F_{*}G_{*}$, а тождественному отображению соответствует тождественный гомоморфизм $(id)_{*}=id_{*}$. Если отображение $F$ гомотопно $G$, то $F_{*}=G_{*}$.

Зависимость от начальной точки

В отличие от гомологических групп $H_{n}(X)$, в определение гомотопических групп $\pi _{n}(X,x_{0})$ входит выделенная точка $x_{0}$. На самом деле в случае линейно связных пространств гомотопические группы не зависят от выбора точки, хотя в общем случае канонического изоморфизма не существует.

Абелевость высших гомотопических групп

В то время как фундаментальная группа $\pi _{1}(X,x_{0})$ в общем случае неабелева, для всех n>1 $\pi _{n}(X,x_{0})$ абелевы, то есть $[f][g]=[g][f]$. Наглядное доказательство этого факта можно видеть на следующем рисунке (светло-синие области отображаются в точку $x_{0}$):

Абелевость высших гомотопических групп

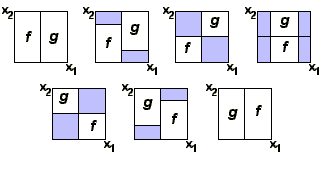
Относительные гомотопические группы и точная гомотопическая последовательность

Относительные гомотопические группы определяются для пространства $X$, его подпространства $A\subset X$ и выделенной точки $x_{0}\in X$. Пусть $I^{n}\subset \mathbb {R} ^{n}$ — единичный куб ($I^{n}=\{(t_{1},t_{2},\ldots t_{n}):0\leqslant t_{i}\leqslant 1\}$), $\partial I^{n}$ — граница этого куба, a $I^{n-1}\subset \partial I^{n}$ — грань куба, определяемая уравнением $t_{n}=0$. Множество гомотопических классов $[f]$ непрерывных отображений $f\colon I^{n}\to X$, для которых $f\colon I^{n-1}\to A$ и на остальных гранях $f\colon \partial I^{n}\setminus \operatorname {Int} (I^{n-1})\to x_{0}$ обозначается $\pi _{n}(X,A,x_{0})$ (причём $I^{n-1}$ переходит в $A$, а $\partial I^{n}\setminus \operatorname {Int} (I^{n-1})$ в точку $x_{0}$ при всех отображениях и гомотопиях).

Точно так же, как и раньше, можно доказать, что при $n\geqslant 2$ это множество образует группу — относительную гомотопическую группу порядка $n$. Если $n\geqslant 3$, то предыдущий рисунок доказывает, что $\pi _{n}(X,A,x_{0})$ — абелева. (При n=2 доказательство не проходит, так как точки $I^{1}=\{x:x_{2}=0\}$ могут переходить в точки $A$, отличные от $x_{0}$.)

Вложение $i\colon (A,x_{0})\to (X,x_{0})$ индуцирует гомоморфизм $i_{*}\colon \pi _{n}(A,x_{0})\to \pi _{n}(X,x_{0})$, а вложение $j\colon (X,x_{0})\to (X,A,x_{0})$ (здесь $(X,x_{0})$ следует понимать как $(X,x_{0},x_{0})$), индуцирует гомоморфизм $j_{*}\colon \pi _{n}(X,x_{0})\to \pi _{n}(X,A,x_{0})$. Любой элемент $[f]\in \pi _{n}(X,A,x_{0})$ определяется отображением $f$, которое, в частности, переводит $I^{n-1}$ в $A$, причём на $\partial I^{n-1}$ f тождественно равно $x_{0}$, определяя элемент из $\pi _{n-1}(A,x_{0})$. Таким образом мы получаем отображение $\partial \pi _{n}(X,A,x_{0})\to \pi _{n-1}(A,x_{0})$, которое является гомоморфизмом. Мы имеем следующую последовательность групп и гомоморфизмов:

$\dots ~{\longrightarrow }\pi _{n}(A,x_{0}){\stackrel {i_{*n}}{\longrightarrow }}\pi _{n}(X,x_{0}){\stackrel {j_{*n}}{\longrightarrow }}\pi _{n}(X,A,x_{0}){\stackrel {\partial _{n}}{\longrightarrow }}\pi _{n-1}(A,x_{0}){\longrightarrow }~\dots$

Эта последовательность является точной, то есть образ любого гомоморфизма совпадает с ядром следующего гомоморфизма. Отсюда в случае, когда $\pi _{n}(X,x_{0})=0$ для всех $n\geqslant 1$, граничный гомоморфизм $\partial \colon \pi _{n+1}(X,A,x_{0})\to \pi _{n}(A,x_{0})$ будет изоморфизмом.

История

Фундаментальная группа была введена создателем топологии Анри Пуанкаре, высшие гомотопические группы — Витольдом Гуревичем. Несмотря на простоту их определения, вычисление конкретных групп (даже для таких простых пространств, как многомерные сферы Sⁿ (смотри гомотопические группы сфер) часто является очень трудной задачей, причём общие методы были получены только в середине XX века с появлением спектральных последовательностей.

Литература

• Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия: Методы и приложения. — М.: Наука, 1979
• Рохлин В. А., Фукс Д. Б. Начальный курс топологии. Геометрические главы. — М.: Наука, 1977
• Свитцер Р. М. Алгебраическая топология — гомотопии и гомологии. — М.: Наука, 1985
• Спеньер Э. Алгебраическая топология. — М.: Мир, 1971
• Фоменко А. Т., Фукс Д. Б. Курс гомотопической топологии. — М.: Наука, 1989