Многоугольник Петри
 Перспектива |
 Развёртка |
 Ортогональная |
 Петри |
 Диаграмма Шлегеля |
 Вершинная фигура |
Многоугольник Петри для правильного многогранника в размерности — это пространственный многоугольник[1], такой что любые последовательных ребра (но не ) принадлежат одной -мерной грани. В частности,
- Многоугольник Петри правильного многоугольника — это сам правильный многоугольник.
- Многоугольник Петри трёхмерного правильного многогранника — это пространственный многоугольник, такой, что любые две последовательные стороны (но не три) принадлежат одной из граней [2].
Для любого правильного многогранника существует ортогональная проекция на плоскость, при которой многоугольник Петри становится правильным многоугольником, содержащим внутри себя все остальные части проекции. При этом плоскость, на которую производится проекция, является плоскостью Коксетера группы симметрии многоугольника, а число сторон является числом Коксетера группы Коксетера. Эти многоугольники и спроецированные графы полезны для показа структур симметрии правильных многогранников большой размерности.
История[править | править код]

Джон Флиндерс Петри (1907—1972) был единственным сыном египтолога Флиндерса Петри[3]. Он родился в 1907 и уже школьником показал замечательные математические способности. При полной концентрации он мог ответить на сложные вопросы о четырёхмерных объектах путём их визуализации.
Он первым обратил внимание на важность правильных пространственных многоугольников, которые возникают на поверхностях правильных многогранников. Коксетер в 1937 объяснил, как он и Петри начали расширять классическое понятие правильных многоугольников:
- Однажды, в 1926, Дж. Ф. Петри сказал мне в большом возбуждении, что он обнаружил два новых правильных многогранника, бесконечных, но без ложных вершин. Когда мой скептицизм начал убывать, он мне их описал — один состоит из квадратов, по шесть в каждой вершине, а другой состоит из шестиугольников, по четыре на вершину [4].
В 1938 Петри, Коксетер, Патрик Дюваль и Х. Т. Флазер выпустили книгу The Fifty-Nine Icosahedra (Пятьдесят девять икосаэдров) [5]. Понимая важность пространственных многогранников, использованных Петри, Коксетер назвал их именем своего друга, когда писал книгу Regular Polytopes (Правильные многогранники).
В 1972, через несколько месяцев после выхода на пенсию, Петри погиб, когда пытался перебежать шоссе рядом со своим домом в графстве Суррей [6].
Идея многоугольников Петри была позднее распространена на полуправильные многогранники.
Многоугольники Петри правильных трёхмерных многогранников[править | править код]
Многоугольник Петри правильного многогранника, имеющего символ Шлефли , имеет сторон, где
- .
Многоугольники Петри двойственных правильных многогранников и имеют подобные проекции.

| ||||
| тетраэдр | куб | октаэдр | додекаэдр | икосаэдр |
| центрирован пр рёбрам | центрирован по вершинам | центрирован по граням | центрирован по граням | центрирован по вершинам |
| 4 стороны | 6 сторон | 6 сторон | 10 сторон | 10 сторон |
| Многоугольники Петри являются внешними границами этих ортогональных проекций. Синим выделены «передние» рёбра, а серым цветом показаны задние рёбра. Концентрические кольца вершин вершин отсчитываются снаружи внутрь с обозначением: , кончая нулём, если нет центральных вершин. | ||||
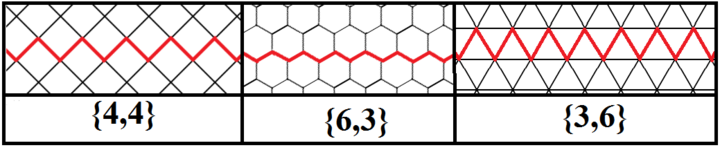
Бесконечные правильные пространственные многоугольники (апейрогоны) можно также определить как многоугольники Петри для правильных мозаик, имеющих углы 90, 120 и 60 градусов (для квадратных, шестиугольных и треугольных граней соответственно).
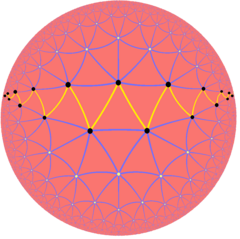
Бесконечные правильные пространственные многоугольники существуют также в качестве многоугольников Петри для правильных гиерболических мозаик, подобных треугольной мозаике порядка 7 {3,7}:
Многоугольники Петри правильных многогранников в четырёхмерном пространстве (4-многогранников)[править | править код]
Можно определить также многоугольники Петри правильных многогранников в четырёхмерном пространстве {p, q ,r}.
 {3,3,3} пятиячейник 5 сторон V:(5,0) |
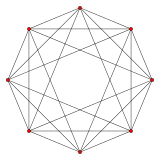 {3,3,4} шестнадцатиячейник 8 сторон V:(8,0) |
 {4,3,3} тессеракт 8 сторон V:(8,8,0) |
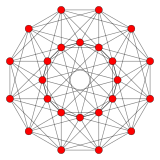 {3,4,3} Двадцатичетырёхъячейник 12 сторон V:(12,6,6,0) |
 {5,3,3} Стодвадцатиячейник 30 сторон V:((30,60)3,603,30,60,0) |
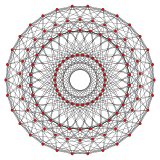 {3,3,5} Шестисотячейник 30 сторон V:(30,30,30,30,0) |
Проекции многоугольников правильных и однородных многогранников размерности 4 и выше[править | править код]
Проекции многоугольников Петри наиболее полезны для визуализации многогранников размерности 4 и выше. Таблица представляет многоугольники Петри трёх семейств правильных многогранников (симплексы, гиперкубы, ортоплексы) и исключительных простых групп Ли En, которые образуют полуправильные и однородные многогранники для размерностей от 4 до 8.
| Семейство n |
n-симплекс | n-гиперкуб | n-ортоплекс | n-полукуб | 1k2 | 2k1 | k21 | пятиугольный многогранник | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Группа | An | BCn |
|
|
Hn | |||||||||||
| 2 |  |
 |
 p-угольник (пример: p=7) |
 Шестиугольник |
 Пятиугольник | |||||||||||
| 3 |  Тетраэдр |
 Куб |
 Октаэдр |
 Тетраэдр |
 Додекаэдр |
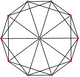 Икосаэдр | ||||||||||
| 4 |  Пятиячейник |
 |
 Шестнадцати- ячейник |
 |
 Двадцати- четырёхъячейник |
 Стодвадцатиячейник |
 Шестисотячейник | |||||||||
| 5 |  Гексатерон |
 Пентеракт |
 5-ортоплекс |
 5-полугиперкуб |
||||||||||||
| 6 |  6-симплекс |
 6-куб |
 6-ортоплекс |
 6-полукуб |
 122 |
 221 |
||||||||||
| 7 |  7-симплекс |
 7-куб |
 7-ортоплекс |
 7-полукуб |
 132 |
 231 |
 321 |
|||||||||
| 8 |  8-симплекс |
 8-куб |
 8-ортоплекс |
 8-полукуб |
 142 |
 241 |
 421 |
|||||||||
| 9 |  8-симплекс |
 9-куб |
 9-ортоплекс |
 9-полукуб |
||||||||||||
| 10 |  10-симплекс |
 10-куб |
 10-ортоплекс |
 10-полукуб |
||||||||||||
Двойственный Петри[править | править код]
Для обсуждения двойственных многоугольников Петри введём понятие схема [7] Неформально, схема P — это семейство многоугольников (которые могут быть бесконечноугольными), такое, что
- Любые два многоугольника имеют общее ребро или вершину, либо не пересекаются вовсе.
- Каждое ребро принадлежит ровно двум многоугольникам.
- Многоугольники, содержащие выбранную вершину, образуют один цикл смежных многоугольников (имеющих общие рёбра).
- Любые два многоугольника связаны цепочкой смежных многоугольников.
Схема P будет иметь группу автоморфизмов Γ (P) и P называется регулярной, если Γ (P) транзитивна на множестве F (P) флагов P. Если регулярная схема P имеет p-угольные грани и q-угольные вершинные фигуры, то говорят, что она имеет (Шлефли) тип {p, q}. Любой правильный многогранник или бесконечногранник порождает регулярную схему естественным образом.
Петри двойственный (Петриал[8]) правильного многогранника — это регулярная схема, вершины и рёбра которой соответствуют вершинам и рёбрам исходного многогранника, а гранями являются множество многоугольников Петри. Эта схема обозначается как оператор π (в виде верхнего индекса) над правильным многогранником. Каждое ребро принадлежит двум граням (многоугольникам Петри) [9][10][11][12].
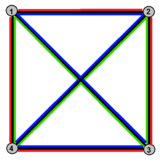
Петриал тетраэдра, {3,3}π, имеет 4 вершины, 6 рёбер и 3 квадратные грани (в виде пространственных квадратов, то есть вершины квадрата не лежат в одной плоскости). Имея эйлерову характеристику χ = 1, петриал топологически идентичен полукубу {4,3}/2.
Петриал куба, {4,3}π, имеет 8 вершин, 12 рёбер и 4 пространственных шестиугольника, показанных красным, зелёным, синим и оранжевым на рисунке. Он имеет эйлерову характеристику 0, и его можно рассматривать как четыре шестиугольные грани тороидальной шестиугольной мозаики {6,3}(2,0).
Петриал октаэдра, {3,4}π, имеет 6 вершин, 12 рёбер и 4 пространственных шестиугольных грани. Петриал имеет эйлерову характеристику −2, и имеет отображение в гиперболическую шестиугольную мозаику 4-го порядка, {6,4}3.
Петриал додекаэдра, {5,3}π, имеет 20 вершин, 30 рёбер и 6 граней в виде пространственных додекаэдров. Его эйлерова характеристика равна −4, и он связан с гиперболической мозаикой {10,3}5.
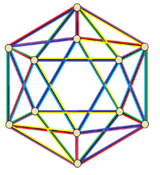
Петриал икосаэдра, {3,6}π, имеет 12 вершин, 30 рёбер и 6 граней в виде пространственных додекаэдров. Его эйлерова характеристика равна −12, и он связан с гиперболической мозаикой {10,5}3.
| Петриал тетраэдра {3,3}π = {4,3}3 = {4,3}/2 |
Петриал куба {4,3}π = {6,3}3 = {6,3}(2,0) |
Петриал октаэдра {3,4}π = {6,4}3 |
Петриал додекаэдра {5,3}π = {10,3}5. |
Петриал икосаэдра {3,5}π = {10,5}3. |
|---|---|---|---|---|
| 3 пространственных квадрата | 4 пространственных шестиугольника | 6 пространственных десятиугольников | ||
|

|

|

|
|
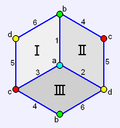 {4,3}3 = {4,3}/2 |
 {6,3}3 = {6,3}(2,0) |
|||
Примечания[править | править код]
- ↑ В английской литературе — skew polygon, буквально — косой многоугольник. В русской литературе прижился термин пространственный многоугольник, а термин косой многоугольник соответствует термину skew polyhedron (косой многогранник).
- ↑ Coxeter, 1995, с. 161, статья 13.
- ↑ Часто встречается также написание фамилии Питри
- ↑ Coxeter, 1937, с. 33-62.
- ↑ Coxeter, 1938, с. 1–26.
- ↑ Coxeter, 1973, с. 32.
- ↑ McMullen, Schulte, 2002, с. 17.
- ↑ От Petrie dual
- ↑ McMullen, Schulte, 2002, с. 192-200.
- ↑ Glossary. Дата обращения: 13 февраля 2016. Архивировано 7 мая 2021 года.
- ↑ Архивированная копия. Дата обращения: 13 февраля 2016. Архивировано 4 марта 2016 года.
- ↑ Coxeter-Petrie Complexes of Regular Maps
Литература[править | править код]
- H.S.M. Coxeter. 2.6 Petrie Polygons стр. 24-25, Chapter 12, стр. 213–235 The generalized Petrie polygon // Regular Polytopes. — 3rd (1947, 63, 73). — New York: Dover Publications Inc., 1973. — ISBN 0-486-61480-8.
- H.S.M. Coxeter. Section 4.3 Flags and Orthoschemes, Section 11.3 Petrie polygons // Regular complex polytopes. — Cambridge, New York: Cambridge University Press, 1973. — ISBN 0-521-39490-2.
- У. Болл, Г. Коксетер. Математические эссе и развлечения. — Москва: «Мир», 1986. — С. 150.
- H.S.M. Coxeter. Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — ISBN 978-0486-40919-8.
- Peter McMullen, Egon Schulte. Abstract Regular Polytopes. — 1st. — Cambridge University Press, 2002. — ISBN 0-521-81496-0.
- H.S.M. Coxeter. Proceedings of the London Mathematical Society. — 1937. — Т. 43. — С. 33-62.
- H.S.M. Coxeter. paper 13, Discrete groups generated by reflections, 1933, стр. 161 // Kaleidoscopes: Selected Writings of H. S. M. Coxeter / F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6.
- H.S.M. Coxeter. The Fifty-nine Icosahedra. — 1938. — С. 1–26. — (University of Toronto studies, mathematical series 6).
Ссылки[править | править код]
- Weisstein, Eric W. Petrie polygon (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Hypercube graphs (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Cross polytope graphs (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. 24-cell graph (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. 120-cell graph (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. 600-cell graph (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Gosset graph 3_21 (англ.) на сайте Wolfram MathWorld.
Для улучшения этой статьи желательно:
|