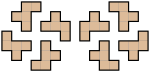
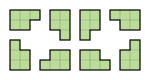
Пентамино

Пентамино́ (от др.-греч. πέντα пять, и домино) — пятиклеточные полимино, то есть плоские фигуры, каждая из которых состоит из пяти одинаковых квадратов, соединённых между собой сторонами («ходом ладьи»). Этим же словом иногда называют головоломку, в которой такие фигуры требуется укладывать в прямоугольник или другие формы.

Виды и количество фигур[править | править код]

Всего существуют 12 различных фигур (элементов) пентамино, обозначаемых латинскими буквами, форму которых они напоминают^[1] (см. рисунок). Считается, что зеркальная симметрия и вращательная симметрия не создают новых фигур. Но если считать и зеркально отражённые фигуры, то их число увеличится до 18. Такое различие имеет значение, например, в компьютерной игре, вариации «Тетриса» — «Пентиксе».

Для составления фигур из пентамино, следует учитывать, что каждая фигура имеет определённое количество инвариантов, другими словами одну и ту же фигуру пентамино можно уложить на игровое поле несколькими способами. Количество инвариантов для всех фигур (кроме фигуры I) пентамино описывается общей формулой : 2^3-cas

где cas - coordinate-axial symmetry – количество координатно-осевых симметрий для расматриваемой фигуры.^[13]

Для проверки количества симметрий, надо совместить центр фигуры пентамино с центром 3-мерной системы координат. Если при повороте на 180^о фигура займёт то же самое положение в пространстве – значит она симметрична относительно данной координатной оси.

Таким образом:

L, N, P, F, Y имеют по 8 инвариантов, поскольку не имеют осей симметрии.
T, V, U, W, Z имеют по 4 инварианта, они имеют по одной (неважно какой) оси симметрии.
I имеет 2 инварианта, хотя имеет 3 оси симметрии, но без учета дублирующих симметрий - только 2.
X имеет все 3 оси симметрии, и следовательно только 1 инвариант.

Отсюда число всех инвариантов пентамино равно 5 × 8 + 5 × 4 + 2 + 1 = 63.

Например, вот восемь инвариантов (возможных способов ориентации) пентамино L, F, P, N и Y:

Составление фигур из пентамино[править | править код]

Укладка прямоугольников[править | править код]

Самая распространённая задача в пентамино — сложить из всех фигурок, без перекрытий и зазоров, прямоугольник. Поскольку каждая из 12 фигур включает в себя 5 квадратов, то прямоугольник должен быть площадью 60 единичных квадратов. Возможны прямоугольники 6×10, 5×12, 4×15 и 3×20. Каждую из этих головоломок можно решить вручную, но более сложной задачей является подсчёт общего числа возможных решений в каждом случае (очевидно, прямоугольники 2 × 30 и 1 × 60 составить из пентамино невозможно, поскольку многие фигуры в них просто не помещаются по ширине).

Для случая 6 × 10 эту задачу впервые решил в 1965 году Джон Флетчер^[2]. Существует 2339 различных укладок пентамино в прямоугольник 6×10, не считая поворотов и отражений целого прямоугольника, но считая повороты и отражения его частей (иногда внутри прямоугольника образуется симметричная комбинация фигур, поворачивая которую, можно получить дополнительные решения; для прямоугольника 3×20, приведённого на рисунке, второе решение можно получить поворотом блока из 7 фигур, или, иначе говоря, если поменять местами четыре фигуры, крайние слева, и одну крайнюю справа).

Для прямоугольника 5 × 12 существует 1010 решений, 4 × 15 — 368 решений, 3 × 20 — всего 2 решения (отличающихся вышеописанным поворотом). В частности, существует 16 способов сложить два прямоугольника 5 × 6, из которых можно составить как прямоугольник 6 × 10, так и 5 × 12.

Укладка прямоугольников из односторонних пентамино[править | править код]

Если дополнить набор пентамино зеркальными копиями фигур, не совпадающих со своими отражениями (F, L, P, N, Y и Z), то из полного набора в 18 односторонних пентамино можно сложить прямоугольники площадью 90 единичных квадратов (при этом фигуры не разрешается переворачивать). Задача о составлении прямоугольника 3 × 30 имеет 46 решений, 5 × 18 — более 600 тыс. решений, 6 × 15 — более 2 млн решений и 9 × 10 — более 10 млн решений^[3].

Укладка фигур с отверстиями[править | править код]

В какой-то степени более простую (более симметричную) задачу, для квадрата 8×8 с отверстием в центре 2×2, решил еще в 1958 году Дана Скотт^[4] (аспирант-математик Принстона). Для этого случая существует 65 решений. Алгоритм Скотта был одним из первых применений компьютерной программы поиска с возвратом.

Другой вариант этой головоломки — выкладывание квадрата 8×8 с 4 отверстиями в произвольно заданных местах. Большинство таких задач имеют решение. Исключением являются случаи с размещением двух пар отверстий вблизи двух углов доски так, чтобы в каждый угол можно было поместить только P-пентамино, или всех четырёх отверстий вблизи одного угла так, что при любом возможном заполнении угловой клетки (с помощью U- или T-пентамино) от доски отсекается ещё одна клетка (см. рисунок).

Для решения этих задач эффективные алгоритмы описал, например, Дональд Кнут^[5]^[6]. На современном компьютере подобные головоломки решаются за считанные секунды.

Укладка фигур животных, предметов и техники[править | править код]

Из головоломки можно выкладывать животных, птиц и рыб, а также растения, различные предметы и технику. Используются при этом как все 12 элементов пентамино, так и их часть.

Задача об утроении фигур пентамино[править | править код]

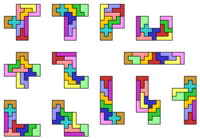
Эта задача была предложена профессором Калифорнийского университета Р.М.Робинсоном. Выбрав одну из 12 фигур пентамино, необходимо построить из каких-либо 9 из 11 оставшихся пентамино фигуру, подобную выбранной, но в масштабе 3:1 (втрое больше). Решение существует для любого из 12 пентамино, причём не единственное (от 15 решений для Х до 497 для Р)^[3]. Существует вариант этой задачи, в котором для построения утроенной фигуры разрешается использовать также и саму исходную фигуру. В этом случае число решений от 20 для Х до 9144 для Р-пентамино^[7].

Представленное на рисунке решение^[8], найденное А.ван де Ветерингом, обладает интересным свойством: каждое пентамино используется для утроения девяти из остальных, по одному разу в каждой. Таким образом, из 9 комплектов исходных фигур пентамино можно одновременно сложить все 12 утроенных пентамино.

Настольная игра[править | править код]

Пентамино может использоваться также как настольная игра для двух игроков^[9]. Для игры необходима шахматная доска 8×8 и набор фигур пентамино, клетки которых имеют одинаковый размер с клетками доски. В начале игры доска пуста. Игроки поочерёдно выставляют на доску по одной фигуре, закрывая 5 свободных клеток доски. Все выставленные фигуры остаются на месте до конца партии (не снимаются с доски и не передвигаются). Проигравшим считается игрок, который первым не сможет сделать хода (либо из-за того, что ни одна из оставшихся фигур не умещается на свободных участках доски, либо потому, что все 12 фигур уже выставлены на доску).

Анализ игры достаточно сложен (так, в начале имеется даже больше возможных первых ходов, чем в шахматах). Голомб предложил следующую стратегию: стремиться разбить свободное место на доске на два равновеликих участка (и помешать сопернику сделать это). После этого на каждый ход соперника на одном из участков следует отвечать ходом на другом.

Партия в игре пентамино для двух игроков

Пример партии в пентамино показан на рисунке. Нумерация ходов сквозная (нечётные номера ходов принадлежат первому игроку, чётные — второму). Первоначально игроки делают ходы в центре доски (ходы 1—3), не позволяя друг другу разбить доску на равновеликие участки. Но затем второй игрок делает неудачный ход (4), позволяющий сопернику разбить свободное место на два участка по 16 клеток (ход 5). (В этом примере свободные участки не только равны по площади, но и совпадают по форме — симметричны относительно диагонали доски, но для стратегии это, разумеется, не обязательно.) Далее на ход второго игрока (6) на одном из этих участков первый игрок отвечает ходом на другом (7) и выигрывает. Хотя на доске ещё есть три свободных участка в пять и более клеток, но все подходящие фигуры (I, P, U) уже использованы.

Варианты настольной игры[править | править код]

Пентамино с заранее выбранными фигурами[править | править код]

В этом варианте игры игроки сначала по очереди выбирают по одной фигуре, пока все фигуры не будут распределены между ними. Далее игра проходит по правилам обычного пентамино, с той разницей, что каждому из игроков разрешается ходить только теми фигурами, которые он выбрал. Взявший последнюю фигуру делает первый ход.

Стратегия этого варианта игры, предложенная Голомбом, существенно отличается от стратегии обычного пентамино. Вместо того, чтобы разбить доску на равновеликие участки, игрок стремится создать на доске участки, которые можно заполнить лишь его фигурами, но не фигурами соперника. (Голомб называет такие участки «убежищами».)

Пример партии в пентамино с заранее выбранными фигурами показан на рисунке. Фигуры, выбранные первым и вторым игроками, перечислены слева и справа от доски соответственно. Зачёркнутая буква обозначает, что фигура использована для хода. Сначала игроки избавляются от самых «неудобных» фигур X и W (ходы 1 и 2). Затем первый игрок создаёт «убежище» для фигуры Y (ход 3), второй — для фигур U и P (ходы 4 и 6). В конце партии (ходы 8—10) происходит заполнение этих «убежищ» и партия заканчивается победой второго игрока — у первого остаётся Т-образное пентамино, для которого на оставшейся части доски нет подходящего места.

Другие варианты[править | править код]

«Карточное пентамино» — вариант игры с привнесением случайных событий. Фигуры пентамино (или их буквенные обозначения) рисуют на карточках, которые тасуют и раздают игрокам. Игроки выбирают фигуры в соответствии с розданными им карточками. Далее игра идёт по правилам пентамино с заранее выбранными фигурами.
Пентамино для четырёх игроков. Четыре игрока, сидящие по четырём сторонам доски, играют двое на двое (игроки, сидящие друг напротив друга, образуют команду). Проигравшей считается команда, игрок которой первым не сможет сделать хода. В эту игру можно играть по любому из трёх вышеописанных вариантов — обычному, с заранее выбранными фигурами или «карточному».
«Кто-кого?» В игре участвует от двух до четырёх игроков, но каждый из них играет только за себя. Победителем считается сделавший последний ход, ему засчитывается 10 очков. Игрок, который должен ходить после победителя (т.е. первым не сможет сделать хода), получает 0 очков, а все остальные игроки — по 5 очков. Может быть сыграно несколько партий, набранные в них очки суммируются. Игра также может проводиться по любому из трёх вышеописанных вариантов правил.

Компьютерные игры[править | править код]

С конца 1980-х годов неоднократно выходили различные компьютерные игры, основанные на пентамино. Наиболее известная — основанная на идее «Тетриса» игра «пентикс» (Pentix). Один из новейших примеров — игра Dwice, которую разработал в 2006 году изобретатель «Тетриса» Алексей Пажитнов.