Задача Иосифа Флавия: различия между версиями
| [отпатрулированная версия] | [отпатрулированная версия] |
м →История: орфография, пунктуация |
м →Пример: орфография |
||
| Строка 109: | Строка 109: | ||
| [[Файл:Program1.GIF|400]] |
| [[Файл:Program1.GIF|400]] |
||
|- |
|- |
||
! Рис 1. Круг из 10 |
! Рис 1. Круг из 10 солдат, в котором |
||
|- |
|- |
||
! должен «умереть» каждый второй |
! должен «умереть» каждый второй |
||
| Строка 139: | Строка 139: | ||
! Рис. 5 — 1-й этап при количестве солдат в круге 2n |
! Рис. 5 — 1-й этап при количестве солдат в круге 2n |
||
|} |
|} |
||
Наблюдается аналогичная ситуация и при 2n |
Наблюдается аналогичная ситуация и при 2n − 1 — солдатах на входе (рис.6). Однако вводится поправка- уменьшение на единицу и увеличение F(n) в 2 раза. |
||
{| class="wikitable" |
{| class="wikitable" |
||
| Строка 148: | Строка 148: | ||
|} |
|} |
||
Из чего можно вывести формулу F(2n) = 2 |
Из чего можно вывести формулу F(2n) = 2 F(n) − 1 (для всех n > 1). |
||
Рассмотрим случай № 2, приняв во внимание тот факт, что на вход подаются 2n + 1 число солдат (то есть нечетное количество солдат). После проведения 1-го этапа «исключения» солдат из круга получится нечто, приведенное на рис.7. |
Рассмотрим случай № 2, приняв во внимание тот факт, что на вход подаются 2n + 1 число солдат (то есть нечетное количество солдат). После проведения 1-го этапа «исключения» солдат из круга получится нечто, приведенное на рис.7. |
||
{| class="wikitable" |
{| class="wikitable" |
||
| Строка 156: | Строка 156: | ||
! Рис. 7 — 1-й этап при количестве солдат в круге 2n + 1 |
! Рис. 7 — 1-й этап при количестве солдат в круге 2n + 1 |
||
|} |
|} |
||
Из чего можно вывести формулу F(2n +1) = 2 |
Из чего можно вывести формулу F(2n +1) = 2 F(n) + 1 (для всех n > 1). |
||
Сведем все рассмотренные ситуации и запишем все случаи в виде системы, позволяющей определить значение функции F(n) — для любых значений n: |
Сведем все рассмотренные ситуации и запишем все случаи в виде системы, позволяющей определить значение функции F(n) — для любых значений n: |
||
{| class="wikitable" |
{| class="wikitable" |
||
| Строка 164: | Строка 164: | ||
Выведенные выше формулы могут быть применены и для решения исходной задачи — Иосифа Флавия. |
Выведенные выше формулы могут быть применены и для решения исходной задачи — Иосифа Флавия. |
||
А именно: |
А именно: |
||
F(2 |
F(2<sup>m</sup> + k) = 2k + 1 для любого m любого k. |
||
=== Представление решения для случая убийства каждого 2-го через двоичную запись === |
=== Представление решения для случая убийства каждого 2-го через двоичную запись === |
||
Версия от 18:12, 19 января 2021
Задача Иосифа Флавия — задача, входящая в одну из ранних работ по занимательной математике (1612 года) Баше де Мезириака. Задача заключается в следующем: по кругу стоит 41 воин, начиная с первого воина они убивают каждого третьего. Спрашивается, в каком месте нужно встать, чтобы остаться последним выжившим. В более общей формулировке участвует n воинов, которые считаются по кругу, и убивают каждого m-го. Название задачи восходит к истории, случившейся с Иосифом Флавием во время Иудейской войны.
История
Эта задача известна с 1612 года, когда французский математик Баше опубликовал эту задачу в своём сборнике Problem es Plaisants. Сюжет задачи основан на истории, описанной Иосифом Флавием в своём историческом труде «Иудейская война».
Согласно этой истории, Иосиф Флавий со своим отрядом из сорока человек после падения Йодфата скрылся в пещере, но был обнаружен римлянами. Все в отряде, кроме Иосифа, предпочли совершить самоубийство, но не сдаваться в плен. Иосиф пытался отклонить своих товарищей от самоубийства. Однако они обвиняли его в трусости и хотели убить своего командира. Далее Иосиф (говоря о себе в третьем лице) пишет:
И в этом тяжёлом положении Иосифа не покинуло его благоразумие: в надежде на милость Божию он решил рискнуть своей жизнью и сказал: «Раз решено умереть, так давайте предоставим жребию решить, кто кого должен убивать. Тот, на кого падёт жребий, умрёт от рук ближайшего за ним, и таким образом мы все по очереди примем смерть один от другого и избегнем необходимости сами убивать себя; будет, конечно, несправедливо, если после того, как другие уже умрут, один раздумает и останется в живых». Этим предложением он вновь возвратил себе их доверие; уговорив других, он сам также участвовал с ними в жребии. Каждый, на которого пал жребий, по очереди добровольно дал себя заколоть другому, последовавшему за ним товарищу, так как вскоре за тем должен был умереть также и полководец, а смерть вместе с Иосифом казалась им лучше жизни. По счастливой ли случайности, а быть может по божественному предопределению, остался последним именно Иосиф ещё с одним. А так как он не хотел ни самому быть убитым по жребию, ни запятнать свои руки кровью соотечественника, то он убедил и последнего сдаться римлянам и сохранить себе жизнь.Иосиф Флавий. Иудейская война, книга 3, глава 8, 7
В задаче Баше солдаты не бросают жребий, а встают по кругу и убивают каждого третьего. В этом случае у Иосифа появляется возможность не полагаться на волю случая, а гарантировано спастись. Боше спрашивает, где нужно встать Иосифу и его товарищу, чтобы остаться последними, на кого выпадет жребий[1].
Задача вдохновила Станислава Улама на создания понятия счастливого числа[1].
На решении задачи Иосифа для основан фокус «Love Ritual»[2], созданный испанским фокусником Вуди Арагоном, который показывают Пенн и Теллер[3].
Рекуррентные соотношения
Если известно решение задачи для некоторого числа воинов, то его можно использовать для решения задачи с на единицу большим числом воинов.
Для имеем
Для имеем
Очевидно для общего случая будем иметь
Возможно построение рекуррентных соотношений, которые сходятся намного быстрее чем линейные. Вот пример решения задачи для с логарифмическим числом шагов рекурсии:
Замкнутая формула
При программировании приведенные выше рекуррентные соотношения дают вычислительную сложность и соответственно. Получение решения в замкнутой форме должно приводить к алгоритмам в которых вычислительная сложность минимальна — , т. е. вообще не зависит от и . (Длина записи представления чисел в системе счисления не учитывается). Построение таких формул крайне желательно и для данной задачи.
Для существует простая формула:
Способы решения
Переборное решение
Рассмотрим ещё два способа решения задачи, не опирающихся на приведенную выше формулу. Несмотря на то, что они сложнее для вычисления в плане вычислительной скорости, все же, алгоритм более нагляден. Давайте повторим в ОЗУ события, происходившие в легенде.
Способ первый
Будем хранить в массиве имена (то есть номера) всех живых на текущий момент воинов. Причем удобно, чтобы номера людей были записаны в элементах массива с 0 по N — 1 (это свойство будет использоваться для операции взятия остатка). Когда воин будет умирать, будем удалять его из массива, и тех, кто стоял за ним, «сдвигать» на один элемент влево.
Заметим, что если мы уже убили L человек, то в живых осталось M = N — L. Пусть мы только что (на L-ом шаге) убили человека, который был записан в нашем массиве в элементе с номером j (и сдвинули людей, которые были записаны в массиве в элементах с j + 1 по M на один элемент влево). Тогда следующим нужно убивать человека, который записан в этом массиве в элементе с номером (j + k — 1) % M.
Способ второй
Заведем массив, где будем помечать мертвых воинов (то есть в i-м элементе хранится, жив воин i, или уже нет). Пусть у нас на текущем шаге M живых людей и на предыдущем шаге умер воин j. Чтобы найти следующего, будем бежать по массиву, отсчитывая живых и пропуская мертвых. Тот человек, на котором мы насчитаем k % M и должен умереть следующим. Через N — 1 шаг останется один человек.
Рекурсивное решение
Простейшее моделирование будет работать O (). Используя дерево отрезков, можно произвести моделирование за . Однако попытаемся найти закономерность, выражающую ответ для задачи (N,K) через решение предыдущих задач. С помощью моделирования построим таблицу значений, скажем, приведенную ниже.
Таблица
1
2
3
4
5
6
7
8
9
10
1
1
1
1
1
1
1
1
1
1
1
2
2
1
2
1
2
1
2
1
2
1
3
3
3
2
2
1
1
3
3
2
2
4
4
1
1
2
2
3
2
3
3
4
5
5
3
4
1
2
4
4
1
2
4
6
6
5
1
5
1
4
5
3
5
2
7
7
7
4
2
6
3
5
4
7
5
8
8
1
7
6
3
1
4
4
8
7
9
9
3
1
1
8
7
2
3
8
8
10
10
5
4
5
3
3
9
1
7
8
И здесь достаточно отчётливо видна следующая закономерность:
joseph (n, k) = ( joseph (n-1, k) + k - 1 ) % n + 1;
joseph (1, k) = 1
(здесь индексация с единицы несколько портит элегантность формулы)
Итак, мы нашли решение задачи Иосифа Флавия, работающее за итераций.
Пример
С целью подробного объяснения возможных ситуаций, которые могут возникнуть в ходе решения, упростим исходную задачу и рассмотрим случай № 1, причем, уменьшим круг солдат с сорока одного (сорок солдат и Иосиф) до десяти и предположим, что вместо каждого третьего солдата должен умереть каждый второй. В результате будем рассматривать круг солдат, изображенный на рис 1.
| Рис 1. Круг из 10 солдат, в котором |
|---|
| должен «умереть» каждый второй |
Если производить отсчет от 1-го солдата в круге, то порядок удаления будет следующим: 2, 4, 6, 8, 10, 3, 7, 1, 9. Солдат под номером 5 — в конечном итоге остается в живых.
Этапы «уничтожения» солдат из круга графически представлены на рис 2 — 4.
| Рис 2. 1-й этап удаления | Рис 3. 2-й этап удаления | Рис 4. 3-й этап удаления |
|---|
Рассмотрим конкретную ситуацию и определим результаты, используя предопределенные условия. Задача состоит в том, чтобы установить зависимости между параметрами k, n (где n — это количество людей в круге, k — служит для определения каждого k-го солдата для «исключения» из круга), и решить задачу независимо от того, сколько солдат стоят в круге. Попробуем вывести общие формулы для решения задачи с любыми входными параметрами (на вход подаются значения k и n). Для этого определяем функцию F(n), где F(n) — возвращает номер победителя. Сразу возникает первое предположение, что F(n) может быть в пределах F(n) = n / 2, что верно при n = 10 или n = 2. Однако при n = 4 F(4) = 1, что доказывает неправильность рассуждений. Следующее замечание из рассмотренной выше ситуации: полученный результат — нечетный номер, независимо от значения n, так произошло вследствие того, что в ходе 1-го этапа — были убраны все четные номера. Также следует учесть тот факт, что при n = 1 F(1) = 1. Предположив, что на входе солдат = 2n. То, что остается после 1-го этапа показано на рис. 5.
| Рис. 5 — 1-й этап при количестве солдат в круге 2n |
|---|
Наблюдается аналогичная ситуация и при 2n − 1 — солдатах на входе (рис.6). Однако вводится поправка- уменьшение на единицу и увеличение F(n) в 2 раза.
| Рис. 6. солдат в круге 2n — 1 |
|---|
Из чего можно вывести формулу F(2n) = 2 F(n) − 1 (для всех n > 1). Рассмотрим случай № 2, приняв во внимание тот факт, что на вход подаются 2n + 1 число солдат (то есть нечетное количество солдат). После проведения 1-го этапа «исключения» солдат из круга получится нечто, приведенное на рис.7.
| Рис. 7 — 1-й этап при количестве солдат в круге 2n + 1 |
|---|
Из чего можно вывести формулу F(2n +1) = 2 F(n) + 1 (для всех n > 1). Сведем все рассмотренные ситуации и запишем все случаи в виде системы, позволяющей определить значение функции F(n) — для любых значений n:
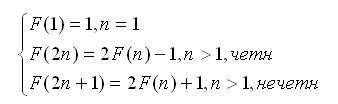
|
Выведенные выше формулы могут быть применены и для решения исходной задачи — Иосифа Флавия. А именно: F(2m + k) = 2k + 1 для любого m любого k.
Представление решения для случая убийства каждого 2-го через двоичную запись
Рассмотрим двоичные представлениям величин n и F(n): , где каждое равно 0 или 1, причем старший бит равен 1. Вспоминая, что , последовательно получаем:
(так как )
(так как )
(так как и )
Таким образом, мы получили, что
- ,
то есть F(n) получается путём циклического сдвига двоичного представления n влево на одну позицию.
Примечания
- ↑ 1 2 Dowdy, James; Mays, Michael E. Josephus permutations (англ.) // Journal of Combinatorial Mathematics and Combinatorial Computing. — 1989. — October (vol. 6). — P. 125—130.
- ↑ Penn & Teller Fool Us - Can you find the Love? на YouTube 2016.
- ↑ Ricardo Teixeira, Jang-Woo Park. An Innovative Card Trick that Combines Classical Concepts (англ.) // Recreational Mathematics Colloquium VI G4G Europe. — 2019. — January. — P. 11.
Литература
- М. А. Алексеев. Задача Иосифа Флавия // Империя Математики. — 2001. — № 2. — С. 22—28.
- Дональд Кнут, Роналд Грэхем, Орен Паташник. Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7.




























