Параметрическое представление

Пример параметрической кривой.

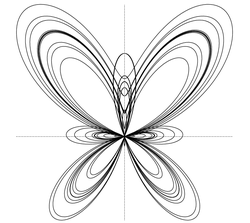
Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную величину — параметр.

Параметрическое представление функции

Предположим, что функциональная зависимость y от x не задана непосредственно y = f(x), а через промежуточную величину — t. Тогда формулы

$x=\varphi (t)~;$  $y=\psi (t)$

задают параметрическое представление функции одной переменной.

Если предположить, что обе эти функции φ и ψ имеют производные и для φ существует обратная функция θ, явное представление функции выражается через параметрическое как:

$y=\psi (\theta (x))=f(x)$

и производная функции может быть вычислена как

$y'(x)={\frac {dy}{dx}}={\frac {y'_{t}}{x'_{t}}}={\frac {\psi '(t)}{\phi '(t)}}$

Параметрическое представление даёт такое важное преимущество, что позволяет изучать неявные функции в тех случаях, когда их приведение к явному виду иначе как через параметры затруднительно.

Параметрическое представление уравнения

Параметрическое представление для более общего случая: когда переменные связаны уравнением (или системы уравнений, если переменных больше двух).

Параметрическое уравнение

Близкое понятие — параметрическое уравнение множества точек, когда координаты точек задаются как функции от некоторых набора свободных параметров. Если параметр один, мы получим параметрическое уравнение кривой.

$x=x(t);y=y(t)$ (кривая на плоскости),

$x=x(t);y=y(t);z=z(t)$ (кривая в 3-мерном пространстве),

Выражая координаты точек поверхности через два свободных параметра, мы получим параметрическое задание поверхности.

Примеры

Уравнение окружности имеет вид:

$x^{2}+y^{2}=r^{2}.$

Параметрическое уравнение окружности:

$x=r~\cos ~t~;$

$y=r~\sin ~t~;~~0\leq t<2\pi$

Гипербола описывается следующим уравнением:

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1.$

Параметрическое уравнение правой ветви гиперболы :

$x=a~\operatorname {ch} ~t$$;~y=b~\operatorname {sh} ~t~;~~-\infty <t<+\infty$

См. также

• Параметрическое задание поверхности

Ссылки

• Параметрическое задание кривой. Лекции по математическому анализу
• Лекции по математическому анализу. доцент кафедры математического анализа Иркутского госуниверситета Романова О. А.