Теорема Вариньона (геометрия)

Красный четырёхугольник — параллелограмм

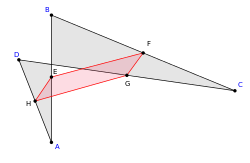
Теоре́ма Вариньо́на — геометрический факт, доказанный Пьером Вариньоном и утверждающий, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма:

Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.

Параллелограмм, образованный серединами сторон, иногда называется вариньоновским или вариньоновым.

Следствия

• Центр параллелограмма Вариньона лежит на середине отрезка, соединяющего середины сторон исходного четырёхугольника (в этой же точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).
• Периметр параллелограмма Вариньона равен сумме диагоналей исходного четырёхугольника.
• Площадь параллелограмма Вариньона равна половине площади исходного четырёхугольника.
• Для прямоугольника и равнобедренной трапеции параллелограммом Вариньона является ромб, а для ромба — прямоугольник.
• Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны 2) бимедианы перпендикулярны.
• Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: 1) диагонали перпендикулярны; 2) бимедианы равны.
• Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны и перпендикулярны; 2) бимедианы равны и перпендикулярны.

Доказательство

Доказательство, что площадь параллелограмма равна половине площади исходного четырёхугольника

Пусть диагональ $AC$ проходит внутри четырёхугольника. Тогда площадь треугольника $ABC$ равна ${\frac {AC\cdot h_{b}}{2}}$, где $h_{b}$ --- высота треугольника $ABC$, проведённая из вершины $B$. Аналогично, площадь треугольника $ADC$ равна ${\frac {AC\cdot h_{d}}{2}}$. Тогда площадь всего четырёхугольника равна ${\frac {AC(h_{b}+h_{d})}{2}}$. Но ${\frac {(h_{b}+h_{d})}{2}}={\frac {h_{b}}{2}}+{\frac {h_{d}}{2}}$ — это сумма расстояний до прямой $AC$ от точек $E$ и $H$, то есть в точности высота параллелограмма $EHGF$. А поскольку сторона $GH$ параллелограмма вдвое меньше $AC$, то и площадь параллелограмма равна половине площади $ABCD$, Q. E. D.

выпуклый четырёхугольник	невыпуклый четырёхугольник	самопересекающийся четырёхугольник

См. также

• Прямая Ньютона
• Теорема Ньютона (планиметрия)
• Четырехугольник