Плосконосая тришестиугольная мозаика
| Плосконосая тришестиугольная мозаика | |
|---|---|

| |
| Тип | полуправильная мозаика |
| Конфигурация вершины |
 3.3.3.3.6 |
| Символ Шлефли | sr{6,3} или |
| Символ Витхоффа |
| 6 3 2 |
| Диаграмма Коксетера — Дынкина |
|
| Симметрии | p6, [6,3]+, (632) |
| Симметрии вращения | p6, [6,3]+, (632) |
| Обозначение Бауэрса | Snathat |
| Двойственная мозаика |
Цветочная пятиугольная мозаика |
| Свойства | вершинно транзитивная хиральная |
Плосконосая шестиугольная мозаика (или плосконосая тришестиугольная мозаика) — это полуправильная мозаика на евклидовой плоскости. В каждой вершине имеется четыре треугольника и один шестиугольник. Мозаика имеет символ Шлефли sr{3,6}. Плосконосая четырёхшестиугольная мозаика связана с гиперболической мозаикой с символом Шлефли sr{4,6}.
Конвей назвал мозаику snub hextille (плосконосый шестипаркет), построенной с помощью операции отсечения углов и применённой к шестиугольному паркету (hextille).
Существует на плоскости 3 правильные и 8 полуправильных мозаик. Только одна не имеет отражения в качестве симметрии.
Существует только одна однородная раскраска плосконосой тришестиугольной мозаики (а именно, раскраска с индексами (3.3.3.3.6): 11213.)
Упаковка окружностей[править | править код]
Плосконосая тришестиугольная мозаика может быть использована как упаковка кругов, если разместить круги одинакового радиуса с центром в каждой вершине. Любая окружность соприкасается с 5 другими окружностями упаковки (контактное число)[1]. Область решётки (красный ромб) содержит 6 различных окружностей. Шестиугольные дыры могут быть заполнены в точности одной окружностью, что приводит к плотной упаковке окружностей.
Связанные многогранники и мозаики[править | править код]

| Однородные шестиугольные/треугольные мозаики | ||||||||
|---|---|---|---|---|---|---|---|---|
| Фундаментальные домены |
Симметрия: [6,3], (*632) | [6,3]+, (632) | ||||||
| {6,3} | t{6,3} | r{6,3} | t{3,6} | {3,6} | rr{6,3} | tr{6,3} | sr{6,3} | |

|

|

|

|

|

|

|

|

|
| Конфиг. | 63 | 3.12.12 | (6.3)2 | 6.6.6 | 36 | 3.4.6.4 | 4.6.12 | 3.3.3.3.6 |
Варианты симметрии[править | править код]
Эта полуправильная мозаика является членом последовательности усечённых многогранников и мозаик с вершинной фигурой (3.3.3.3.n) и диаграммой Коксетера — Дынкина ![]()
![]()
![]()
![]()
![]() . Эти фигуры и их двойственные имеют (n32) вращательную симметрию и являются мозаикой в евклидовой плоскости для n=6 и в гиперболической плоскости для всех больших n. Серию можно считать начинающейся с n=2 с одним набором граней, вырожденных в двуугольники.
. Эти фигуры и их двойственные имеют (n32) вращательную симметрию и являются мозаикой в евклидовой плоскости для n=6 и в гиперболической плоскости для всех больших n. Серию можно считать начинающейся с n=2 с одним набором граней, вырожденных в двуугольники.
| Симметрия n32 |
Сферическая | Евклидоваn | Компактная гиперболич. | Паракомп. | ||||
|---|---|---|---|---|---|---|---|---|
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Плосконосые фигуры |

|

|

|

|

|

|

|

|
| Конфигурация | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Фигуры | 
|

|

|

|

|

|

| |
| Конфигурация | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |
Цветочная пятиугольная мозаика[править | править код]
| Цветочная пятиугольная мозаика | |
|---|---|

| |
| Тип | Мозаика, двойственная полуправильной мозаике |
| Список граней | неправильные пятиугольники |
| Конфигурация граней |
V3.3.3.3.6 |
| Диаграмма Коксетера — Дынкина |
|
| Симметрии | p6, [6,3]+, (632) |
| Симметрии вращения | p6, [6,3]+, (632) |
| Двойственная мозаика |
Плосконосая тришестиугольная мозаика |
| Свойства | гране транзитивная хиральная |
Цветочная пятиугольная мозаика или розеточная пятиугольная мозаика является двойственной полуправильной мозаикой евклидовой плоскости. Это одна из 15 известных изоэдральных пятиугольных мозаик. Название мозаика получила за сходство шести пятиугольных плиток на цветок, лепестки которого расходятся из центральной точки[2]. Конвей назвал эту мозаику 6-fold pentille (6-кратный пятипаркет)[3]. Каждая грань мозаики имеет четыре угла 120° и один угол 60°.
Мозаика является двойственной для (однородной) плосконосой тришестиугольной мозаики[4] и имеет вращательную симметрию порядка 6-3-2.
Вариации[править | править код]
Цветочная пятиугольная мозаика имеет геометрические вариации с неравными длинами сторон и вращательной симметрией, которая является моноэдральной пятиугольной мозаикой типа 5. В одном из пределов длина ребра стремится к нулю и мозаика становится дельтоидной тришестиугольной мозаикой.
 (См. анимацию) |
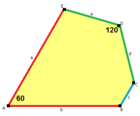 a=b, d=e A=60°, D=120° |
 Дельтоидная тришестиугольная мозаика |
 a=b, d=e, c=0 60°, 90°, 90°, 120° |
Связанные мозаики[править | править код]
| Симметрия: [6,3], (*632) | [6,3]+, (632) | |||||
|---|---|---|---|---|---|---|

|

|

|

|

|

|

|
| V63 | V3.122 | V(3.6)2 | V36 | V3.4.6.4 | V.4.6.12 | V34.6 |
См. также[править | править код]
Примечания[править | править код]
- ↑ Critchlow, 1970, с. 74—75, pattern E.
- ↑ Five space-filling polyhedra Архивная копия от 6 апреля 2013 на Wayback Machine by Guy Inchbald
- ↑ Conway, Burgiel, Goodman-Strass, 2008, с. 288.
- ↑ Weisstein, Eric W. Dual tessellation (англ.) на сайте Wolfram MathWorld.
Литература[править | править код]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. Chapter 19, The Hyperbolic Archimedean Tessellations, Chapter 21, Naming Archimedean and Catalan polyhedra and tilings // The Symmetries of Things. — 2008. — С. 288 table. — ISBN 978-1-56881-220-5. Архивная копия от 19 сентября 2010 на Wayback Machine
- B. Grünbaum, G.C. Shephard. list of 107 isohedral tilings // Tilings and Patterns. — New York: W. H. Freeman & Co., 1987. — С. 473—481. — ISBN 0-7167-1193-1.
- Williams R. The Geometrical Foundation of Natural Structure: A Source Book of Design. — New York: Dover Publications, 1979. — С. 32. — ISBN 0-486-23729-X.
- Keith Critchlow. Order in Space: A design source book. — Thames & Hudson, 1970. — ISBN 0-500-34-033-1. Переиздание 2000
- Dale Seymour, Jill Britton. Introduction to Tessellations. — Palo Alto: Dale Seymour Publications, 1989. — С. 50—56. — ISBN 978-0866514613.
Ссылки[править | править код]
- Weisstein, Eric W. Uniform tessellation (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Semiregular tessellation (англ.) на сайте Wolfram MathWorld.
- Richard KlitzingP 2D Euclidean tilings s3s6s — snathat — O11 Архивная копия от 9 декабря 2017 на Wayback Machine
Для улучшения этой статьи желательно:
|



