Дедекиндово сечение
Дедеки́ндово сече́ние — один из способов построения вещественных чисел из рациональных[1].
Множество вещественных чисел определяется как множество дедекиндовых сечений. На них возможно продолжить операции сложения и умножения.
История[править | править код]
Метод был введён в 1872 году Рихардом Дедекиндом[2][3].
Аналогичное построение для геометрических величин неявно присутствует в «Началах» Евклида, а именно, в книге V определение 5 звучит следующим образом:
Говорят, что величины находятся в том же отношении первая ко второй и третья к четвёртой, если равнократные первой и третьей одновременно больше, одновременно равны или одновременно меньше равнократных второй и четвёртой каждая каждой при какой бы то ни было кратности, если взять их в соответствующем порядке (9, 10, 11, 12).[4].
Близкие идеи опубликовал в 1849 году французский математик Жозеф Бертран[5].
Определение[править | править код]
Дедекиндово сечение — это разбиение множества рациональных чисел на два подмножества (нижнее, или левое) и (верхнее, или правое) такие, что[6]:
- для любых и ,
- не имеет наименьшего элемента.
Далее дедекиндово сечение обозначается (хотя было бы достаточно указать одно из этих множеств, второе дополняет его до ).
Если множество имеет наибольший элемент, то дедекиндово сечение можно отождествить с этим рациональным числом. В противном случае сечение определяет иррациональное число, которое больше всех чисел множества и меньше всех чисел множества . Определив на полученном множестве сечений арифметические операции и порядок, мы получаем поле вещественных чисел, причём каждое сечение определяет одно и только одно вещественное число.
Пример[править | править код]
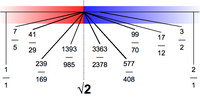
Вещественному числу соответствует дедекиндово сечение, для которого[7]:
- множество
- множество
Интуитивно можно представить себе, что для того, чтобы определить , мы рассекли множество на две части: все числа, что левее , и все числа, что правее ; соответственно, равен точной нижней грани множества .
Упорядоченность дедекиндовых сечений[править | править код]
Введём во множестве сечений порядок. Сначала определим, что два сечения и равны, если (тогда и ). Далее определим[8]:
- , если и при этом
Нетрудно проверить, что все требования линейного порядка выполнены. Кроме того, для рациональных чисел новый порядок совпадает со старым.
Из данного определения порядка следует:
- Теорема о приближении. Любое вещественное число может быть с любой точностью приближено рациональными числами, то есть может быть заключено в интервал с рациональными границами произвольно малой длины[9].
Арифметика дедекиндовых сечений[править | править код]
Для определения арифметических действий с сечениями можно воспользоваться сформулированной в предыдущем разделе теоремой о приближении.
Пусть — вещественные числа. Согласно теореме о приближении, для них можно указать интервалы-приближения с рациональными границами:
Тогда суммой называется[10] вещественное число, содержащееся во всех интервалах вида Сумма вещественных чисел всегда существует, однозначно определена и для рациональных чисел совпадает с прежним определением суммы. Вычитание всегда возможно, поэтому относительно так определённой операции сложения вещественные числа образуют аддитивную группу.
Аналогично определяется умножение вещественных чисел, которое вместе со сложением превращает множество вещественных чисел в упорядоченное поле[11].
Вариации и обобщения[править | править код]
- См. также: Пополнение Дедекинда — Макнейла
Дедекиндовы сечения можно аналогично определить не только для рациональных чисел, но и в любом другом линейно упорядоченном множестве. См. Полнота (теория порядка). Можно показать, что применение этой процедуры к множеству вещественных чисел даёт снова
Аналог дедекиндовых сечений используется для построения сюрреальных чисел[12].
См. также[править | править код]
Примечания[править | править код]
- ↑ Математическая энциклопедия, 1979.
- ↑ Richard Dedekind. Stetigkeit und irrationale Zahlen. Friedrich Vieweg und Sohn, Braunschweig 1872. (online).
- ↑ Рихард Дедекинд. Непрерывность и иррациональные числа = Stetigkeit und irrationale Zahlen / пер. с нем. С. О. Шатуновского. — 4. — Матезис, 1923. Архивировано 16 июля 2017 года.
- ↑ Начала Евклида. Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии И. Н. Веселовского и М. Я. Выгодского. М.-Л.: ГТТИ, 1949—1951. книги I—VI на www.math.ru Архивная копия от 6 октября 2015 на Wayback Machine или на mccme.ru Архивная копия от 11 августа 2011 на Wayback Machine; книги VII—X на www.math.ru Архивная копия от 6 октября 2015 на Wayback Machine или на mccme.ru Архивная копия от 18 сентября 2011 на Wayback Machine; книги XI—XIV на www.math.ru Архивная копия от 6 октября 2015 на Wayback Machine или на mccme.ru Архивная копия от 20 сентября 2011 на Wayback Machine
- ↑ Bertrand, Joseph. Traité d'Arithmétique. — 1849. — «Несоизмеримое число можно определить, всего лишь указав, как величина, которую оно выражает, может быть образована с помощью единицы. В дальнейшем мы предполагаем, что это определение состоит из указания, какие соизмеримые числа меньше или больше данного.». Архивная копия от 17 января 2021 на Wayback Machine Источник. Дата обращения: 11 октября 2020. Архивировано 17 января 2021 года.
- ↑ Фихтенгольц, 1966, с. 17—18.
- ↑ Фихтенгольц, 1966, с. 18, 36.
- ↑ Фихтенгольц, 1966, с. 19—21.
- ↑ Фихтенгольц, 1966, с. 22—24.
- ↑ Фихтенгольц, 1966, с. 28—31.
- ↑ Фихтенгольц, 1966, с. 31—34.
- ↑ См. лекцию Конвея, примерно с 0:16:30 по 0:19:30. Дата обращения: 11 октября 2020. Архивировано 9 ноября 2020 года.
Литература[править | править код]
- Кудрявцев Л. Д. Дедекиндово сечение // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1979. — Т. 2: Д — Коо. — С. 65. — 1104 стб. : ил. — 150 000 экз.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: Наука, 1966. — Т. I. — 680 с.





















