Задача о независимом множестве
Зада́ча о незави́симом мно́жестве относится к классу NP-полных задач в области теории графов. Эквивалентна задаче о клике.
Определения[править | править код]
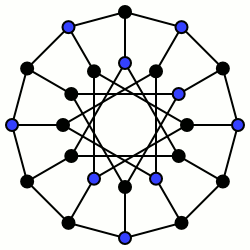
Множество вершин графа называется независимым, если никакие две вершины этого множества не соединены ребром. Другими словами, индуцированный этим множеством подграф состоит из изолированных вершин. Иногда также говорят, что каждое ребро графа инцидентно не более чем одной вершине из независимого множества. Задача распознавания (проблема разрешимости) выглядит так: существует ли в заданном графе G независимое множество размера k? Соответствующая ей оптимизационная задача, она же задача о независимом множестве, формулируется следующим образом: в заданном графе G требуется найти независимое множество максимального размера. Этот размер называют числом независимости, числом внутренней плотности или неплотностью и обозначают как [1][2].
Иногда эту задачу называют поиском наибольшего независимого множества. Не стоит путать это понятие с максимальным независимым множеством, или максимальным по включению независимым множеством, которое определяется как такое независимое множество вершин, что при добавлении к нему ещё одной (любой) вершины исходного графа оно перестаёт быть независимым (вообще говоря, таких множеств может быть несколько и разных размеров). Максимальное по включению независимое множество отнюдь не всегда является наибольшим. В то же время каждое наибольшее независимое множество по определению является также и максимальным по включению. Для нахождения (какого-то) максимального по включению независимого множества можно воспользоваться жадным алгоритмом, работающим за полиномиальное время, тогда как задача о наибольшем независимом множестве принадлежит к классу NP-полных задач.
Максимальное по включению независимое множество является доминирующим множеством. Любой граф содержит максимум 3n/3 максимальных по включению независимых множеств[3], однако бо́льшая часть графов имеет их куда меньше.
Число максимальных по включению независимых множеств в циклах из n вершин — это числа Перрина, а число максимальных по включению независимых множеств в путях с n вершинами задаётся последовательностью Падована[4]. Таким образом, оба числа пропорциональны степени 1,324718, пластическому числу.
Наименьшим независимым подмножеством в графе является любая вершина этого графа.
Связь с другими параметрами графов[править | править код]
Множество независимо тогда и только тогда, когда оно является кликой в дополнении графа, так что два понятия дополняют друг друга. Достаточно большие графы без больших клик имеют большие независимые множества, что является предметом исследования в теории Рамсея.
Множество независимо тогда и только тогда, когда его дополнение является вершинным покрытием. Сумма числа независимости и числа вершинного покрытия равна числу вершин графа (первое тождество Галлаи).
Раскраска вершин графа соответствует разбиению его вершин на независимые подмножества. Поэтому минимальное число красок, требующихся для раскраски вершин, хроматическое число , не меньше частного от деления числа вершин и числа независимости .
В двудольных графах, не имеющих изолированных вершин, число вершин в наибольшем независимом множестве равно числу рёбер в наименьшем рёберном покрытии (следствие из теоремы Кёнига).
Поиск независимых множеств[править | править код]
В информатике изучается несколько вычислительных задач, связанных с независимыми множествами:
- В задаче о наибольшем независимом множестве входом служит неориентированный граф, а выходом — наибольшее независимое множество в этом графе. Если существует несколько таких множеств, достаточно найти одно.
- В задаче о независимом множестве максимального веса входом служит неориентированный граф с весами, заданными для вершин, а выходом — независимое множество с максимальным общим весом. Задача о максимальном по включению независимом множестве является частным случаем этой задачи с весами, равными единице.
- В задаче перечисления максимальных по включению независимых множеств входом служит неориентированный граф, а выходом — список всех максимальных по включению независимых множеств. Задачу о наибольшем независимом множестве можно решать как подзадачу данной задачи, поскольку наибольшее независимое множество является максимальным по включению и должно попасть в этот список.
- В задаче о наличии независимого множества заданного размера входом служит неориентированный граф и число k, а выходом — Да/Нет: Да, если граф содержит независимое множество размера k, и Нет в противном случае.
Первые три задачи важны в практических приложениях, последняя же важна для теории NP-полноты для задач, связанных с независимыми множествами.
Задача о независимом множестве и задача о клике являются двойственными: клика в G — это независимое множество в дополнении графа G и наоборот. Таким образом, многие вычислительные результаты могут быть приложены одинаково хорошо к обоим задачам. Например, результаты, связанные с задачей о клике, имеют следующие следствия:
- Задача о наличии является NP-полной, а это означает, что существование (ровно как и не существование) эффективного алгоритма её решения не доказано. Существует эффективные (аппроксимирующие[5]) эвристические алгоритмы поиска максимального по весу независимого множества вершин в графе, примером которых может служить алгоритм Русова В.С. и Захаровой Д.А. имеющий сложность O(n3).
- Задача о наибольшем независимом множестве NP-трудна и её, кроме того, трудно аппроксимировать.
Поиск наибольшего независимого множества[править | править код]
Эту задачу иногда называют «упаковкой вершин».
Задача нахождения наибольшего независимого множества и задача о наибольшей клике полиномиально эквивалентны — можно найти наибольшее независимое множество путём поиска максимальной клики в дополнении графа, так что многие авторы особенно не заботятся о разделении этих двух задач. Обе задачи NP-полны, так что вряд ли их можно решить за полиномиальное время. Тем не менее, задача о наибольшем независимом множестве может быть решена эффективнее, чем за время O(n2 2n), которое даёт полный перебор, проверяющий все подмножества вершин, являются ли они независимыми множествами. Алгоритм Робсона[6] решает задачу за время O(20.276n), используя экспоненциальное пространство. Если есть ограничение на размер (полиномиальность пространства), существует алгоритм решения за время O*(1.2127n)[7].
Вопреки близкой связи между наибольшей кликой и наибольшим независимым множеством в произвольном графе, задачи нахождения независимого множества и клики могут существенно отличаться, когда решаются на специальном классе графов. Например, для разреженных графов (графы, в которых в любом подграфе число рёбер не больше числа вершин, умноженного на некоторую константу) наибольшая клика имеет ограниченный размер и может быть найдена точно за линейное время[8]. Тем не менее, для тех же классов графов, или даже для случая более жёстких ограничений у класса графов с ограниченной степенью, поиск наибольшего независимого множества является MAXSNP-полной, что означает, что для некоторой константы c (зависящей от степени) NP-трудно найти приближённое решение, отличающееся на множитель c от оптимального[9]. Однако эффективные приближённые алгоритмы известны, но для них гарантированная эффективность хуже, чем этот порог. Например, жадный алгоритм создаёт максимальное по включению независимое множество, на каждом шаге выбирая вершину с минимальной степенью и удаляя её соседей. Этот алгоритм достигает гарантированной эффективности (Δ+2)/3 на графах с максимальной степенью Δ[10].
В некоторых классах графов (включая графы без клешней[11] и совершенные графы[12]; к последнему классу принадлежат и деревья) наибольшее независимое множество может быть найдено за полиномиальное время. Для планарных графов задача о наибольшем независимом множестве остаётся NP-полной для точного решения, но может быть аппроксимирована с любой гарантированной эффективностью c < 1 за полиномиальное время. Похожие приближённые схемы полиномиального времени существуют в любом семействе минорно замкнутых графов[13][14].
В двудольных графах все вершины, не входящие в наименьшее вершинное покрытие, могут быть включены в наибольшее независимое множество (смотри теорему Кёнига). Поэтому наибольшее независимое множество может быть найдено с помощью алгоритма нахождения наибольшего паросочетаний в двудольных графах.
Поиск максимальных по включению независимых множеств[править | править код]
Все максимальные по включению независимые множества можно найти за время O(3n/3).
Программное обеспечение для поиска независимых множеств[править | править код]
| Название | Лицензия | Язык API | Описание |
|---|---|---|---|
| igraph | GPL | C, Python, R, Ruby | точное решение |
| NetworkX | BSD | Python | приближённое решение, см. процедуру maximum_independent_set |
| OpenOpt | BSD | Python | точные и приближённые решения, возможность указать вершины, которые следует включить / исключить. См. класс STAB для деталей и примеров |
Наибольшее независимое множество в дереве[править | править код]
Если данный граф является деревом, то задача о независимом множестве эффективно решается методом динамического программирования.
Оптимальная подструктура задачи[править | править код]
Структура дерева сама подсказывает решение задачи. Именно, обозначим корнем дерева любую вершину и назовем её . Пусть обозначает размер наибольшего независимого множества вершин поддерева, корнем которого является вершина . Тогда ответом на задачу будет являться .
Нетрудно видеть, что если мы включаем вершину u в наибольшее независимое множество, то его мощность увеличивается на 1, но его детей мы брать не можем (так как они соединены ребром с вершиной u); если же мы не включаем эту вершину, то мощность наибольшего независимого множества будет равна сумме размеров независимых множеств детей этой вершины. Остается только выбрать максимум из этих двух вариантов, чтобы получить решение задачи:
где grandchild обозначает всякого «внука» вершины, а child обозначает всякого потомка вершины.
Псевдокод[править | править код]
Считаем, что в вершине u хранится :
function get_independent_set(Node u)
{
если I(u) уже посчитано, то возвратить I(u)
// мощность множества, которое можно получить, если не брать вершину u
children_sum = 0
// мощность множества, которое можно получить, если взять вершину u
grandchildren_sum = 0
// цикл по всем детям
for i := 1 to child_num do
children_sum = children_sum + get_independent_set(children[i])
// цикл по всем внукам
for i:= 1 to grandchildren_num
grandchildren_sum = grandchildren_sum + get_independent_set(grandchildren[i])
// запоминаем, чтобы не пересчитывать ещё раз
I(u) = max(1 + grandchildren_sum, children_sum)
возвратить I(u)
}
Вызов get_independent_set(r) даст ответ на задачу. Время выполнения алгоритма, очевидно, O(|V| + |E|).
См. также[править | править код]
- Алгоритм Брона — Кербоша для нахождения максимальных по включению независимых множеств вершин.
Примечания[править | править код]
- ↑ Chris Godsil, Gordon Royle. . Algebraic Graph Theory. — New York: Springer, 2001. — ISBN 0-387-95220-9. — P. 3.
- ↑ Евстигнеев В. А., Касьянов В. Н. . Словарь по графам в информатике. — Новосибирск, 200. — (Конструирование и оптимизация программ, вып. 17). — ISBN 978-591124-036-3.
- ↑ Moon J. W., Moser L. On cliques in graphs // Israel Journal of Mathematics. — 1965. — Vol. 3, no. 1. — P. 23–28. — doi:10.1007/BF02760024.
- ↑ Füredi, Zoltán. The number of maximal independent sets in connected graphs // Journal of Graph Theory. — 1987. — Vol. 11, no. 4. — P. 463–470. — doi:10.1002/jgt.3190110403.
- ↑ Из приведённой ниже статьи Русова и Захаровой: В последнее время наибольший интерес для решения подобного рода задач представляют эвристические алгоритмы, то есть алгоритмы, которые всё же позволяют решить NP-полную задачу, но с некоторой погрешностью. Основными критериями оценки эвристического алгоритма являются «эффективность по времени» и погрешность по отношению к точному алгоритму.
- ↑ Robson J. M. Algorithms for maximum independent sets // Journal of Algorithms. — 1986. — Vol. 7, no. 3. — P. 425–440. — doi:10.1016/0196-6774(86)90032-5.
- ↑ Nicolas Bourgeois, Bruno Escoffier, Vangelis Th. Paschos, Johan M. M. van Rooij. . A bottom-up method and fast algorithms for MAX INDEPENDENT SET // Algorithm theory—SWAT 2010. — Berlin: Springer, 2010. — (Lecture Notes in Computer Science, vol. 6139). — doi:10.1007/978-3-642-13731-0_7. — P. 62–73.
- ↑ Chiba N., Nishizeki T. Arboricity and subgraph listing algorithms // SIAM Journal on Computing. — 1985. — Vol. 14, no. 1. — P. 210–223. — doi:10.1137/0214017.
- ↑ Piotr Berman, Toshihiro Fujito. . On approximation properties of the Independent set problem for degree 3 graphs // Fourth International Workshop on Algorithms and Data Structures. — Springer, 1995. — (Lecture Notes in Computer Science, vol. 995). — doi:10.1007/3-540-60220-8_84. — P. 449–460.
- ↑ Halldórsson M. M., Radhakrishnan J. Greed is good: Approximating independent sets in sparse and bounded-degree graphs // Algorithmica. — 1997. — Vol. 18, no. 1. — P. 145–163. — doi:10.1007/BF02523693..
- ↑ Sbihi, 1980.
- ↑ Grötschel, Lovász, Schrijver, 1988.
- ↑ Brenda S. Baker. Approximation algorithms for NP-complete problems on planar graphs // Journal of the ACM. — 1994. — Vol. 41, no. 1. — P. 153–180. — doi:10.1145/174644.174650.
- ↑ Martin Grohe. Local tree-width, excluded minors, and approximation algorithms // Combinatorica. — 2003. — Vol. 23, no. 4. — P. 613–632. — doi:10.1007/s00493-003-0037-9.
Литература[править | править код]
- Chris Godsil, Gordon Royle. . Algebraic Graph Theory. — New York: Springer, 2004. — ISBN 0-387-95220-9.
- Grötschel M., Lovász L., Schrijver A. . 9.4. Coloring Perfect Graphs // Geometric Algorithms and Combinatorial Optimization. — Springer, 1988. — (Algorithms and Combinatorics, vol. 2). — ISBN 0-387-13624-X. — P. 296–298.
- Karp, Richard. Reducibility Among Combinatorial Problems // Proceedings of a Symposium on the Complexity of Computer Computations. — 1972.
- Michael R. Garey, David S. Johnson. . Computers and Intractability: A Guide to the Theory of NP-Completeness. — W. H. Freeman, 1979. — ISBN 0-7167-1045-5.
- Sanjoy Dasgupta, Christos H. Papadimitriou, Umesh Vazirani. . Chapter 6. Dynamic Programming // Algorithms. — McGraw-Hill Science/Engineering/Math, 2006. — ISBN 0073523402. — P. 336.
- Sbihi, Najiba Sbihi. Algorithme de recherche d'un stable de cardinalité maximum dans un graphe sans étoile // Discrete Mathematics. — 1980. — Vol. 29, no. 1. — P. 53–76. — doi:10.1016/0012-365X(90)90287-R.
Ссылки[править | править код]
- Weisstein, Eric W. Maximal Independent Vertex Set (англ.) на сайте Wolfram MathWorld.
- Challenging Benchmarks for Maximum Clique, Maximum Independent Set, Minimum Vertex Cover and Vertex Coloring
- Поликарпова Н., Герасименко А. Методы решения труднорешаемых задач
- Слайды лекции о динамическом программировании
- Видео лекции о динамическом программировании
- Русов В.С., Захарова Д.А. Эвристический алгоритм поиска максимального по весу независимого множества вершин в графе
Для улучшения этой статьи желательно:
|








