Парадокс Крамера: различия между версиями

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску
Интерактивная навигация по истории
[отпатрулированная версия][отпатрулированная версия]
← Предыдущая правкаСледующая правка →
Содержимое удалено Содержимое добавлено
ВизуальныйВики-текст
стилевые правки, уточнения, убрал шаблон
Строка 1: Строка 1:
[[Файл:Two cubic curves.png|thumb|Кубические кривые, пересекающиеся в 9 точках]]
[[Файл:Two cubic curves.png|thumb|Кубические кривые, пересекающиеся в 9 точках]]
'''Парадокс Крамера''' или '''парадокс Эйлера — Крамера'''<ref name=Weisstein>Weisstein, Eric W. "Cramér-Euler Paradox." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Cramer-EulerParadox.html</ref> — это утверждение, что число точек пересечения двух кривых высокого порядка на [[Плоскость|плоскости]] может быть выше числа произвольных точек, которые обычно нужны для однозначного определения каждой такой кривой. Парадокс назван именем математика из [[Женева (кантон)|Женевы]] [[Крамер, Габриэль|Габриэля Крамера]].
'''Парадокс Крамера''' или '''парадокс Эйлера — Крамера'''<ref name=Weisstein>Weisstein, Eric W. "Cramér-Euler Paradox." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Cramer-EulerParadox.html</ref> — это утверждение, что число точек пересечения двух кривых высокого порядка на [[Плоскость|плоскости]] может быть больше числа произвольных точек, которые обычно нужны для однозначного определения каждой такой кривой. Парадокс назван именем математика из [[Женева (кантон)|Женевы]] [[Крамер, Габриэль|Габриэля Крамера]].


Парадокс является результатом наивного понимания двух теорем:
Парадокс является результатом наивного понимания двух теорем:
Строка 12: Строка 12:


== История ==
== История ==
⚫
Парадокс первым опубликовал [[Маклорен, Колин|Маклорен]]{{sfn|Maclaurin|1720}}{{sfn|Tweedie|1891|с=87–150}}. Крамер и [[Эйлер, Леонард|Эйлер]] переписывались по поводу парадокса в 1744—1745 годах и Эйлер объяснил проблему Крамеру{{sfn|Struik|1969|с=182}}. Проблема стала называться ''парадоксом Крамера'' после публикации в 1750 году в книге Крамера ''Introduction à l'analyse des lignes courbes algébriques'', хотя Крамер и указал на Маклорена как источник утверждения{{sfn|Tweedie|1915|с=133–151}}. Примерно в то же самое время Эйлер опубликовал примеры, показывающие, что кубическая кривая может не определяться однозначно 9 точками{{sfn|Struik|1969|с=182}}{{sfn|Euler|1750|с=219-233}} и обсудил проблему в своей книге {{не переведено 5|Introductio in analysin infinitorum|||Introductio in analysin infinitorum}}. Результат был обнародован [[Стирлинг, Джеймс|Джеймсом Стирлингом]], а объяснение дал [[Плюккер, Юлиус|Юлиус Плюккер]]<ref name=Weisstein/>.

⚫
Парадокс первым опубликовал [[Маклорен, Колин|Маклорен]]{{sfn|Maclaurin|1720}}{{sfn|Tweedie|1891|с=87–150}}. Крамер и [[Эйлер, Леонард|Эйлер]] переписывались по поводу парадокса в письмах в 1744—1745 годах и Эйлер объяснил проблему Крамеру{{sfn|Struik|1969|с=182}}. Проблема стала называться ''парадоксом Крамера'' после публикации в 1750 в книге Крамера ''Introduction à l'analyse des lignes courbes algébriques'', хотя Крамер и указал на Маклорена как источник утверждения{{sfn|Tweedie|1915|с=133–151}}. Примерно в то же самое время Эйлер опубликовал примеры, показывающие кубическую кривую, которая не определяется однозначно 9 точками{{sfn|Struik|1969|с=182}}{{sfn|Euler|1750|с=219-233}} и обсудил проблему в своей книге {{не переведено 5|Introductio in analysin infinitorum|||Introductio in analysin infinitorum}}. Результат был обнародован [[Стирлинг, Джеймс|Джеймсом Стирлингом]], а объяснение дал [[Плюккер, Юлиус|Юлиус Плюккер]]<ref name=Weisstein/>.


==Никакого парадокса для прямых и невырожденных конических сечений ==
==Никакого парадокса для прямых и невырожденных конических сечений ==

Для кривых первого порядка (то есть [[Прямая|прямых]]) парадокс не проявляется, поскольку ''n'' = 1, так что ''n''<sup>2</sup> = 1 < ''n''(''n'' + 3) / 2 = 2. В общем случае две различные прямые ''L''<sub>1</sub> и ''L''<sub>2</sub> пересекаются в одной точке ''P'', если только прямые не имеют одинаковый наклон, и в этом случае прямые не пересекаются вообще. Одна точка недостаточна для однозначного определения прямой (нужны две). Через точку ''P'' проходят не две, а бесконечно много прямых.
Для кривых первого порядка (то есть [[Прямая|прямых]]) парадокс не проявляется, поскольку ''n'' = 1, так что ''n''<sup>2</sup> = 1 < ''n''(''n'' + 3) / 2 = 2. В общем случае две различные прямые ''L''<sub>1</sub> и ''L''<sub>2</sub> пересекаются в одной точке ''P'', если только прямые не имеют одинаковый наклон, и в этом случае прямые не пересекаются вообще. Одна точка недостаточна для однозначного определения прямой (нужны две). Через точку ''P'' проходят не две, а бесконечно много прямых.


Аналогично два невырожденных конических сечения пересекаются максимум в 4 конечных точках, а для однозначного определения невырожденной кривой нужно 5 точек.
Аналогично, два невырожденных конических сечения пересекаются максимум в 4 конечных точках, а для однозначного определения невырожденной кривой нужно 5 точек.


== Пример Крамера для кубических кривых ==
== Пример Крамера для кубических кривых ==
В письме Эйлеру Крамер указал, что кубические кривые <math>x^3 - x = 0</math> and <math>y^3 - y = 0</math> пересекаются ровно в 9 точках (каждое уравнение представляет набор трёх параллельных прямых <math>x = -1, x = 0, x = +1</math> и <math>y = -1, y = 0, y = +1</math> соответственно). Получается, что эти 9 точек не достаточны для однозначного определения кубической кривой, так что, по меньшей мере в вырожденном случае, утверждение имеет место.
В письме Эйлеру Крамер указал, что кубические кривые <math>x^3 - x = 0</math> и <math>y^3 - y = 0</math> пересекаются ровно в 9 точках (каждое уравнение представляет набор трёх параллельных прямых <math>x = -1, x = 0, x = +1</math> и <math>y = -1, y = 0, y = +1</math> соответственно). Получается, что эти 9 точек не достаточны для однозначного определения кубической кривой, так что, по меньшей мере в вырожденном случае, утверждение имеет место.


==Примечания==
==Примечания==
Строка 83: Строка 81:
[[Категория:Математические парадоксы]]
[[Категория:Математические парадоксы]]
[[Категория:Алгебраические кривые]]
[[Категория:Алгебраические кривые]]
{{rq|checktranslate|style}}

Версия от 07:52, 7 марта 2018

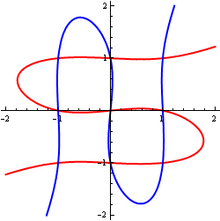
Кубические кривые, пересекающиеся в 9 точках

Парадокс Крамера или парадокс Эйлера — Крамера[1] — это утверждение, что число точек пересечения двух кривых высокого порядка на плоскости может быть больше числа произвольных точек, которые обычно нужны для однозначного определения каждой такой кривой. Парадокс назван именем математика из Женевы Габриэля Крамера.

Парадокс является результатом наивного понимания двух теорем:

Заметим, что для всех , так что наивно кажется, что для степеней три и выше могло бы быть достаточно точек пересечения двух кривых, чтобы они однозначно определяли обе кривые.

Проблема заключается в том, что в некоторых вырожденных случаях n(n + 3) / 2 точек оказывается недостаточно для однозначного определения кривой.

История

Парадокс первым опубликовал Маклорен[2][3]. Крамер и Эйлер переписывались по поводу парадокса в 1744—1745 годах и Эйлер объяснил проблему Крамеру[4]. Проблема стала называться парадоксом Крамера после публикации в 1750 году в книге Крамера Introduction à l'analyse des lignes courbes algébriques, хотя Крамер и указал на Маклорена как источник утверждения[5]. Примерно в то же самое время Эйлер опубликовал примеры, показывающие, что кубическая кривая может не определяться однозначно 9 точками[4][6] и обсудил проблему в своей книге Introductio in analysin infinitorum[en]. Результат был обнародован Джеймсом Стирлингом, а объяснение дал Юлиус Плюккер[1].

Никакого парадокса для прямых и невырожденных конических сечений

Для кривых первого порядка (то есть прямых) парадокс не проявляется, поскольку n = 1, так что n2 = 1 < n(n + 3) / 2 = 2. В общем случае две различные прямые L1 и L2 пересекаются в одной точке P, если только прямые не имеют одинаковый наклон, и в этом случае прямые не пересекаются вообще. Одна точка недостаточна для однозначного определения прямой (нужны две). Через точку P проходят не две, а бесконечно много прямых.

Аналогично, два невырожденных конических сечения пересекаются максимум в 4 конечных точках, а для однозначного определения невырожденной кривой нужно 5 точек.

Пример Крамера для кубических кривых

В письме Эйлеру Крамер указал, что кубические кривые и пересекаются ровно в 9 точках (каждое уравнение представляет набор трёх параллельных прямых и соответственно). Получается, что эти 9 точек не достаточны для однозначного определения кубической кривой, так что, по меньшей мере в вырожденном случае, утверждение имеет место.

Примечания

  1. ↑ 1 2 Weisstein, Eric W. "Cramér-Euler Paradox." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Cramer-EulerParadox.html
  2. ↑ Maclaurin, 1720.
  3. ↑ Tweedie, 1891, с. 87–150.
  4. ↑ 1 2 Struik, 1969, с. 182.
  5. ↑ Tweedie, 1915, с. 133–151.
  6. ↑ Euler, 1750, с. 219-233.

Литература

  • Colin Maclaurin. Geometria Organica. — London, 1720.
  • Charles Tweedie. V.—The "Geometria Organica" of Colin Maclaurin: A Historical and Critical Survey // Transactions of the Royal Society of Edinburgh. — 1891. — Январь (т. 36, вып. 1-2). — doi:10.1017/S0080456800004932.
  • Charles Tweedie. A Study of the Life and Writings of Colin Maclaurin // The Mathematical Gazette. — 1915. — Т. 8, вып. 119. — JSTOR 3604693.
  • Struik D. J. A Source Book in Mathematics, 1200-1800. — 1969. — ISBN 0674823559.
  • Euler L. Sur une contradiction apparente dans la doctrine des lignes courbes. // Mémoires de l'Académie des Sciences de Berlin. — 1750. — Т. 4.

Ссылки

Источник — https://ru.wikipedia.org/w/index.php?title=Парадокс_Крамера&oldid=91367452