Код Грея
| Число | Бинарный код | Код Грея |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
Код Гре́я — двоичный код, иначе зеркальный код, он же код с отражением, в котором две «соседние» (в упорядоченном, то есть лексикографическом, наборе) кодовые комбинации различаются только цифрой в одном двоичном разряде. Иными словами, расстояние Хэмминга между соседними кодовыми комбинациями равно 1.
Наиболее часто на практике применяется рефлексивный двоичный код Грея, хотя в общем случае существует бесконечное множество кодов Грея со значениями цифр в разрядах, взятых из различных алфавитов. В большинстве случаев, под термином «код Грея» понимают именно рефлексивный бинарный код Грея.
Изначально предназначался для защиты от ложного срабатывания электромеханических переключателей. Сегодня коды Грея широко используются для упрощения выявления и исправления ошибок в системах связи, а также в формировании сигналов обратной связи в системах управления.
Название[править | править код]
Код Грея назван «рефлексивным» (отражённым) из-за того, что первая половина значений при изменении порядка эквивалентна второй половине, за исключением старшего бита. Старший бит просто инвертируется. При делении каждой новой половины пополам это свойство сохраняется (см. самоподобие).
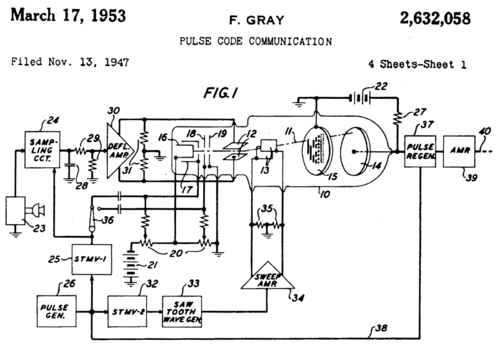
Код назван в честь исследователя Фрэнка Грея, работавшего в лаборатории «Bell labs». Грей запатентовал (патент № 2632058) и впервые использовал этот код в своей импульсной системе связи.
Применения[править | править код]
Код Грея используется в передаче меняющихся цифровых сигналов в отсутствие тактового сигнала синхронизации (например, во многих видах датчиков). Представим себе, что код (обычный двоичный) перескакивает 3→4, или 0112 → 1002. Если из-за несовершенства считывателя мы прочитаем первый бит от 011, а остальные два — от 100, мы получим 0002=0 — число, далёкое от реальных значений. В коде Грея никаких посторонних значений не будет: перескок будет в одном разряде, 010G → 110G, и мы считаем либо старое 010G=3, либо новое 110G=4.
Если считыватель настолько медленный, что за время считывания показания несколько раз сменились, код Грея гарантирует, что ошибка будет невелика — меньше, чем реальное изменение сигнала. Например, если за время считывания показания сменились 010G=3 → 110G → 111G=5, то помимо этих трёх значений, можно получить 011G=2 — выходит ошибка на единицу.
Если датчик круговой (например, угловой энкодер), то ему приходится перескакивать и с максимума до нуля. Такой перескок (с 100G=7 до 000G=0) тоже изменяет один разряд.

Коды Грея часто используются в датчиках-энкодерах. Их использование удобно тем, что два соседних значения шкалы сигнала отличаются только в одном разряде. Также они используются для кодирования номера дорожек в жёстких дисках.
Код Грея можно использовать также и для решения задачи о Ханойских башнях.
Широко применяются коды Грея и в теории генетических алгоритмов для кодирования генетических признаков, представленных целыми числами.
Код Грея используется для генерации сочетаний методом двери-вертушки[1].
В некоторых компьютерных играх (например, Duke Nukem 3D) для успешного прохождения уровня требуется подобрать нужную комбинацию положений нескольких переключателей. Никаких подсказок нет, надо просто перебрать все комбинации. Для минимизации числа переключений при переборе вариантов следует использовать код Грея. Например, если переключателей три, пробуем их в порядке 000, 001, 011, 010, 110…
Сложные датчики, требующие синхросигнала, отходят от кода Грея и работают в обычном двоичном[2].
Алгоритмы преобразования[править | править код]
Преобразование двоичного кода в код Грея[править | править код]
Коды Грея легко получаются из двоичных чисел путём побитовой операции «Исключающее ИЛИ» с тем же числом, сдвинутым вправо на один бит и в котором старший разряд заполняется нулём. Следовательно, i-й бит кода Грея Gi выражается через биты двоичного кода Bi следующим образом:
где — операция «исключающее ИЛИ»; биты нумеруются справа налево, начиная с младшего.
Ниже приведён алгоритм преобразования из двоичной системы счисления в код Грея, записанный на языке C:
unsigned int grayencode(unsigned int g)
{
return g ^ (g >> 1);
}
Однако, необходимо помнить, что данный алгоритм будет работать правильно, если компилятор реализует нециклический логический сдвиг (например, стандарт языка C не уточняет тип сдвига для знаковых чисел, но для unsigned типов поддержка гарантируется).
Тот же самый алгоритм, записанный на языке Паскаль:
function BinToGray(b: integer): integer;
begin
BinToGray := b xor (b shr 1)
end;
Пример: преобразовать двоичное число 10110 в код Грея.
10110 01011 ----- XOR 11101
Преобразование кода Грея в двоичный код[править | править код]
Обратный алгоритм — преобразование кода Грея в двоичный код — можно выразить рекуррентной формулой
причём преобразование осуществляется побитно, начиная со старших разрядов, и значение , используемое в формуле, вычисляется на предыдущем шаге алгоритма. Действительно, если подставить в эту формулу вышеприведённое выражение для i-го бита кода Грея, получим
Однако приведённый алгоритм, связанный с манипуляцией отдельными битами, неудобен для программной реализации, поэтому на практике используют видоизменённый алгоритм:
где N — число битов в коде Грея (для увеличения быстродействия алгоритма в качестве N можно взять номер старшего ненулевого бита кода Грея); знак означает суммирование при помощи операции «исключающее ИЛИ», то есть
Действительно, подставив в формулу выражение для i-го бита кода Грея, получим
Здесь предполагается, что бит, выходящий за рамки разрядной сетки (), равен нулю.
Ниже приведена функция на языке С, реализующая данный алгоритм. Она осуществляет последовательный сдвиг вправо и суммирование исходного двоичного числа, до тех пор, пока очередной сдвиг не обнулит слагаемое.
unsigned int graydecode(unsigned int gray)
{
unsigned int bin;
for (bin = 0; gray; gray >>= 1) {
bin ^= gray;
}
return bin;
}
Тот же самый алгоритм, записанный на языке Паскаль:
function GrayToBin(b: integer): integer;
var g: integer;
begin
g := 0;
while b > 0 do begin
g := g xor b;
b := b shr 1;
end;
GrayToBin := g;
end;
Пример: преобразовать код Грея 11101 в двоичный код.
11101 01110 00111 00011 00001 ----- 10110
Быстрое преобразование 8/16/24/32-разрядного значения кода Грея в двоичный код на языке C (Примечание: исходный код Грея является составным. Где каждая тетрада бит является отдельным числом и закодирована отдельно. Этот код не является полноценным кодом Грея. И правило изменения одного бита при переходе к новому числу сохраняется только в пределах каждой четвёрки. Например при переходе от 0x0F к 0x10 изменяются одновременно два бита так как мы имеем изменение двух тетрад 0->1 и F->0):
int gray2bin(int x)
{
return x ^ ((x & 0x88888888) >> 3) ^ ((x & 0xCCCCCCCC) >> 2) ^ ((x & 0xEEEEEEEE) >> 1);
}
Простой способ преобразования двоичного числа в код Грея выполняется по правилу: старший разряд записывается без изменения, каждый следующий символ кода Грея нужно инвертировать, если в натуральном коде перед этим была получена «1», и оставить без изменения, если в натуральном коде был получен «0».
Генерация кодов Грея[править | править код]
Код Грея для n бит может быть рекурсивно построен на основе кода для n-1 бит путём переворачивания списка бит (то есть записыванием кодов в обратном порядке), конкатенации исходного и перевёрнутого списков, дописывания нулей в начало каждого кода в исходном списке и единиц — в начало кодов в перевёрнутом списке. Так, для генерации списка для n = 3 бит на основании кодов для двух бит необходимо выполнить следующие шаги:
| Коды для n = 2 бит: | 00, 01, 11, 10 | |
| Перевёрнутый список кодов: | 10, 11, 01, 00 | |
| Объединённый список: | 00, 01, 11, 10 | 10, 11, 01, 00 |
| К начальному списку дописаны нули: | 000, 001, 011, 010 | 10, 11, 01, 00 |
| К перевёрнутому списку дописаны единицы: | 000, 001, 011, 010 | 110, 111, 101, 100 |
Ниже представлен один из алгоритмов создания последовательности кода Грея заданной глубины, записанный на языке Perl:
my $depth = 16; # generate 16 Gray codes, 4 bits wide each
my @gray_codes = ( '0', '1' );
while(scalar(@gray_codes)<$depth)
{
my @forward_half=map{'0'.$_} @gray_codes;
my @reverse_half=map{'1'.$_} reverse(@gray_codes);
@gray_codes=(@forward_half,@reverse_half);
}
Рекурсивная функция построения кода Грея на языке C:
//n -- требуемая длина кода,
//m -- указатель на массив, способный хранить
// все коды Грея, длиной до n
// (должен быть выделен до вызова функции)
//depth -- параметр рекурсии
int gray (int n, int* m, int depth)
{
int i, t = (1 << (depth - 1));
if (depth == 0)
m[0] = 0;
else {
//массив хранит десятичные записи двоичных слов
for (i = 0; i < t; i++)
m[t + i] = m[t - i - 1] + (1 << (depth - 1));
}
if (depth != n)
gray(n, m, depth + 1);
return 0;
}
Быстрое преобразование 8/16/24/32-разрядного двоичного кода в код Грея на языке C. (Примечание: полученный код не является полноценным кодом Грея. Данный код преобразовывает в код Грея каждые 4 бита отдельно, рассматривая их как отдельные числа. В результате полученный код состоит из множества 4 битных кодов грея. И правило изменения одного бита при переходе к новому числу сохраняется только в пределах каждой четвёрки. Например при переходе от 0x0F к 0x10 изменяются одновременно два бита так как мы имеем изменение двух тетрад 0->1 и F->0):
int bin2gray(int x)
{
return x ^ ((x & 0xEEEEEEEE) >> 1);
}
Необычные вариации кода Грея[править | править код]
Сбалансированный код Грея[править | править код]
Если датчики имеют ограниченный ресурс по количеству переключений, хотелось бы, чтобы они изнашивались равномерно. В сбалансированном коде Грея в разных разрядах количество переключений настолько близко, насколько можно.
0 1 1 1 1 1 1 0 0 0 0 0 0 1 1 0 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 1 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 1 1 1 1
Здесь в 4-битном коде каждый разряд переключается четырежды. В 5-битном коде такое невозможно, приходится переключать один бит 8 раз, остальные — по 6.
Однодорожечный код Грея[править | править код]
Код Грея является однодорожечным, если все столбцы матрицы являются кольцевыми сдвигами друг друга. Это позволяет сделать угловой датчик с одной дорожкой.
Двухбитный код Грея является однодорожечным, это можно увидеть в компьютерной мыши — как в шариковом механизме старых мышей, так и в колесе прокрутки новых. Два датчика стоят в разных точках одной дорожки. Если довести эту систему до крайности — половина диска «чёрная», половина «белая», и датчики стоят на 90° друг относительно друга — то можно узнать абсолютное положение диска с дискретностью в 90°.
Для кодов Грея более высокой разрядности это не так, приходится увеличивать количество дорожек, это делает датчик громоздким и дорогим. Поэтому, если возможно, обходятся двумя дорожками — одна для двухбитного кода Грея, и одна — позиция нуля. Однако существуют коды, где дорожка именно одна, правда, все 2n позиций так закодировать невозможно. Для 5 бит рекорд — 30 позиций, для 9 — 360.
Двухмерный код Грея[править | править код]
Используется в квадратурной модуляции сигналов. Соседние точки «созвездия» отличаются одним битом, диагональные — двумя.
См. также[править | править код]
Примечания[править | править код]
- ↑ Кнут, Дональд Э. 1 // Искусство программирования, том 4А. Комбинаторные алгоритмы / генерация всех сочетаний (раздел 7.2.1.3). — М.: ООО «И. Д. Вильямс», 2016. — Т. 4. — С. 416. — 960 с. — ISBN 978-5-8459-1980-9.
- ↑ Спецификация магнитного энкодера Megatron MAB-25. Архивная копия от 13 июля 2015 на Wayback Machine (англ.)
Литература[править | править код]
- Black, Paul E. Gray code. 25 февраля 2004. NIST. [1] (англ.)









