Концентрация напряжений

Концентрация напряжений — явление возникновения повышенных местных напряжений в областях резких изменений формы упругого тела, а также в зонах контакта деталей. Область пространства, в которой возникают эти напряжения, называется концентратором напряжений.

Исследование концентрации напряжений

Концентрация напряжений характеризуется теоретическим коэффициентом концентрации напряжений — отношением максимального напряжения $\sigma$ в области концентратора к номинальному напряжению $\sigma _{n}$ (вычисленному в предположении отсутствия концентратора):

$k={\frac {\sigma }{\sigma _{n}}}$

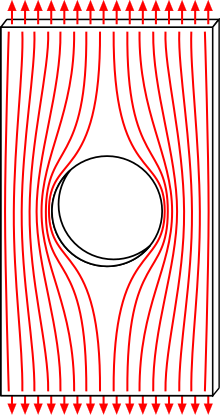
Классическим примером на концентрацию напряжений является задача Кирша о равномерном растяжении широкой полосы с малым отверстием посередине. Аналитический расчет показывает, что коэффициент концентрации напряжений в данном случае равен 3.

Концентрация напряжений в задаче Кирша, изображаемая с помощью силовых линий. Напряжение пропорционально густоте силовых линий

Определение коэффициента может производиться аналитическими, численными методами (например, методом конечных элементов), экспериментально (с помощью методов фотоупругости, хрупких покрытий). В современных конечно-элементных комплексах (ANSYS, Nastran, Abaqus, SolidWorks Simulation) исследование концентраторов напряжений может быть произведено с помощью сгущения конечно-элементной сетки или же специальных методов (субмоделирования, создания суперэлементов из частей конструкции, не подверженных концентрации напряжений).

Теоретический коэффициент описывает лишь влияние геометрии детали и способа нагружения на теоретическое напряжение, но не учитывает чувствительность самого материала к концентрации. Данная величина может неадекватно описывать снижение прочности при наличии концентратора. На практике при расчетах на усталость вводится понятие эффективного коэффициента концентрации напряжений — отношения пределов выносливости детали без концентратора $\sigma _{-1}$ и с концентратором $\sigma _{-1k}$:

$K_{\sigma D}={\frac {\sigma _{-1}}{\sigma _{-1k}}}$

С учётом различных факторов, влияющих на усталостную прочность, коэффициент вычисляется следующим образом:

$K_{\sigma D}={\frac {{\frac {K_{\sigma }}{K_{d\sigma }}}+{\frac {1}{K_{F\sigma }}}-1}{K_{V}}}$

где

• $K_{\sigma }$ — эффективный коэффициент концентрации напряжений, учитывающий влияние макроскопических концентраторов;
• $K_{d\sigma }$ — масштабный фактор (учитывает влияние размера детали);
• $K_{F\sigma }$ — коэффициент влияния качества поверхности;
• $K_{V}$ — коэффициент влияния поверхностного упрочнения.

Влияние на прочность конструкций

Концентрация напряжений может влиять на прочность по-разному в зависимости от характера нагружения:

• Статическое нагружение — влияние местных напряжений на прочность невелико. Возникновение напряжений, существенно превышающих предел текучести или даже предел прочности, может привести к местной текучести материала, но условий для её распространения и роста трещины не создаётся. Эти положения обобщены в одном из ключевых принципов механики деформируемого твердого тела — принципе Сен-Венана.
• Циклическое нагружение — концентрация напряжений является одним из основных факторов, приводящих к снижению прочности. В зонах концентрации напряжений создаются наиболее благоприятные условия для роста трещин.

Для борьбы с негативным влиянием концентрации напряжений применяются следующие методы:

• Изменение конструкции (разгружающие надрезы, скругления).
• Поверхностное упрочнение материала в зоне концентрации. Применяется термическая обработка (закалка токами высокой частоты, азотирование), обработка давлением (накатка роликом, дробеструйный наклёп).
• Точная обработка поверхности с целью уменьшения концентрации напряжений в микронеровностях (шлифование, обтачивание).

Концентрация напряжений стала причиной массовых катастроф первого в мире коммерческого реактивного авиалайнера «Комета». Иллюминаторы этого самолета имели квадратную форму, способствующую концентрации напряжений в углах, а заклепки, крепящие их, были установлены слишком часто, что способствовало быстрому распространению трещин.

Примеры концентраторов напряжений в технике

• Проточки (например, резьбовые)
• Острые углы
• Соединения с натягом
• Шпоночные пазы
• Переходы между участками с разным диаметром на валах
• Отверстия
• Сварные швы
• Дефекты поверхности

См. также

• Усталостное разрушение
• Принцип Сен-Венана

Литература

• Феодосьев В. И. Сопротивление материалов. — М.: Изд-во МГТУ им. Н. Э. Баумана, 1999. — 592 с. — (Механика в техническом университете).

Ссылки

• Савин Г. Н., Савченко В. И. Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
• Концентрация напряжений — статья из Большой советской энциклопедии. 
• Mike Busch. When Metal Lets Us Down (англ.) // CESSNA PILOTS ASSOCIATION Magazine. — 1999.
• EBI — Medical Glossary (недоступная ссылка) (недоступная ссылка с 27-05-2014 [3608 дней])
• Igor Kokcharov. Structural Integrity Analysis (англ.).