Спонтанное излучение
Спонтанное излучение, или спонтанное испускание, — процесс самопроизвольного испускания электромагнитного излучения квантовыми системами (атомами, молекулами) при их переходе из возбуждённого состояния в стабильное.
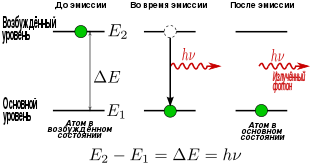
Феноменологическое определение Альберта Эйнштейна[править | править код]
Частота спонтанного электромагнитного излучения определяется разностью энергий i-го и k-го уровней системы:
Если населённость уровня с энергией равна , то мощность спонтанного излучения равна:
где — вероятность перехода с i-го уровня на k-й.
Полная вероятность спонтанного излучения:
Скорость спонтанной релаксации постоянна?[править | править код]
Феноменологически введённая Эйнштейном скорость спонтанной релаксации долгое время считалась внутренним неотъемлемым свойством атомов (молекул). При термодинамическом равновесии с окружением одним из важнейших признаков этого свойства является его необратимость. Эта особенность обусловлена взаимодействием атома (молекулы) с бесконечным числом мод вакуумного состояния. Изменение числа мод приводит к изменению скорости спонтанной релаксации. Чтобы этого добиться, можно поместить атом в резонатор[1].
Рассмотрим одноэлектронный атом, у которого два энергетических уровня и , разделенных между собой на величину . Среднее квадратичное амплитуды электрического вакуумного поля равно , где — восприимчивость среды, — объём пространства, в котором распространяется излучение. Энергия, которая излучается в одну моду, равна , здесь — матричный элемент электрического диполя. Эту частоту называют вакуумной Раби частотой.
Вероятность излучения фотона, известная как — коэффициент Эйнштейна, равна
здесь число мод в единичном частотном интервале (плотность мод).
Вероятность найти атом в возбужденном состоянии в момент времени после его возбуждения на уровень равна .
Причина спонтанного излучения[править | править код]
Процесс спонтанного излучения невозможно объяснить с позиций первоначальной версии квантовой механики, где имело место квантование уровней энергии атома, но не было квантования электромагнитного поля. Возбуждённые состояния атомов представляют собой точные стационарные решения уравнения Шредингера. Таким образом, атомы должны оставаться неограниченно долго в возбужденном состоянии. Причиной спонтанного излучения является взаимодействие атома с нулевыми колебаниями электромагнитного поля в вакууме. Состояния атома перестают быть стационарными в результате воздействия составляющей нулевых колебаний с частотой, равной частоте испускаемого кванта[2].
См. также[править | править код]
Примечания[править | править код]
- ↑ Serge, KLleppner, 1989.
- ↑ А. Б. Мигдал, В. П. Крайнов. Глава 1. Размерные и модельные оценки. 4. Оценки в квантовой электродинамике. Нулевые колебания электромагнитного поля // Приближенные методы квантовой механики. — Москва: Наука, 1966. — С. 47—50.
Литература[править | править код]
- Спонтанное испускание — статья из Физической энциклопедии
- Serge Haroche and Daniel KLleppner. Cavity Quantum Electrodynamics. — Physics Today, 1989. — С. 24.












![{\displaystyle [\hbar \omega /{2}\varepsilon _{0}V]^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/979bb258baf3fe473aba380a608d506e503df15e)









