Формула Маннинга
Перейти к навигации
Перейти к поиску
Уравнение Маннинга (или уравнение Гоклера — Маннинга) — эмпирическая зависимость скорости безнапорного потока в открытом русле от формы и размеров поперечного сечения и шероховатости стенок.
где:
- — средняя скорость (м/с);
- — коэффициент шероховатости;
- — гидравлический радиус (м);
- — гидравлический уклон (м/м).
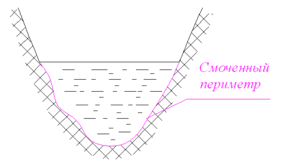
Гидравлический радиус вычисляется по формуле:
где:
- — площадь поперечного сечения (м²);
- — смоченный периметр (м).
Впервые на зависимость между и указал французский инженер П. Ж. Гоклер в 1868. Эту зависимость затем уточняли другие исследователи, в том числе ирландский инженер Р. Маннинг, в честь которого оказалась названа формула. В 2002 г. формула Маннинга, до того бывшая чисто эмпирической, была выведена теоретически аргентинцами Г. Джоя и Ф. А. Бомбарделли.
Литература[править | править код]
- Gauckler P. G. Du movement de l’eau dans les conduits//Annales des Ponts et Chaussées, 1868, 15, р. 229—281.
- Gioia, G., Bombardelli F. A. Scaling and similarity in open channel flows. Physical Review Letters, 88(1), 2002. (https://web.archive.org/web/20080625034622/http://www.mechse.uiuc.edu/research/gioia/Art/manning.pdf)
- Manning R. On the flow of water in open channels and pipes // Proceedings of the Institution of Civil Engineers of Ireland, 1890, 20, р. 161—206.
См. также[править | править код]
- Формула Куттера
- Формула Шези








