Четырёхполюсник
Четырёхпо́люсник — электрическая цепь, разновидность многополюсника, имеющая четыре точки подключения[1]. Как правило, две точки являются входом, две другие — выходом.
Общие сведения[править | править код]
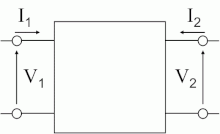
При анализе электрических цепей очень часто бывает удобным выделить фрагмент цепи, имеющий две пары зажимов. Поскольку электрические (электронные) цепи очень часто связаны с передачей энергии или обработкой и преобразованием информации, одну пару зажимов обычно называют «входными», а вторую — «выходными». На входные зажимы подаётся исходный сигнал, с выходных снимается преобразованный.
Такими четырёхполюсниками являются, например, трансформаторы, усилители, фильтры, стабилизаторы напряжения, телефонные линии, линии электропередачи и т. д.
Однако математическая теория четырёхполюсников не предполагает никаких предопределённых потоков энергии/информации в цепях, поэтому названия «входные» и «выходные» являются данью традиции и с этой оговоркой будут использоваться далее.
Состояния входных и выходных зажимов определяются четырьмя параметрами: напряжением и током во входной (U1, I1) и выходной (U2, I2) цепях. В этой системе параметров линейный четырёхполюсник описывается системой из двух линейных уравнений, причём два из четырёх параметров состояния являются исходными, а два других — определяемыми. Для нелинейных четырёхполюсников зависимость может носить более сложный характер. Например, выходные параметры через входные можно выразить системой
В дальнейшем будет использоваться запись системы уравнений в матричном виде, как наиболее удобная для восприятия.
Системы параметров[править | править код]
Линейный четырёхполюсник, не содержащий независимых источников (напряжения и/или тока), описывается четырьмя параметрами — два напряжения и два тока. Любые две величины из четырёх можно определить через оставшиеся две. Поскольку число сочетаний 2 из 4 — 6, используется одна из шести систем записи формальных параметров четырёхполюсника[2]:
- A-форма U1=AU2+BI2; I1=CU2+DI2, где A, B, C, D — A-параметры, обобщенные[3] или комплексные[4] параметры.
- Y-форма I1=Y11U1+Y12U2; I2=Y21U1+Y22U2, где Y11, Y12, Y21, Y22 — Y-параметры, или параметры проводимостей[5].
- Z-форма U1=Z11I1+Z12I2; U2=Z21I1+Z22I2, где Z11, Z12, Z21, Z22 — Z-параметры, или параметры сопротивлений[5].
- H-форма U1=h11I1+h12U2; I2=h21I1+h22U2, где h11, h12, h21, h22 — h-параметры, которые применяются при рассмотрении схем с транзисторами[3].
- G-форма I1=G11U1+G12I2; U2=G21U1+G22I2, где G — это параметр который используется при рассмотрении ламповых схем.
- B-форма U2=B11U1+B12I1; I2=B21U1+B22I1
Конкретная система выбирается из соображений удобства. Выбор зависит от того, какой параметр (напряжение или ток) является входным и какой — выходным сигналом для данного четырёхполюсника.
В указанных системах формальных параметров не могут быть учтены произвольные внутренние источники (например, постоянного тока), допускаются только управляемые генераторы тока и управляемые генераторы напряжения, которые управляются входными сигналами четырёхполюсника. Поэтому в качестве четырёхполюсников рассматриваются, как правило, эквивалентные схемы по переменному току.
Системы уравнений и эквивалентные схемы четырёхполюсников при использовании каждого типа параметров показаны в таблице.
Системы уравнений, эквивалентные схемы, измерение параметров[править | править код]
| Тип | Система уравнений | Эквивалентная схема | Измерение параметров |
|---|---|---|---|
 |
| ||
 |
| ||
 |
| ||
 |
| ||
|
| |||
|
|
Преобразование параметров[править | править код]
В качестве примера преобразуем h-параметры четырёхполюсника в y-параметры. Для этого нужно осуществить следующее преобразование системы уравнений:
Из первого уравнения исходной системы выразим I1:
Первое уравнение подставим во второе:
Преобразуем второе уравнение:
где
Получаем систему уравнений
Сравнивая её с целевой системой, получаем выражения для коэффициентов:
Определитель новой системы находим простой подстановкой:
|
|
|
|
| |||
|
|
|
|
| |||
|
|
|
|
| |||
|
|
|
|
|
|||
|
|
|
|
|
Преобразования схем[править | править код]
Rin, Rout — входное и выходное сопротивления; KI, KU — коэффициенты усиления по току и напряжению.
| Схема | ||||
|---|---|---|---|---|

|
|
|
|
|
В качестве примера найдем входное/выходное сопротивление и коэффициенты усиления по току и напряжению для четырёхполюсника, описанного h-параметрами.
- Входное сопротивление
Ненагруженный четырёхполюсник описывается системой
При подключении нагрузки
Преобразуем систему уравнений
Разновидности четырёхполюсников[править | править код]
Симметричный четырёхполюсник — четырёхполюсник, у которого схема одинакова относительно его входных и выходных зажимов. Тогда для симметричного четырёхполюсника Z11 = Z22. Ещё: если при перемене местами источника и приемника энергии их токи не меняются, то такой четырёхполюсник называется симметричным.
Пассивный четырёхполюсник — это четырёхполюсник, который не содержит источников энергии, либо содержит скомпенсированные источники энергии.
Активный четырёхполюсник — это четырёхполюсник, который содержит нескомпенсированные источники энергии.
Обратимый четырёхполюсник — четырёхполюсник, у которого выполняется теорема обратимости, то есть передаточное сопротивление входных и выходных контуров не зависит от того, какая пара зажимов входная, а какая выходная: U1/I2=U2/I1
Частные случаи четырёхполюсников[править | править код]
Идеальный трансформатор[править | править код]
Идеальный трансформатор — это пассивный четырёхполюсник, описывающий формально модель трансформатора без учёта тока холостого хода и ферромагнитного сердечника. Математически это определяется системой уравнений, которая выглядит в H-форме (либо соответствующей ей матрицей):
Гиратор[править | править код]
Гиратор — пассивный четырёхполюсник без потерь, преобразующий входной ток — в выходное напряжение, а входное напряжение — в обратный по знаку (инвертированный) выходной ток (инвертор положительного сопротивления[6]). Математически это описывается системой, которая выглядит в Y-форме (либо соответствующей ей матрицей:
Т.о. гиратор не поглощает и не накапливает энергию, преобразуя комплексное сопротивление нагрузки в сопротивление с обратным знаком и модулем, равным обратному соотношению:
Нуллор[править | править код]
Нуллор — четырехполюсник, аномальный элемент, у которого входные ток и напряжение равны нулю, а выходные ток и напряжение принимают любые, не связанные друг с другом значения[7]. Аномальные элементы используются в ряде случаев при анализе и синтезе электрических цепей.
См. также[править | править код]
Примечания[править | править код]
- ↑ Бакалов, 1989, с. 171.
- ↑ Бессонов, 1978, с. 109.
- ↑ 1 2 Бакалов, 1989, с. 175.
- ↑ Бессонов, 1996, с. 137.
- ↑ 1 2 Бакалов, 1989, с. 174.
- ↑ Бессонов, 1996, с. 149.
- ↑ Кисель, 1986, с. 68.
Литература[править | править код]
- Бессонов Л.А. Теоретические основы электротехники. — М.: Высшая школа, 1978. — 528 с.
- Бессонов Л.А. Теоретические основы электротехники. — М.: Высшая школа, 1996. — 638 с.
- Кисель В.А. Аналоговые и цифровые корректоры. — М.: Радио и связь, 1986. — 184 с.
- Бакалов В.П. Основы теории электрических цепей и электроники. — М.: Радио и связь, 1989. — 528 с. — ISBN 5-256-00265-1.




















































































































































![{\displaystyle U_{1}(1+h_{22}R)=I_{1}[h_{11}(1+h_{22}R)-h_{12}h_{21}R];}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4e1d2830f60649396f21a559ee76389827c3026)





