Алгоритм Суурбалле
Алгоритм Суурбалле — это алгоритм нахождения двух непересекающихся (не имеющих общих рёбер) путей в ориентированном графе с неотрицательными весами, так что оба пути связывают ту же самую пару вершин и имеют минимальную общую длину[1].
Краткое описание алгоритма
[править | править код]Алгоритм предложил Джон Суурбалле и опубликовал в 1974 году[2]. Основная идея алгоритма Суурбалле — использование алгоритма Дейкстры для поиска пути, модификация весов рёбер графа и затем прогон алгоритма Дейкстры второй раз. Выход алгоритма формируется путём комбинирования двух путей, отбрасывания рёбер, которые проходятся в противоположных направлениях этими путями, и использования оставшихся рёбер для формирования путей, которые и служат выходом алгоритма.
Модификация весов подобна модификации весов в алгоритме Джонсона и сохраняет неотрицательность весов, позволяя второму экземпляру алгоритма Дейкстры найти правильный второй путь.
Задачу поиска двух непересекающихся путей с минимальным весом можно рассматривать как частный случай задачи потока минимальной стоимости, где имеется «поток» величиной два с единичной «пропускной способностью» каждого ребра. Алгоритм Суурбалле можно также рассматривать как частный случай алгоритма поиска потока минимальной стоимости, который повторно пропускает максимально возможный поток через кратчайший путь.
Первый найденный алгоритмом Суурбалле путь является кратчайшим путём для начального (нулевого) потока, а второй найденный алгоритмом Суурбалле путь является кратчайшим путём для остаточного графа после пропускания единичного потока через первый путь.
Определения
[править | править код]Пусть G будет взвешенным ориентированным графом с набором вершин V и набором рёбер E (рисунок A). Пусть s будет источником в G, и пусть t будет стоком. Пусть каждое ребро (u,v) в E из вершины u в вершину v имеет неотрицательную цену w(u,v).
Определим d(s,u) как цену кратчайшего пути к вершине u из вершины s в дереве кратчайших путей с корнем в s (рисунок C).
Замечание: Узел и Вершина часто употребляются как синонимы.
Алгоритм
[править | править код]Алгоритм Суурбалле выполняет следующие шаги:
- Ищется дерево кратчайших путей T с корнем в узле s путём прогона алгоритма Дейкстры (рисунок C). Это дерево содержит для любой вершины u кратчайший путь из s в u. Пусть P1 будет наименьшим по стоимости путём из s в t (рисунок B). Рёбра дерева T называются рёбрами дерева, а остальные рёбра (рёбра, отсутствующие на рисунке C), называются рёбрами вне дерева.
- Модифицируем стоимость каждого ребра графа, заменяя цену w(u,v) каждого ребра (u,v) на . Согласно функции модификации цены все рёбра дерева будут иметь стоимость 0, а рёбра вне дерева будут иметь неотрицательные цены. Например,
если , то
если , то - Создаём остаточный граф Gt, образованный из G путём удаления рёбер G по пути P1, которые направлены в s, а затем обращаются направления рёбер с нулевой длиной вдоль пути (рисунок D).
- Находится кратчайший путь в остаточном графе путём прогона алгоритма Дейкстры (рисунок E).
- Отбрасываем обратные рёбра пути P2 из обоих путей. Оставшиеся рёбра путей P1 и P2 образуют из подграфа с двумя исходящими рёбрами из s, двумя входящими рёбрами t, и по одному входящему и одному исходящему ребру в каждой оставшейся вершине. Поэтому этот подграф состоит из двух не имеющих общих рёбер путей из s в t и, возможно, некоторых дополнительных циклов (нулевой длины). Алгоритм возвращает два непересекающихся (по рёбрам) пути из подграфа.
Пример
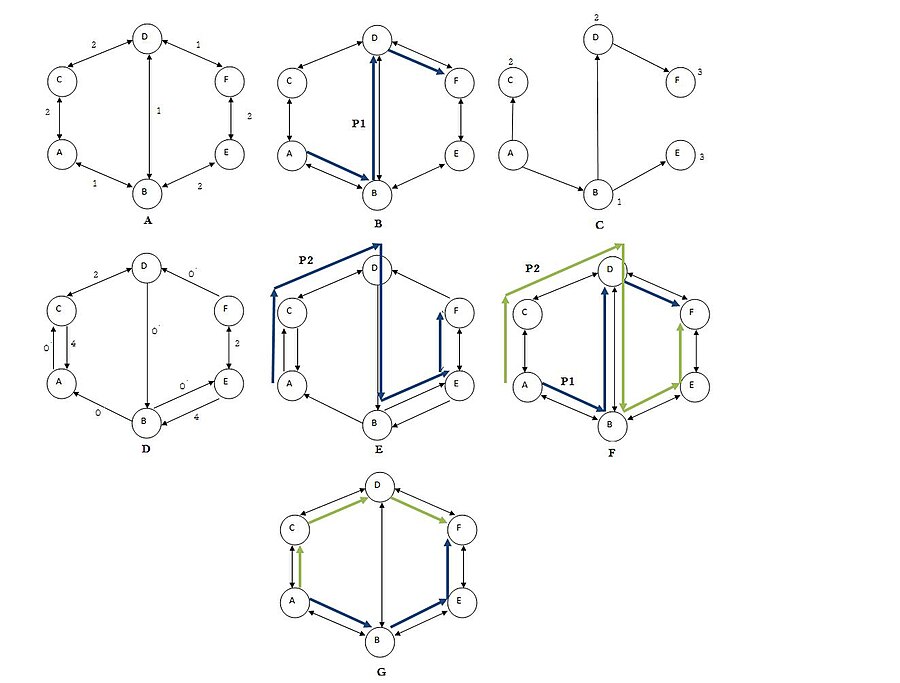
[править | править код]Следующий пример показывает, как алгоритм Суурбалле находит кратчайшую пару непересекающихся путей из A в F.
Рисунок A показывает взвешенный граф G.
Рисунок B вычисляет кратчайший путь P1 из A в F (A-B-D-F).
Рисунок C показывает дерево кратчайших путей T с корнем в A и вычисленные расстояния из A в любую вершину (u).
Рисунок D показывает остаточный граф Gt с обновлёнными ценами каждого ребра и рёбра пути P1 обращены.
Рисунок E вычисляет путь P2 в остаточном графе Gt (A-C-D-B-E-F).
Рисунок F показывает оба пути P1 и P2.
Рисунок G находит кратчайшую пару непересекающихся (по рёбрам) путей путём комбинации рёбер путей P1 и P2 и отбрасыванием общих взаимно противоположных дуг между обоими путями (B-D). Как результат, мы получаем кратчайшую пару непересекающихся путей (A-B-E-F) и (A-C-D-F).
Корректность
[править | править код]Вес любого пути из s в t в модифицированной системе весов равен весу в исходном графе, минус d(s,t). Поэтому два кратчайших непересекающихся пути после модификации весов будут теми же самыми двумя кратчайшими путями в исходном графе, хотя вес будет другой.
Алгоритм Суурбалле можно рассматривать как специальный случай применения методов кратчайшего пути для нахождения потока минимальной стоимости с общим потоком два из s в t. Модификация весов не влияет на найденные алгоритмом пути, только на их вес. Таким образом, корректность алгоритма следует из корректности метода поиска кратчайшего пути.
Анализ и время работы
[править | править код]Этот алгоритм требует двух итераций алгоритма Дейкстры. При использовании фибоначчиевых куч обе итерации могут быть выполнены за время , где и являются числом вершин и рёбер соответственно. Таким образом, те же самые границы приложимы и к алгоритму Суурбалле.
Вариации
[править | править код]Версия алгоритма Суурбалле, как описано выше, находит пути, не имеющие общих рёбер, но, возможно, имеющие общие вершины. Можно использовать тот же алгоритм для нахождения путей, не имеющих общих вершин, путём замены каждой вершины парой смежных вершин, одна со всеми входящими дугами u-in исходной вершины, другая со всеми исходящими дугами u-out. Два пути без общих дуг в этом модифицированном графе обязательно соответствует двум путям без общих вершин в исходном графе и наоборот, так что применение алгоритма Суурбалле к модифицированному графу приводит к построению двух путей без общих вершин в исходном графе. Исходный алгоритм Суурбалле 1974 года был версией с путями без общих вершин и его расширили в 1984 году Суурбалле и Тарьян на версию с путями без общих рёбер[3].
При использовании модифицированной версии алгоритма Дейкстры, который одновременно вычисляет расстояния до каждой вершины t в графах Gt, также можно найти полные длины кратчайших путей из заданной вершины s в любую другую вершину графа за время, пропорциональное работе одного прогона алгоритма Дейкстры.
Замечание: Пара смежных вершин, полученная разбиением вершины, связана ориентированной дугой с нулевой ценой из вершины со входящими дугами в вершину с исходящими дугами. Источником становится s-out, а стоком становится t-in.
Примечания
[править | править код]- ↑ Bhandari, 1999, с. 86–91.
- ↑ Suurballe, 1974, с. 125–145.
- ↑ Suurballe, Tarjan, 1984, с. 325–336.
Литература
[править | править код]- Ramesh Bhandari. Suurballe's disjoint pair algorithms // Survivable Networks: Algorithms for Diverse Routing. — Springer-Verlag, 1999. — С. 86–91. — ISBN 978-0-7923-8381-9.
- Suurballe J. W. Disjoint paths in a network. — 1974. — Т. 4. — С. 125–145. — doi:10.1002/net.3230040204.
- Suurballe J. W., Tarjan R. E. quick method for finding shortest pairs of disjoint paths. — 1984. — Т. 14. — С. 325–336. — doi:10.1002/net.3230140209.
Для улучшения этой статьи желательно:
|