Гибкость стержня

Схемы деформирования и коэффициенты $\mu$ при различных условиях закрепления и способе приложения нагрузки

Гибкость стержня — отношение расчётной длины стержня $l_{0}$ к наименьшему радиусу инерции $i$ его поперечного сечения.

$\lambda ={\frac {l_{0}}{i}}$

Это выражение играет важную роль при проверке сжатых стержней на устойчивость. В частности, от гибкости зависит коэффициент продольного изгиба $\phi$. Стержень с большей гибкостью, при прочих неизменных параметрах, имеет более низкую прочность на сжатие и сжатие с изгибом.

Расчётная длина $l_{0}$ вычисляется по формуле:

$l_{0}=\mu l$, где

$\mu$ — коэффициент, зависящий от условий закрепления стержня, а $l$ — геометрическая длина. Расчётная длина также называется приведённой или свободной.

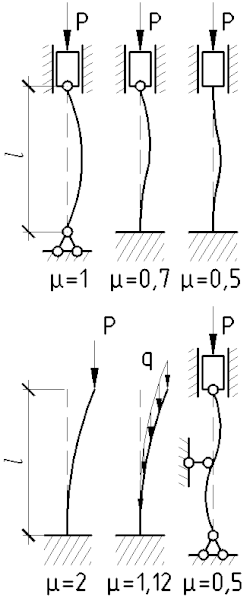
Понятие приведённая длина впервые ввёл Ясинский для обобщения формулы критической силы Эйлера, которую тот выводил для стержня с шарнирно-опертыми концами. Соответственно коэффициент $\mu$ равен при шарнирных концах (основной случай) одному, при одном шарнирном, другом защемлённым $\mu =0.7$, при обоих защемлённых концах $\mu =0,5$. Схемы деформирования и коэффициенты $\mu$ при различных условиях закрепления и способе приложения нагрузки, изображены на рисунке. Также, стоит отметить, что формула Эйлера верна только для элементов большой гибкости, например для стали она применима при гибкостях порядка $\lambda =100$ и выше.

При расчетах элементов железобетонных конструкций к гибкости предъявляются требования по её ограничению. Также, в зависимости от гибкости назначается величина армирования.

В расчётах стальных конструкций гибкость имеет наибольшее значение ввиду большой прочности стали с вытекающей из этого формой элементов (длинные, небольшой площади) из-за чего исчерпание несущей способности по устойчивости наступает до исчерпания запаса прочности по материалу.

Отсюда ввод дополнительных терминов:

1. Условная гибкость
2. Приведённая гибкость
3. Предельная гибкость

Существуют формулы для определения гибкости элементов составных сечений.

Литература

• Беляев Н. М. Сопротивление материалов. — 15-е изд., перераб. — М.: Наука, 1976. — 607 с. — 200 000 экз.
• Горев В. В., Уваров Б. Ю., Филиппов В. В. и др. Металлические конструкции: Учеб. пособие для строит. вузов / Под ред. В. В. Горева. — М.: Высш. шк., 1997. — Т. 1: Элементы стальных конструкций. — 527 с.