Однозначно раскрашиваемый граф

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску

Однозначно раскрашиваемый граф — это k-цветный граф, допускающий только одну (правильную) k-раскраску (с точностью до перестановки цветов).

Примеры[править | править код]

Полный граф является однозначно раскрашиваемым, поскольку существует только одна допустимая раскраска — каждой вершине назначается свой цвет.

Любое k-дерево однозначно раскрашиваемо в (k + 1) цветов. Однозначно раскрашиваемы в 4 цвета планарные графы — это в точности графы Аполлония, то есть планарные 3-деревья[1].

Свойства[править | править код]

Некоторые свойства однозначно k-раскрашиваемого графа G с n вершинами и m рёбрами:

  1. m ≥ (k - 1) n - k(k-1)/2 [2][3]

Связанные концепции[править | править код]

Минимальное несовершенство[править | править код]

Минимально несовершенный граф — это граф, в котором любой подграф является совершенным. Удаление любой вершины из минимально несовершенного графа оставляет однозначно раскрашиваемый подграф.

Однозначная раскраска рёбер[править | править код]

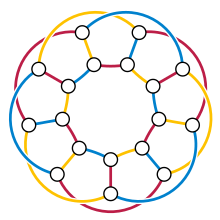
Однозначная 3-раскраска рёбер обобщённого графа Петерсена G(9,2)

Однозначно рёберно-раскрашиваемый граф — это рёберно k-цветный граф, допускающий только одну (правильную) рёберную k-раскраску с точностью до перестановки цветов. Только пути и циклы допускают однозначную рёберную 2-раскраску. Для любого значения k звёзды K1,k являются однозначно рёберно k-раскрашиваемыми графами. Однако Вильсон [4] выдвинул гипотезу, а Томасон[5] доказал, что при k ≥ 4 это единственные члены этого семейства. Существуют, однако, однозначно рёберно 3-раскрашиваемые графы, не попадающий в эту классификацию, как, например, граф треугольной пирамиды.

Если кубический граф однозначно рёберно 3-раскрашиваем, он должен иметь в точности три гамильтонова цикла, образованного рёбрами двух (из трёх) цветов, однако некоторые кубические графы только с тремя гамильтоновыми циклами однозначной рёберной 3-раскраски не имеют[6]. Любой простой планарный кубический граф, допускающий единственную рёберную 3-раскраску, содержит треугольник[1], но Тат[7] заметил, что обобщённый граф Петерсена G(9,2) является непланарным графом без треугольников, однако он однозначно рёберно 3-раскрашиваем. Много лет этот граф был единственным примером таких графов (см.статьи Болобаша[8] и Швенка[9]), но теперь известно бесконечно много непланарных кубических графов без треугольников, имеющих однозначную рёберную 3-раскраску[6].

Однозначная полная раскраска[править | править код]

Однозначно тотально раскрашиваемый граф — это тотально k-цветный граф, допускающий только одну (правильную) тотальную k-раскраску (с точностью до перестановки цветов).

Пустые графы[англ.]*, пути и циклы с длиной, делящейся на 3, являются однозначно тотально раскрашиваемыми графами. Махмудиан и Шокроллахи[10] высказали гипотезу, что только эти графы и составляют семейство.

Некоторые свойства однозначно тотально k-раскрашиваемого графа G с n вершинами:

  1. χ″(G) = Δ(G) + 1 unless G = K2[11]
  2. Δ(G) ≤ 2 δ(G).[11]
  3. Δ(G) ≤ n/2 + 1.[12]

Здесь χ″(G) — тотальное хроматическое число; Δ(G) — максимальная степень, а δ(G) — минимальная степень.

Примечания[править | править код]

  1. ↑ 1 2 Fowler, 1998.
  2. ↑ Truszczyński, 1984.
  3. ↑ Xu, 1990.
  4. ↑ Wilson, 1976.
  5. ↑ Thomason, 1978.
  6. ↑ 1 2 Belcastro, Haas, 2015.
  7. ↑ Tutte, 1976.
  8. ↑ Bollobás, 1978.
  9. ↑ Schwenk, 1989.
  10. ↑ Mahmoodian, Shokrollahi, 1995.
  11. ↑ 1 2 Akbari, Behzad, Hajiabolhassan, Mahmoodian, 1997.
  12. ↑ Akbari, 2003.

Литература[править | править код]

  • S. Akbari. Two conjectures on uniquely totally colorable graphs // Discrete Mathematics. — 2003. — Т. 266, вып. 1-3. — С. 41–45. — doi:10.1016/S0012-365X(02)00797-5.
  • S. Akbari, M. Behzad, H. Hajiabolhassan, E. S. Mahmoodian. Uniquely total colorable graphs // Graphs and Combinatorics. — 1997. — Т. 13, вып. 4. — С. 305–314. — doi:10.1016/S0012-365X(02)00797-5.
  • Sarah-Marie Belcastro, Ruth Haas. Triangle-free uniquely 3-edge colorable cubic graphs // Contributions to Discrete Mathematics. — 2015. — Т. 10, вып. 2. — С. 39–44. — arXiv:1508.06934.
  • Béla Bollobás. Extremal Graph Theory. — Academic Press, 1978. — Т. 11. — (LMS Monographs).
  • Thomas Fowler. Unique Coloring of Planar Graphs. — Georgia Institute of Technology Mathematics Department, 1998.
  • Christopher J. Hillar, Troels Windfeldt. Algebraic characterization of uniquely vertex colorable graphs // Journal of Combinatorial Theory. — 2008. — Т. 98, вып. 2. — С. 400–414. — doi:10.1016/j.jctb.2007.08.004.
  • E. S. Mahmoodian, M. A. Shokrollahi. Combinatorics Advances. — Dordrecht; Boston; London: Kluwer Academic Publishers, 1995. — Т. 329. — С. 321–324. — (Mathematics and its applications).
  • Allen J. Schwenk. Enumeration of Hamiltonian cycles in certain generalized Petersen graphs // Journal of Combinatorial Theory. — 1989. — Т. 47, вып. 1. — С. 53–59. — doi:10.1016/0095-8956(89)90064-6.
  • A. G. Thomason. Advances in Graph Theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977). — 1978. — Т. 3. — С. 259–268. — (Annals of Discrete Mathematics).
  • M. Truszczyński. Finite and Infinite Sets. Vol. I, II. Proceedings of the sixth Hungarian combinatorial colloquium held in Eger, July 6–11, 1981 / András Hajnal, László Lovász, Vera T. Sós. — North-Holland, Amsterdam, 1984. — Т. 37. — С. 733–748. — (Colloq. Math. Soc. János Bolyai).
  • William T. Tutte. Colloquio Internazionale sulle Teorie Combinatorie (Rome, 1973), Tomo I. — Accad. Naz. Lincei, Rome, 1976. — С. 193–199. Atti dei Convegni Lincei, No. 17.. Как процитировано у Белкастро и Хааса (Belcastro, Haas 2015).
  • Shao Ji Xu. The size of uniquely colorable graphs // Journal of Combinatorial Theory. — 1990. — Т. 50, вып. 2. — С. 319–320. — doi:10.1016/0095-8956(90)90086-F.
  • R. J. Wilson. Proc. British Comb. Conf. 1975. — Winnipeg: Utilitas Math., 1976. — С. 696.. Как процитировано у Томасона (Thomason 1978).

Ссылки[править | править код]

Источник — https://ru.wikipedia.org/w/index.php?title=Однозначно_раскрашиваемый_граф&oldid=134097056