Оператор Кэнни
Оператор Кэнни (детектор границ Кэнни, алгоритм Кэнни) в дисциплине компьютерного зрения — оператор обнаружения границ изображения. Был разработан в 1986 году Джоном Кэнни (англ. John F. Canny) и использует многоступенчатый алгоритм для обнаружения широкого спектра границ в изображениях.
Кэнни изучил математическую проблему получения фильтра, оптимального по критериям выделения, локализации и минимизации нескольких откликов одного края. Он показал, что искомый фильтр является суммой четырёх экспонент. Он также показал, что этот фильтр может быть хорошо приближен первой производной Гауссианы. Кэнни ввёл понятие подавления немаксимумов (англ. Non-Maximum Suppression), которое означает, что пикселями границ объявляются пиксели, в которых достигается локальный максимум градиента в направлении вектора градиента.
Хотя его работа была проведена на заре компьютерного зрения, детектор границ Кэнни до сих пор является одним из лучших детекторов. Кроме особенных частных случаев трудно найти детектор, который бы работал существенно лучше, чем детектор Кэнни.
Развитие алгоритма Кэнни
[править | править код]
Для чего используются два порога?
1. Чтобы уменьшить влияние шума для инициализации кривой, используем верхний порог;
2. Чтобы «не потерять хвост», используем нижний порог при прослеживании.

Проверяя, является ли пиксель локальным максимумом вдоль направления градиента, приходится интерполировать «нецелые» пиксели p и r
Целью Кэнни было разработать оптимальный алгоритм обнаружения границ, удовлетворяющий трём критериям:
- хорошее обнаружение (Кэнни трактовал это свойство как повышение отношения сигнал/шум);
- хорошая локализация (правильное определение положения границы);
- единственный отклик на одну границу.
Из этих критериев затем строилась целевая функция стоимости ошибок, минимизацией которой находится «оптимальный» линейный оператор для свёртки с изображением.
Алгоритм детектора границ не ограничивается вычислением градиента сглаженного изображения. В контуре границы оставляются только точки максимума градиента изображения, а не максимальные точки, лежащие рядом с границей, удаляются. Здесь также используется информация о направлении границы для того, чтобы удалять точки именно рядом с границей и не разрывать саму границу вблизи локальных максимумов градиента. Затем с помощью двух порогов удаляются слабые границы. Фрагмент границы при этом обрабатывается как целое. Если значение градиента где-нибудь на прослеживаемом фрагменте превысит верхний порог, то этот фрагмент остается также «допустимой» границей и в тех местах, где значение градиента падает ниже этого порога, до тех пор пока она не станет ниже нижнего порога. Если же на всем фрагменте нет ни одной точки со значением большим верхнего порога, то он удаляется. Такой гистерезис позволяет снизить число разрывов в выходных границах. Включение в алгоритм Кэнни шумоподавления с одной стороны повышает устойчивость результатов, а с другой — увеличивает вычислительные затраты и приводит к искажению и даже потере подробностей границ. Так, например, таким алгоритмом скругляются углы объектов и разрушаются границы в точках соединений.
Основные этапы алгоритма
[править | править код]

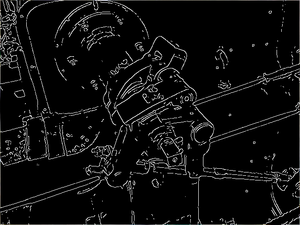
Сглаживание. Размытие изображения для удаления шума. Оператор Кэнни использует фильтр, который может быть хорошо приближен к первой производной гауссианы. = 1.4:
Поиск градиентов. Границы отмечаются там, где градиент изображения приобретает максимальное значение. Они могут иметь различное направление, поэтому алгоритм Кэнни использует четыре фильтра для обнаружения горизонтальных, вертикальных и диагональных ребер в размытом изображении.
Угол направления вектора градиента округляется и может принимать такие значения: 0, 45, 90, 135.

Подавление немаксимумов. Только локальные максимумы отмечаются как границы.
Двойная пороговая фильтрация. Потенциальные границы определяются порогами.
Трассировка области неоднозначности. Итоговые границы определяются путём подавления всех краёв, не связанных с определенными (сильными) границами.
Перед применением детектора обычно преобразуют изображение в оттенки серого, чтобы уменьшить вычислительные затраты. Этот этап характерен для многих методов обработки изображений.



