Координаты Риндлера

В релятивистской физике, координатами Риндлера называется важная и полезная координатная система, представляющая чатсь плоского пространства-времени, также называемого пространством Минковского. Координаты риндлера были введены Вольфгангом Риндлером.

Связь с декартовыми координатами

Для получения кооординат Риндлера естесвенно начать с декартовых координат

$ds^{2}=-dT^{2}+dX^{2}+dY^{2}+dZ^{2},\;\;-\infty <T,X,Y,Z<\infty \;.$

В области $0<X<\infty ,\;-X<T<X$, которая часто называется Клином Риндлера, определим новые координаты, через следующее преобразование

$t=\operatorname {arctanh} (T/X),\;x={\sqrt {X^{2}-T^{2}}},\;y=Y,\;z=Z\;.$

Обратным преобразованием будет

$T=x\,\sinh(t),\;X=x\,\cosh(t),\;Y=y,\;Z=z\;.$

В координатах Риндлера линейный элемент пространства Минксовского переходит в

$ds^{2}=-x^{2}\,dt^{2}+dx^{2}+dy^{2}+dz^{2},\;0<x<\infty ,-\infty <t,y,z<\infty \;.$

Риндлеровские наблюдатели

В новых координатах естественно ввести ковариантное тетрадное поле

$d\sigma ^{0}=-x\,dt,\;\;d\sigma ^{1}=dx,\;\;d\sigma ^{2}=dy,\;\;d\sigma ^{3}=dz\;,$

которому соответствует дуальное поле тетрадных контравариантных векторов

${\vec {e}}_{0}={\frac {1}{x}}\,\partial _{t},\;\;{\vec {e}}_{1}=\partial _{x},\;\;{\vec {e}}_{2}=\partial _{y},\;\;{\vec {e}}_{3}=\partial _{z}\;.$

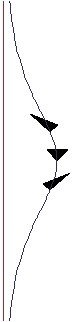
Эти поля описывают локальные Лоренцевы системы отсчёта в касательном пространстве в каждом событии области, покрываемой координатами Риндлера, то есть клина Риндлера. Итегральные кривые поля времениподобного единичного вектора ${\vec {e}}_{0}$ дают времениподобную конгруэнцию, состоящую из мировых линий семейства наблюдателей, называемых наблюдателями Риндлера. В координатах Риндлера их мировые линии изображаются вертикальными координатными линиями $x=x_{0},\;y=y_{0},z=z_{0}$. Используя введённые выше координатные преобразования, легко показать, что к исходных декартовых координатах эти линии превращаются в ветви гипербол.

Мировые линии наболюдателей Риндлера (голубые дуги гипербол) в декартовых координатах.

Как и для любой времениподобной конгруэнции в Лоренцевом многообразии, для этой конгруэнции можно провести кинематическую декомпозицию (см. Уравнение Рэйчаудхури). В рассмтариваемом случае расширение и вращение когруэнции налюдателей Риндлера тождественно равны нулю. Исчезновение тензора расширения влечёт за собой то, что каждый наблюдатель сохраняет постоянное расстояние до ближайших соседей. Исчезновение тензора вращения в свою очередь обозначает, что мировые линии наблюдателей не закручиваются одна вокруг другой.

Вектор ускорения каждого наблюдателя даётся ковариантной производной

$\nabla _{{\vec {e}}_{0}}{\vec {e}}_{0}=1/x\,e_{1}\;.$

Это означает, что каждый риндлеровский наблюдатель ускоряется в направлении $\partial _{x}$, испытывая ускорение постоянной величины, так что их мировые линии — это линии гиперболического движения, лоренцовы аналоги окружностей, то есть линий постоянной первой кривизны и нулевой второй.

Из-за того, что наблюдатели Риндлера не вращаются, их конгруэнция также является ортогональной, то есть существует семействыо гиперповерхностей, в каждой точке которых векторы конгруэнции пропорциональны нормалям эти поверхностей. Ортогональные временные срезы соответствуют $t=t_{0}$; они соответствуют горизонтальным полугиперплоскостям в координатах Риндлера и наклонным полугиперплоскостям в декартовых координатах, проходящих через $T=X=0$ (см. рисунок выше). Положив в линейном элементе $dt=0$, мы видим, что оно описывает обычную евклидову геометрию $d\sigma ^{2}=dx^{2}+dy^{2}+dz^{2},\;0<x<\infty ,\;-\infty <y,z<\infty$. Таким образом, пространственные координаты Риндлера имеют очень простую интерпретацию, совместимую с утвержденем о взаимной стационарности риндлеровских наблюдателей. Далее мы ещё вернёмся к этому свойству "жёсткости".

"Парадоксальное" свойство риндлеровских координат

Отметим, что наблюдатели Риндлера с меньшими значениями координаты $x$ ускоряются сильнее! Это может показаться странным, так как в ньютоновой физике наблюдатели, сохраняющие постоянное расстояние друг от друга, должны испытывать одно и то же ускорение. Но в релятивистской физике задний конец "абсолютно твёрдого" стержня, ускоряемого в направлении собственной протяжённости приложенной силой, должен ускоряться чуть сильнее, чем его передний конец.

Это явление является основанием хорошо известного "парадокса". Тем не менее, это просто следствие релятивистской кинематики. Один из вариантов показать это — рассмотреть величину вектора ускорения как кривизну соответствующей мировой линии. Но мировые линии риндлеровских наблюдателей явдляются аналогами семейства концентрических окружностей в евклидовой плоскости, так что мы имеем дело с Лоренцевым аналогом изветстного факта: в семействе концентрических окружностей внутернние окружности отклоняются от прямой на единице дилны дуги быстрее, чем внешние.

Наблюдатели Минковского

Мировые линии наболюдателей Минковского (голубые дуги гипербол) в координатах Риндлера. Горизонт риндлера выделен красным цветом.

также стоит ввести алтернативную систему отсчёта, даваемую стандартным выбором тетрад в координатах Минковского

${\vec {f}}_{0}=\partial _{T},\;{\vec {f}}_{1}=\partial _{X},\;{\vec {f}}_{2}=\partial _{Y},\;{\vec {f}}_{3}=\partial _{Z}\;.$

Преобразуя эти векторные поля к риндлеровским координатам, получаем, что в клине Риндлера эта система отсчёта имеет вид

${\vec {f}}_{0}={\frac {\cosh(t)}{x}}\,\partial _{t}-\sinh(t)\,\partial _{x}\;,$

${\vec {f}}_{1}=-{\frac {\sinh(t)}{x}}\,\partial _{t}+\cosh(t)\,\partial _{x}\;,$

${\vec {f}}_{2}=\partial _{y},\;{\vec {f}}_{3}=\partial _{z}\;.$

Осуществляя кинематическое разложение времениподобной конгруэнции, определяемой векторным полем ${\vec {f}}_{0}$, мы очевидно получаем нулевые расширение и вращение, а дополнительно и отсутствие ускорения $\nabla _{{\vec {f}}_{0}}{\vec {f}}_{0}=0$. Другими словами, эта конгруэнция — геодезическая; соответствующие наблюдатели находятся в состоянии свободного падения. В исходной декартовой системе координат эти наблюдатели, называемые наблюдателями Минковского, находятся в покое.

В координатах Риндлера мировые линии наблюдателей Минковского являются гиперболическими дугами, асимптотическеи приближающимися к координатной плоскости $x=0$. В частности, в риндлеровских кооординатах мировая линия наблюдателя Минковского, проходящая через событие $t=t_{0},\;x=x_{0},\;y=y_{0},\;z=z_{0}$ будет иметь вид

$t=\operatorname {arctanh} (s/x_{0}),\;x={\sqrt {x_{0}^{2}-s^{2}}},\;y=y_{0},\;z=z_{0},\;-x_{0}<s<x_{0}\;,$

где $s$ — собственное время этого наблдюателя. Отметим, что координаты Риндлера покрывают лишь малую часть от полной истории этого наблюдателя! Это непосредственно показывает, что координаты Риндлера не являются геодезически полными: времениподобные геодезические линии выходят из области, покрываемой этими координатами, за конечное собственное время. Естественно, этого и следовало ожидать, так как координаты Риндлера покрывают лишь часть исходных декартовых координат, которые являются геодезически полными.

На рисунке изображён случай $x_{0}=1$ и световые конусы при $s=-{\frac {1}{2}},\;0,\;{\frac {1}{2}}$.

The Rindler horizon

The Rindler coordinate chart has a coordinate singularity at $x=0$, where the metric tensor (expressed in the Rindler coordinates) has vanishing determinant. This happens because as $x\rightarrow 0$ the acceleration of the Rindler observers diverges. As we can see from the figure illustrating the Rindler wedge, the locus $x=0$ in the Rindler chart corresponds to the locus $T^{2}=X^{2},\;X>0$ in the Cartesian chart, which consists of two null half-planes, each ruled by a null geodesic congruence.

For the moment, we simply consider the Rindler horizon as the boundary of the Rindler coordinates. Later we will see that it is in fact analogous in some important respects, to the event horizon of a black hole.

Geodesics

The geodesic equations in the Rindler chart are easily obtained from the geodesic Lagrangian; they are

${\ddot {t}}+{\frac {2}{x}}\,{\dot {x}}\,{\dot {t}}=0,\;{\ddot {x}}+x\,{\dot {t}}^{2}=0,\;{\ddot {y}}=0,\;{\ddot {z}}=0$

Of course, in the original Cartesian chart, the geodesics appear as straight lines, so we could easily obtain them in the Rindler chart using our coordinate transformation. However, it is instructive to obtain and study them independently of the original chart, and we shall do so in this section.

Some representative null geodesics (black hyperbolic semicircular arcs) projected into the spatial hyperslice t=0 of the Rindler observers. The Rindler horizon is shown as a magenta plane.

From the first, third, and fourth we immediately obtain the first integrals

${\dot {t}}={\frac {E}{x^{2}}}\;\;{\dot {y}}=P,\;\;{\dot {z}}=Q$

But from the line element we have $\epsilon =-x^{2}\,{\dot {t}}^{2}+{\dot {x}}^{2}+{\dot {y}}^{2}+{\dot {z}}^{2}$ where $\epsilon =-1,\,0,\,1$ for timelike, null, and spacelike geodesics, respectively. This gives the fourth first integral, namely

${\dot {x}}^{2}=\left(-\epsilon +{\frac {E^{2}}{x^{2}}}\right)-P^{2}-Q^{2}$.

This suffices to give the complete solution of the geodesic equations.

In the case of null geodesics, from ${\frac {E^{2}}{x^{2}}}-P^{2}-Q^{2}$ with nonzero E, we see that the x coordinate ranges over the interval $0<x<{\frac {E}{\sqrt {P^{2}+Q^{2}}}}$.

The complete seven parameter family giving any null geodesic through any event in the Rindler wedge, is

${\begin{matrix}t-t_{0}&=&\operatorname {arctanh} \left({\frac {s\,(P^{2}+Q^{2})-{\sqrt {E^{2}-(P^{2}+Q^{2})\,x_{0}^{2}}}}{E}}\right)\\&&+~\operatorname {arctanh} \left({\frac {\sqrt {E^{2}-(P^{2}+Q^{2})\,x_{0}^{2}}}{E}}\right)\end{matrix}}$

$x={\sqrt {x_{0}^{2}+2\,s\,{\sqrt {E^{2}-(P^{2}+Q^{2})\,x_{0}^{2}}}-s^{2}\,(P^{2}+Q^{2})}}$

$y-y_{0}=P\,s;\;\;z-z_{0}=Q\,s$

Plotting the tracks of some representative null geodesics through a given event (that is, projecting to the hyperslice $t=0$), we obtain a picture which looks suspiciously like the family of all semicircles through a point and orthogonal to the Rindler horizon! (See the figure.)

The Fermat metric

The fact that in the Rindler chart, the projections of null geodesics into any spatial hyperslice for the Rindler observers are simply semicircular arcs can be verified directly from the general solution just given, but there is a very simple way to see this. A static spacetime is one in which a vorticity-free timelike Killing vector field can be found. In this case, we have a uniquely defined family of (identical) spatial hyperslices orthogonal to the corresponding static observers (who need not be inertial observers). This allows us to define a new metric on any of these hyperslices which is conformally related to the original metric inherited from the spacetime, but with the property that geodesics in the new metric (note this is a Riemannian metric on a Riemannian three-manifold) are precisely the projections of the null geodesics of spacetime. This new metric is called the Fermat metric, and in a static spacetime endowed with a coordinate chart in which the line element has the form

$ds^{2}=g_{00}\,dt^{2}+g_{jk}\,dx^{j}\,dx^{k},\;\;1\leq j,\;k\leq 3$

the Fermat metric on t = 0 is simply

$d\rho ^{2}={\frac {g_{jk}\,dx^{j}\,dx^{k}}{-g_{00}}}$

(where the metric coeffients are understood to be evaluated at t = 0).

In the Rindler chart, the timelike translation $\partial _{t}$ is such a Killing vector field, so this is a static spacetime (not surprisingly, since Minkowski spacetime is of course trivially a static vacuum solution of the Einstein field equation). Therefore, we may immediately write down the Fermat metric for the Rindler observers:

$d\rho ^{2}={\frac {dx^{2}+dy^{2}+dz^{2}}{x^{2}}},\;\;0<x<\infty ,\;\;-\infty <y,z<\infty$

But this is the well-known line element of hyperbolic three-space H³ in the upper half space chart! This is closely analogous to the well known upper half plane chart for the hyperbolic plane H², which is familiar to generations of complex analysis students in connection with conformal mapping problems (and much more), and many mathematically minded readers already known that the geodesics of H² in the upper half plane model are simply semicircles (orthogonal to the circle at infinity represented by the real axis).

Symmetries

Since the Rindler chart is a coordinate chart for Minkowksi spacetime, we expect to find ten linearly independent Killing vector fields. Indeed, in the Cartesian chart we can readily find ten linearly independent Killing vector fields, generating respectively one parameter subgroups of time translation, three spatials, three rotations and three boosts. Together these generate the (proper isochronous) Poincaré group, the symmetry group of Minkowski spacetime.

However, it is instructive to write down and solve the Killing vector equations directly. We obtain four familiar looking Killing vector fields

$\partial _{t},\;\;\partial _{y},\;\;\partial _{z},\;\;-z\,\partial _{y}+y\,\partial _{z}$

(time translation, spatial translations orthogonal to the direction of acceleration, and spatial rotation orthogonal to the direction of acceleration) plus six more:

$\exp(\pm t)\,\left({\frac {y}{x}}\,\partial _{t}\pm \left(y\,\partial _{x}-x\,\partial _{y}\right)\right)$

$\exp(\pm t)\,\left({\frac {z}{x}}\,\partial _{t}\pm \left(z\,\partial _{x}-x\,\partial _{z}\right)\right)$

$\exp(\pm t)\,\left({\frac {1}{x}}\,\partial _{t}\pm \partial _{x}\right)$

(where the signs are chosen consistently + or -). We leave it as an exercise to figure out how these are related to the standard generators; here we wish to point out that we must be able to obtain generators equivalent to $\partial _{T}$ in the Cartesian chart, yet the Rindler wedge is obviously not invariant under this translation. How can this be? The answer is that like anything defined by a system of partial differential equations on a smooth manifold, the Killing equation will in general have locally defined solutions, but these might not exist globally. That is, with suitable restrictions on the group parameter, a Killing flow can always be defined in a suitable local neighborhood, but the flow might not be well-defined globally. This has nothing to do with Lorentzian manifolds per se, since the same issue arises in the study of general smooth manifolds.

Notions of distance

One of the many valuable lessons to be learned from a study of the Rindler chart is that there are in fact several distinct (but reasonable) notions of distance which can be used by the Rindler observers.

Operational meaning of the radar distance between two Rindler observers (navy blue vertical lines). The Rindler horizon is shown at left (red vertical line). The world line of the radar pulse is also depicted, together with the (properly scaled) light cones at events A, B, C.

The first is the one we have tacitly employed above: the induced Riemannian metric on the spatial hyperslices $t=t_{0}$. We will call this the ruler distance since it corresponds to this induced Riemannian metric, but its operational meaning might not be immediately apparent.

From the standpoint of physical measurement, a more natural notion of distance between two world lines is the radar distance. This is computed by sending a null geodesic from the world line of our observer (event A) to the world line of some small object, whereupon it is reflected (event B) and returns to the observer (event C). The radar distance is then obtained by dividing the round trip travel time, as measured by an ideal clock carried by our observer.

(In Minkowski spacetime, fortunately, we can ignore the possibility of multiple null geodesic paths between two world lines, but in cosmological models and other applications things are not so simple! We should also caution against assuming that this notion of distance between two observers gives a notion which is symmetric under interchanging the observers!)

In particular, let us consider a pair of Rindler observers with coordinates $x=x_{0},\;y=0,\;z=0$ and $x=x_{0}+h,\;y=0,\;z=0$ respectively. (Note that the first of these, the trailing observer, is accelerating a bit harder, in order to keep up with the leading observer). Setting $dy=dz=0$ in the Rindler line element, we readily obtain the equation of null geodesics moving in the direction of acceleration:

$t-t_{0}=\log(x/x_{0})$

Therefore, the radar distance between these two observers is given by

$x_{0}\,\log \left(1+{\frac {h}{x_{0}}}\right)=h-{\frac {h^{2}}{2\,x_{0}}}+O\left(h^{3}\right)$

This is a bit smaller than the ruler distance, but for nearby observers the discrepancy is negligible.

A third possible notion of distance is this: our observer measures the angle subtended by a unit disk placed on some object (not a point object!), as it appears from his location. We call this the optical diameter distance. Because of the simple character of null geodesics in Minkowski spacetime, we can readily determine the optical distance between our pair of Rindler observers (aligned with the direction of acceleration). From a sketch it should be plausible that the optical diameter distance scales like $h+{\frac {1}{x_{0}}}+O\left(h^{3}\right)$. Therefore, in the case of a trailing observer estimating distance to a leading observer (the case $h>0$), the optical distance is a bit larger than the ruler distance, which is a bit larger than the radar distance. The reader should now take a moment to consider the case of a leading observer estimating distance to a trailing observer!

There are other notions of distance, but the main point is clear: while the values of these various notions will in general disagree for a given pair of Rindler observers, they all agree that every pair of Rindler observers maintains constant distance. The fact that very nearby Rindler observers are mutually stationary follows from the fact, noted above, that the expansion tensor of the Rindler congruence vanishes identically. However, we have shown here that in various senses, this rigidity property holds at larger scales. This is truly a remarkable rigidity property, given the well-known fact that in relativistic physics, no rod can be accelerated rigidly (and no disk can be spun up rigidly) --- at least, not without sustaining inhomogeneous stresses. The easiest way to see this is to observe that in Newtonian physics, if we "kick" a rigid body, all elements of matter in the body will immediately change their state of motion. This is of course incompatible with the relativistic principle that no information having any physical effect can be transmitted faster than the speed of light.

It follows that if a rod is accelerated by some external force applied anywhere along its length, the elements of matter in various different places in the rod cannot all feel the same magnitude of acceleration if the rod is not to extend without bound and ultimately break. In other words, an accelerated rod which does not break must sustain stresses which vary along its length. Furthermore, in any thought experiment with time varying forces, whether we "kick" an object or try to accelerate it gradually, we cannot avoid the problem of avoiding mechanical models which are inconsistent with relativistic kinematics (because distant parts of the body respond too quickly to an applied force).

Returning to the question of the operational significance of the ruler distance, we see that this should be the distance which our observers will obtain should they very slowly pass from hand to hand a small ruler which is repeatedly set end to end. But justifying this interpretation in detail would require some kind of material model.

See also

• Bell's spaceship paradox, for a sometimes controversial subject often studied using Rindler coordinates.
• Born coordinates, for another important coordinate system adapted to the motion of certain accelerated observers in Minkowski spacetime.
• Congruence (general relativity)
• Ehrenfest paradox, for a sometimes controversial subject often studied using Born coordinates.
• Frame fields in general relativity
• General relativity resources
• Raychaudhuri equation
• Unruh effect

References

Useful background:

• Boothby, William M. An Introduction to Differentiable Manifolds and Riemannian Geometry. — New York: Academic Press, 1986. — ISBN ISBN 0-12-116052-1. See Chapter 4 for background concerning vector fields on smooth manifolds.

• Frankel, Theodore. Gravitational Curvature: an Introduction to Einstein's Theory. — San Francisco : W. H. Freeman, 1979. — ISBN ISBN 0-7167-1062-5. See Chapter 8 for a derivation of the Fermat metric.

Rindler coordinates:

• Misner, Charles; Thorne, Kip S. & Wheeler, John Archibald. Gravitation. — San Francisco: W. H. Freeman, 1973. — ISBN ISBN 0-7167-0344-0. See Section 6.6.

• Rindler, Wolfgang. Relativity: Special, General and Cosmological. — Oxford: Oxford University Press, 2001. — ISBN ISBN 0-19-850836-0.

Rindler horizon:

• Jacobson, Ted; and Parenti, Renaud (2003). "Horizon Entropy". Found. Phys. 33: 323–348.{{cite journal}}: Википедия:Обслуживание CS1 (множественные имена: authors list) (ссылка) eprint version

• Barceló, Carlos; Liberati, Stefano; and Visser, Matt. Analogue Gravity  (неопр.). Living Reviews in Relativity. Дата обращения: 6 мая 2006.