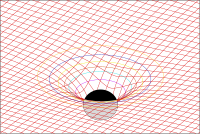
Пространство-время
Простра́нство-вре́мя (простра́нственно-временно́й конти́нуум) — физическая модель, дополняющая пространство равноправным[1] временны́м измерением и таким образом создающая теоретико-физическую конструкцию, которая называется пространственно-временным континуумом. Пространство-время непрерывно и с математической точки зрения представляет собой многообразие с лоренцевой метрикой.
В нерелятивистской классической механике использование Евклидова пространства, не зависящего от одномерного времени, вместо пространства-времени уместно, так как время рассматривается как всеобщее и неизменное, будучи независимым от состояния движения наблюдателя. В случае релятивистских моделей время не может быть отделено от трёх измерений пространства, потому что наблюдаемая скорость, с которой течёт время для объекта, зависит от его скорости относительно наблюдателя, а также от силы гравитационного поля, которое может замедлить течение времени.
В космологии и релятивистской физике вообще концепция пространства-времени объединяет пространство и время в одну абстрактную Вселенную. Математически она является многообразием, состоящим из «событий», описанных системой координат. Обычно требуется три пространственных измерения (длина, ширина, высота) и одно временное измерение (время). Измерения — независимые составляющие координатной сетки, необходимые для локализации точки в некотором ограниченном «пространстве». Например, на Земле широта и долгота — две независимые координаты, которые вместе однозначно определяют положение. В пространстве-времени координатная сетка, которая простирается в 3+1 измерениях, локализует события (вместо просто точки в пространстве), то есть время добавляется как ещё одно измерение в координатной сетке. Таким образом, координаты определяют, где и когда происходят события. Однако единая природа пространства-времени и его независимость от выбора координат позволяют предположить, что чтобы выразить временную координату в одной системе координат, необходимы как временная, так и пространственная координаты в другой системе координат. В отличие от обычных пространственных координат, в пространстве-времени возникает понятие светового конуса, накладывающее ограничения на допустимые координаты, если одна из них везде должна быть временной. Эти ограничения жёстко связаны с особой математической моделью, которая отличается от евклидова пространства с его очевидной симметрией.
В соответствии с теорией относительности, Вселенная имеет три пространственных измерения и одно временное измерение, и все четыре измерения органически связаны в единое целое, являясь почти равноправными и в определённых рамках (см. примечания ниже) способными переходить друг в друга при смене наблюдателем системы отсчёта.
В рамках общей теории относительности пространство-время имеет и единую динамическую природу, а его взаимодействие со всеми остальными физическими объектами (телами, полями) и есть гравитация. Таким образом, теория гравитации в рамках ОТО и других метрических теорий гравитации есть теория пространства-времени, полагаемого не плоским, а способным динамически менять свою кривизну.
До начала двадцатого века время полагалось независимым от состояния движения, протекающим с постоянной скоростью во всех системах отсчёта; однако затем эксперименты показали, что время замедляется при больших скоростях одной системы отсчёта относительно другой. Это замедление, названное релятивистским замедлением времени, объясняется в специальной теории относительности. Замедление времени подтвердили многие эксперименты, такие как релятивистское замедление распада мюонов в потоке космических лучей и замедление атомных часов на борту космического челнока, ракеты и самолётов относительно установленных на Земле часов. Длительность времени поэтому может меняться в зависимости от событий и системы отсчёта.
Термин пространство-время получил широкое распространение далеко за пределами трактовки пространства-времени с нормальными 3+1 измерениями. Это действительно соединение пространства и времени. Другие предложенные теории пространства-времени включают дополнительные измерения, обычно пространственные, но существуют некоторые умозрительные теории, включающие дополнительные временные измерения, и даже такие, которые включают измерения, не являющиеся ни временными, ни пространственными (например, суперпространство)[2]. Вопрос о том, сколько измерений необходимо для описания Вселенной, открыт до сих пор. Умозрительные теории, такие как теория струн, предсказывают 10 или 26 измерений (с М-теорией, предсказывающей 11 измерений: 10 пространственных и 1 временное), но существование более четырёх измерений имело бы значение только на субатомном уровне.
Введение[править | править код]



Нерелятивистская классическая механика рассматривает время как универсальную величину измерения, которая является однородной во всем пространстве и которая отделена от пространства. Классическая механика предполагает, что время имеет постоянную скорость течения, которая не зависит от состояния движения наблюдателя или чего-либо внешнего[3].
В контексте специальной теории относительности время не может быть отделено от трёх измерений пространства, поскольку наблюдаемая скорость течения времени объекта зависит от скорости объекта относительно наблюдателя. Общая теория относительности, кроме того, даёт объяснение того, как гравитационные поля могут замедлять течение времени для объекта, наблюдаемого за пределами этого поля.
В обычном пространстве позиция определяется тремя числами, известными как размерность. В декартовой системе координат они называются x, y и z. Позиция в пространстве-времени называется событием, и требует указания четырёх чисел: трёхмерное местоположение в пространстве, а также положение во времени (рис. 1). Таким образом, пространство-время четырёхмерное. Событие — то, что происходит в определённое мгновение в одной точке пространства-времени, представленной набором координат: x, y, z и t.
Слово «событие», используемое в теории относительности, не следует путать с использованием слова «событие» в обычном разговоре, где оно может означать нечто вроде концерта, спортивного события или сражения. Это не математические «события» в том смысле, в котором это слово используется в теории относительности, потому что они имеют конечную и ненулевую длительность. В отличие от таких событий как фейерверки или молнии, математические события имеют нулевую продолжительность и представляют собой единственную точку пространства-времени.
Путь частицы через пространство-время можно рассматривать как последовательность событий. Ряд событий можно связать вместе, чтобы сформировать линию, которая представляет движение этой частицы в пространстве-времени. Эта линия называется мировой линией частицы[4] : 105.
Математически пространство-время является многообразием, то есть локально «плоским» рядом с каждой точкой так же, как при достаточно малых масштабах глобус кажется плоским.[5] Очень большой масштабный коэффициент (обычно называемый скоростью света) соотносит расстояния, измеренные в пространстве, с расстояниями, измеренными во времени. Величина этого масштабного коэффициента (почти 300 000 км в пространстве, что эквивалентно 1 секунде во времени), а также тот факт, что пространство-время является многообразием, означает, что при обычных, нерелятивистских скоростях и на обычных расстояниях на человеческом уровне мало кто может заметить отличия от евклидового пространства. Только с появлением высокоточных научных измерений в середине XIX века, таких как эксперимент опыт Физо и эксперимент Майкельсона, возникли загадочные расхождения между наблюдениями и прогнозами на основе неявного предположения о евклидовом пространстве.[6]
В специальной теории относительности термин «наблюдатель», в большинстве случаев, означает систему отсчёта, в которой производятся измерения объектов или событий. Это использование значительно отличается от обычного значения термина. Системы отсчёта являются нелокальными конструкциями, и в соответствии с таким использованием термина не имеет смысла говорить о том, что наблюдатель имеет какое-либо положение. На рис. 1-1 представьте, что рассматриваемая система отсчёта оснащена плотной решёткой часов, синхронизированной в этой системе отсчёта, которая неограниченно продолжается на протяжении трёх измерений пространства. Любое конкретное место решётки не имеет значения. Часовая решётка часов используется для определения времени и положения событий, происходящих во всей системе отсчёта. Термин наблюдатель относится ко всему набору часов, связанным с одной инерциальной системой отсчёта.[7]: 17-22 В этом идеализированном случае каждая точка пространства имеет связанные с ней часы, и поэтому часы регистрируют каждое событие мгновенно, без задержки между событием и его записью. Однако реальный наблюдатель увидит задержку между испусканием сигнала и его обнаружением из-за конечности скорости света. При синхронизации часов учитывается время распространения сигнала и часы корректируются на величину времени его распространения.
Во многих книгах по специальной теории относительности, особенно более старых, слово «наблюдатель» используется в более обычном понимании. Обычно смысл термина ясен из контекста.
Физики различают понятия измерять и наблюдать (после установления задержки распространения сигнала) от того, что визуально видно без таких корректировок. Ошибки в понимании отличий того, что измеряется/наблюдается от того, что видится, является источником многих ошибок среди начинающих изучение теории относительности.[8]
Пространство-время в специальной теории относительности[править | править код]
Интервал[править | править код]
В трёх измерениях расстояние между двумя точками может быть определено с использованием теоремы Пифагора:
Хотя два наблюдателя могут измерять положение x, y и z двух точек, используя разные системы координат, расстояние между точками будет для обоих одинаковым (при условии, что они измеряют с использованием тех же единиц). Расстояние таким образом «инвариант».
Однако в специальной теории относительности расстояние между двумя точками больше не сохраняется при измерении двумя разными наблюдателями из-за сокращения Лоренца, если один из наблюдателей движется. Ситуация ещё больше осложняется, если две точки разделены и расстоянием и временем. Например, если один наблюдатель видит, что два события происходят в одном и том же месте, но в разное время, наблюдатель, движущийся относительно первого, увидит два события, происходящие в разных местах. Таким образом, для измерения эффективного «расстояния» между двумя событиями придётся использовать другой способ измерения.
В четырёхмерном пространстве-времени аналогом расстояния является «интервал». Хотя время входит в четвёртое измерение, оно трактуется иначе, чем пространственные измерения и поэтому пространство Минковского существенно отличается от четырёхмерного евклидова пространства. Основная причина слияния пространства и времени в пространство-время состоит в том, что пространство и время не являются инвариантными, то есть в соответствующих условиях разные наблюдатели будут не согласны относительно промежутка времени (из-за замедления времени) или расстояния (из-за лоренцева сокращения длины) между двумя событиями. Но специальная теория относительности обеспечивает новый инвариант, называемый интервалом пространства-времени, который объединяет расстояния в пространстве и во времени. Все наблюдатели, которые измеряют время и расстояние, получат один и тот же интервал пространства-времени между любыми двумя событиями. Предположим, что наблюдатель измеряет два события, разделённые во времени на и в пространстве на . Тогда интервал пространства-времени между двумя событиями, разделёнными расстоянием в пространстве и в -координате:
- , или для трёх пространственных измерений, [9]
Постоянная , скорость света, преобразует единицы измерения времени (в секундах) в единицы измерения расстояния (в метры).
Примечание по обозначениям: Хотя для краткости часто встречаются интервальные выражения, выраженные без дельт, включая большинство следующих обсуждений, следует понимать, что в общем случае означает и т. д. Нам всегда интересны «изменения» пространственных или временных значений координат, относящихся к двум событиям, и, поскольку нет выделенного начала системы отсчёта, конкретные значения координат не имеют существенного значения.

Уравнение выше похоже на теорему Пифагора, за исключением знака минус между выражениями и . Заметим также, что интервал пространства-времени представляет собой величину , а не . Причина в том, что в отличие от расстояний в евклидовой геометрии интервалы в пространстве-времени Минковского могут быть отрицательными. Вместо того, чтобы иметь дело с квадратными корнями из отрицательных чисел, физики обычно рассматривают как отдельный символ сам по себе, а не квадрат величины.
Из-за знака минус интервал пространства-времени между двумя отдельными событиями может быть равен нулю. Если является положительным, интервал пространства-времени является времениподобным, что означает, что два события разделяются больше временем, чем пространством. Если отрицательный, интервал пространства-времени является пространственно-подобным, что означает, что два события разделены больше пространством, чем временем. Пространственно-временные интервалы равны нулю, когда . Другими словами, интервал чего-то движущегося со скоростью света между двумя событиями на мировой линии равен нулю. Такой интервал называется светоподобным или нулевым. Фотон, попавший в наш глаз от далёкой звезды, не имеет возраста, несмотря на то, что (с нашей точки зрения) провёл годы в пути.
Диаграмма пространства-времени обычно рисуется только с одной пространственной и одной временной осью. На рис. 2-1 представлена пространственно-временная диаграмма, иллюстрирующая мировые линии (то есть пути в пространстве-времени) двух фотонов A и B, вышедших из одного и того же события и идущих в противоположных направлениях. Кроме того, C иллюстрирует мировую линию объекта с досветовой скоростью. Вертикальная координата времени имеет масштаб , так что она имеет те же единицы (метры), что и пространственная ось. Поскольку фотоны движутся со скоростью света, их мировые линии имеют наклон ± 1. Другими словами, каждый метр, который фотон перемещается влево или вправо, требует приблизительно 3,3 наносекунды времени.
Примечание по обозначениям: В литературе по теории относительности есть две формы записи:
- и
Эти формы записи связаны с сигнатурой метрики (+ − − −) и (− + + +). Отличие состоит в расположении координаты времени. Обе формы широко используются в научном поле.
Система отсчёта[править | править код]


При сравнении измерений, выполненных движущимися относительно друг друга наблюдателями в разных инерциальных системах отсчёта, полезно работать с системами отсчёта в стандартной конфигурации. На рис.2-2 показаны две движущиеся относительно друг друга галлиеевы системы отсчёта (то есть обычные трёхмерные пространственные системы отсчёта). Система S принадлежит первому наблюдателю O, а система S' принадлежит второму наблюдателю O'.
- Оси x, y, z системы S ориентированы параллельно относительно соответствующих осей системы S'.
- Система S' перемещается в направлении оси x системы S с постоянной скоростью v, измеренной в системе S.
- Начала отсчёта систем S и S 'совпадают, когда время t= 0 для системы S и t' = 0 для системы S'.[4]:107
Рис. 2‑3a представляет собой повёрнутый в другом направлении рис. 2‑2. Рис. 2‑3b иллюстрирует диаграмму пространства-времени с точки зрения наблюдателя О. Поскольку S и S' находятся в стандартной конфигурации, их начала отсчёта совпадают в момент t = 0 в системе S и t′ = 0 в системе S'. Ось ct 'проходит через события в системе S', которые имеют x′ = 0. Но точки с x′ = 0 движутся в направлении x системы S со скоростью v, так что они не совпадают с осью ct в любое отличное от нуля время. Поэтому ось ct' наклоняется относительно оси ct на угол θ, заданный формулой
Ось x' также наклоняется относительно оси x. Чтобы определить угол этого наклона, напомним, что наклон мировой линии светового импульса всегда ±1. Рис. 2‑3c представляет собой диаграмму пространства-времени с точки зрения наблюдателя O'. Событие P представляет собой излучение светового импульса при x′ = 0, ct′ = −a. Импульс отражается от зеркала, расположенного на расстоянии a от источника света (событие Q), и возвращается к источнику света в x′ = 0, ct′ = a (событие R).
Те же события P, Q, R нарисованы на рис. 2‑3b в системе наблюдателя O. Пути света имеют наклоны = 1 и −1 так что △PQR образует прямоугольный треугольник. Так как OP = OQ = OR, угол между x' и x должен быть также θ.
В то время как покоящаяся система отсчёта имеет пространственные и временные оси, которые пересекаются под прямым углом, движущаяся система отсчёта имеет острый угол между осями. Но фактически системы отсчёта эквивалентны. Асимметрия рисунка обусловлена неизбежными искажениями того, как координаты пространства-времени отображаться на прямоугольную систему координат, и это следует считать не более странным, чем то, как на земной проекция Меркатора относительные размеры площади поверхности вблизи полюсов (Гренландия и Антарктида) сильно больше относительно площади поверхности вблизи экватора.
Световой конус[править | править код]

На рисунке 2-4 событие O находится в начале отсчёта пространственно-временной диаграммы, две диагональные линии представляют все события, которые имеют нулевой интервал пространства-времени относительно события в начале отсчёта. Эти две линии образуют то, что называется световым конусом события O, поскольку добавление второго пространственного измерения (рис. 2‑5) приводит к появлению двух конусов, которые касаются друг друга вершинами в O. Один конус распространяется в будущее (t>0), а другой — в прошлое (t<0).

Световой (двойной) конус относительно его вершины делит пространство-время на отдельные области. Внутренняя часть светового конуса будущего (верхняя часть, future light cone) состоит из всех событий, которые отделены от вершины бо́льшим «временным» расстоянием, чем необходимо, чтобы пересечь их «пространственное расстояние» на скорости света; эти события составляют времениподобное будущее события O. Аналогично, времениподобное прошлое включает в себя внутренние события светового конуса прошлого (нижняя часть, past light cone). Таким образом, времениподобные интервалы Δct больше, чем Δx, что делает времениподобные интервалы положительными. Область, внешняя по отношению к световому конусу, состоит из событий, которые отделены от события О большим пространством, чем можно пересечь на скорости света за заданное время. Эти события включают в себя так называемую пространственно-подобную область события О, обозначенную на рис. 2-4 как «где-то ещё» (elsewhere). События на самом световом конусе называются светоподобными (или нуль отделяемыми) от O. Из-за инвариантности интервала пространства-времени все наблюдатели будут иметь один и тот же световой конус для любого заданного события и, таким образом, согласятся с таким общим разделением пространства-времени.[10]:220
Световой конус играет важную роль в концепции причинности. Возможно, что досветовой сигнал перемещается от положения и времени O к положению и времени D (рис.2-4). Следовательно, событие O может быть причинное влияние события D. Световой конус будущего содержит все события, на которые может оказывать причинное влияние O. Аналогично, возможно, что досветовой сигнал идёт от положения и времени A к положению и времени O. Световой конус прошлого содержит все события, которые могут иметь причинное влияние на O. А также, если предположить, что сигналы не могут двигаться быстрее, чем скорость света, любое событие, например, например, B или C, в пространственноподобной области («где-то ещё»), не могут влиять на событие O, и они не могут быть затронуты влиянием события O. При этом предположении исключается любая причинно-следственная связь между событием O и любыми событиями в пространственноподобной области светового конуса.[11]
Относительность одновременности[править | править код]

Все наблюдатели согласятся, что для любого заданного события любое событие в световом конусе будущего (относительного заданного события) происходит после заданного события. Аналогично, для любого заданного события событие в световом конусе прошлого (относительно заданного события) происходит до заданного события. Отношение до-после, наблюдаемое для событий со времениподобным разделением, остаётся неизменным независимо от системы отсчёта наблюдателя, то есть независимо от движения наблюдателя. Ситуация совершенно отличается для пространственно-подобно разделённых событий. Рис.2-4 нарисован для системы отсчёта наблюдателя, движущегося с v = 0. В этой системе отсчёта событие C происходит после события O, и событие B происходит до события O. В другой системе отсчёта порядок этих событий, не связанных причинно, может быть обратным. В частности, если два события являются одновременными в конкретной системе отсчёта, они обязательно разделяются пространственноподобным интервалом и, следовательно, причинно не связаны друг с другом. То, что одновременность не является абсолютной, а зависит от системы отсчёта наблюдателя, называется относительность одновременности.[12]
На рис. 2-6 показано использование пространственно-временных диаграмм при анализе относительности одновременности. События в пространстве-времени являются инвариантными, но системы координат преобразуются, как обсуждалось выше для рис. 2-3. Три события (A, B, C) являются одновременными из системы отсчёта наблюдателя, движущегося со скоростью v = 0. Из системы отсчёта наблюдателя, движущегося со скоростью v = 0,3 c, события происходят в порядке C, B, A. Из системы отсчёта наблюдателя, движущегося со скоростью v = -0.5 c , события происходят в порядке A, B, C. Белая линия представляет собой плоскость одновременности, которая перемещается из прошлого наблюдателя в будущее наблюдателя, выделяя события, находящиеся на ней. Серая область — световой конус наблюдателя, который остаётся неизменным.
Пространственноподобный интервал пространства-времени даёт такое же расстояние, которое наблюдатель мог бы измерить, если измеряемые события были бы одновременными с ним. Таким образом, пространственноподобный интервал пространства-времени обеспечивает меру собственного расстояния, то есть истинного расстояния = Аналогично, времениподобный промежуток пространства-времени даёт такой же показатель времени, который будет представлен совокупным тиканием часов, которые перемещаются вдоль данной мировой линии. Таким образом, времениподобный интервал пространства-времени обеспечивает меру собственного времени = .[10]:220–221
Инвариантная гипербола[править | править код]

В евклидовом пространстве (имеющем только пространственные размеры) множество точек, эквидистантных (с использованием евклидовой метрики) из некоторой точки, образуют круг (в двух измерениях) или сферу (в трёх измерениях). В (1+1)-мерном пространстве-времени Минковского (имеющем одно временное и одно пространственное измерение) точки с постоянным пространственно-временным интервалом от начала координат (с использованием метрики Минковского) образуют кривые, задаваемые двумя уравнениями:
- где положительная действительная константа.
Эти уравнения описывают два семейства гипербол на пространственно-временной диаграмме x;ct, которые называются инвариантными гиперболами.
На рис. 2-7а каждая пурпурная гипербола соединяет все события, имеющие некоторое фиксированное пространственно-подобное отделение от начала координат, в то время как зелёные гиперболы связывают события с равным времениподобным разделением.
На рис. 2-7б показана ситуация в (1+2)-мерном пространстве-времени Минковского (одно временное и два пространственных измерения) с соответствующими гиперболоидами. Каждый времениподобный интервал образует однополостный гиперболоид, а каждый пространственно-подобный интервал образует двуполостный гиперболоид.
(1+2)-мерная граница между пространственно и времениподобными гиперболоидами, образуется событиями, имеющими нулевой интервал пространства-времени до начала координат, складывающимися при вырождении гиперболоидов в световой конус. В (1+1)-мерном пространстве Минковского гиперболы вырождаются в две серые линии с углами 45°, изображённые на рис. 2-7а.
Примечание по обозначениям: Пурпурные гиперболы, которые пересекают ось х, называются времениподобными (в отличие от пространственно-подобных) гипербол, потому что все «расстояния» до начала координат вдоль гипербол являются времениподобными интервалами. Из-за этого эти гиперболы представляют собой пути, которые могут иметь (постоянно ускоряющиеся) частицы в пространстве-времени: между любыми двумя событиями на одной гиперболе возможно отношение причинности, поскольку обратный наклон -представляющий необходимую скорость- для всех секущих меньше . С другой стороны, зелёные гиперболы, которые пересекают ось ct, называются пространственно-подобными, так как все интервалы вдоль этих гипербол являются пространственно-подобными интервалами: никакой причинности нет между любыми двумя точками на одной из этих гипербол, потому что все секущие представляют скорости, превышающие
Замедление времени и сокращение длин[править | править код]

На рис. 2-8 показана инвариантная гипербола для всех событий, которые могут быть достигнуты из начала координат за собственное время 5 метров (приблизительно 1,67⋅10−8 сек). Различные мировые линии представляют собой часы, движущиеся с разной скоростью. Часы, которые являются стационарными относительно наблюдателя, имеют вертикальную мировую линию, а время, измеренное наблюдателем, совпадает с собственным временем. Для часов, движущихся со скоростью 0.3c, время, измеренное наблюдателем, составляет 5,24 метра (1,75⋅10−8 сек), а для часов, движущихся со скоростью 0,7c , время, измеренное наблюдателем, составляет 7,00 метров (2,34⋅10−8 сек). Это иллюстрирует явление, известное как замедление времени. У часов, которые перемещаются быстрее, занимает больше времени (в системе отсчёта наблюдателя), чтобы отсчитать то же самое количество собственного времени, и они перемещаются дальше по оси x, чем они могли бы без замедления времени.[10]:220–221 Замедления времени двумя наблюдателями в разных инерциальных системах отсчёта — взаимны. Если наблюдатель O наблюдает часы наблюдателя O' как более медленные в своей системе отсчёта, наблюдатель O' в свою очередь, будет также наблюдать часы наблюдателя O как замедленные.

сокращение длины, подобно замедлению времени, является проявлением относительности одновременности. Измерение длины требует измерения интервала пространства-времени между двумя событиями, которые одновременно находятся в одной системе отсчёта. Но события, которые одновременно в одной системе отсчёта, в общем, не являются одновременными в других системах отсчёта.
На рис.2-9 показаны движения метрового стержня, движущегося со скоростью 0,5 c вдоль оси x. Края синей полосы представляют собой мировые линии двух крайних точек стержня. Инвариантная гипербола иллюстрирует события, отделённые от начала координат пространственноподобным интервалом в 1 м. Конечные точки O и B, измеренные при t' = 0, являются одновременными событиями в системе отсчёта S'. Но для наблюдателя в системе отсчёта S события O и B не являются одновременными. Чтобы измерить длину, наблюдатель в системе отсчёта S измеряет конечные точки стержня, проецируемого на ось x по их мировым линиям. Проекция «всемирного листа» стержня на ось x даёт укороченную длину OC.[4]:125
(не показано). Рисование вертикальной линии через А так, чтобы она пересекалось с осью х' , демонстрирует, что, даже когда ОВ укорочено с точки зрения наблюдателя О, ОА также укорочено с точки зрения наблюдателя O'. Точно так же, как каждый наблюдатель наблюдает часы другого как более медленные, каждый наблюдатель наблюдает линейки другого как укороченные.
Взаимное замедление времени и парадокс близнецов[править | править код]
Взаимное замедление времени[править | править код]
Взаимное замедление времени и сокращение длины имеют тенденцию запутывать новичков как бы своей противоречивой концепцией. Непонимание состоит в том, что если наблюдатель A наблюдает часы наблюдателя B замедленными, просто потому, что B движется со скоростью v по отношению к A, тогда принцип относительности требует, чтобы наблюдатель B также наблюдал часы A как замедленные. Это важный вопрос, который «лежит в основе понимания специальной теории относительности».[10]:198
В целом, A и B выполняют два разных измерения.
Чтобы измерить скорость тикания одних из часов B, A должен использовать двое своих собственных часов, первые для записи времени, когда часы B сначала отмечены в первом местоположении B, и вторые, чтобы записать время в другом местоположении B. Наблюдателю A требуется двое часов, потому что B движется, поэтому в измерениях задействовано всего трое часов. Двое часов A должны быть синхронизированы в системе отсчёта A. Напротив, B требует двух синхронизированных часов в своей системе отсчёта для записи показаний часов A в двух разных местах. Следовательно, A и B выполняют свои измерения с различными наборами из трёх показаний каждый. Поскольку они не выполняют измерение с одним набором часов, то нет необходимости в том, чтобы измерения были взаимно «согласованными», когда один наблюдатель наблюдал бы часы второго замедленными, а второй наблюдатель наблюдал бы ускоренные часы первого.[10]:198–199
Что касается сокращения взаимной длины, рис. 2-9 иллюстрирует, что собственные и несобственные системы отсчёта взаимно повёрнуты на гиперболический угол (аналогично обычным углам в евклидовой геометрии).[note 1] Из-за этого вращения проекция собственной метровой метки на не собственную ось x укорочена, а проекция несобственной метровой метки на собственную x'-ось также укорочена.

Рисунок 2-10 усиливает предыдущие рассуждения о взаимном замедлении времени. На этом рисунке события A и C отделены от события O равными времениподобными интервалами. Из несобственной системы отсчёта события A и B измеряются как одновременные, но для несобственного наблюдателя прошло больше времени, чем для собственного. В собственной системе отсчёта события C и D измеряются как одновременные, но для собственного наблюдателя прошло больше времени, чем для несобственного. Каждый наблюдатель измеряет часы другого наблюдателя как замедленные.[4]:124
Обратите внимание на важность слова «измерять». Состояние движения наблюдателя не может влиять на наблюдаемый объект, но оно может влиять на измерения объекта.
На рис.2-10 каждая линия, проходящая параллельно оси x, представляет собой линию одновременности для несобственного наблюдателя. Все события на этой линии имеют одинаковое значение времени ct. Аналогично, каждая линия, проведённая параллельно оси x' , представляет собой линию одновременности для собственного наблюдателя. Все события на этой линии имеют одинаковое значение времени ct' .
Парадокс близнецов[править | править код]
Элементарные введения в специальную теорию относительности часто иллюстрируют различия между галилеевой относительностью и специальной теорией относительности, создавая ряд предполагаемых «парадоксов». Все парадоксы в действительности представляют собой просто неправильные или непонятые проблемы, вызванные нашей незнакомостью со скоростями, сравнимыми со скоростью света. Выходом является решение многих задач в специальной теории относительности и ознакомление с её так называемыми контр-интуитивными предсказаниями. Геометрический подход к изучению пространства-времени считается одним из лучших методов развития современной интуиции.[13]
Парадокс близнецов — мысленный эксперимент, включающий идентичных близнецов, один из которых совершает путешествие в космос на скоростной ракете, возвращаясь домой, чтобы обнаружить, что близнец, который остался на Земле, постарел больше, чем он сам. Этот результат кажется странным, потому что каждый близнец наблюдает за другим близнецом как движущимся, и поэтому на первый взгляд кажется, что каждый должен обнаружить другого в более молодом возрасте. Парадокс близнецов уклоняется от обоснования взаимного замедления времени, представленного выше, избегая требования третьих часов.[10]:207 Тем не менее, «парадокс близнецов» не является истинным парадоксом, потому что его легко понять в контексте специальной теории относительности.
Такое впечатление, что парадокс существует из-за непонимания того, о чём говорит специальная теория относительности. Специальная теория относительности объявляет не все системы отсчёта эквивалентными, а только инерциальные. Система отсчёта движущегося близнеца не является инерционной в моменты, когда он ускоряется. Различие же между близнецами в наблюдаемом мире заключается во включении двигателей ракеты путешествующим близнецом, для того, чтобы вернуться домой, в то время как близнец-домосед ничего не делает.[14]

Необходим более глубокий анализ, прежде чем мы сможем понять, почему эти различия должны приводить к различию в возрасте близнецов. Рассмотрим диаграмму пространства-времени на рис. 2-11. Она представляет собой простой случай, когда близнец движется прямо по оси х и сразу поворачивает назад. С точки зрения близнеца-домоседа, нет ничего сложного в парадоксе близнецов. Собственное время, измеренное вдоль мировой линии путешествующего двойника от O до C, плюс собственное время, измеренное от C до B, меньше, чем собственное время пребывания близнеца, измеренное от O через A до B. Более сложные траектории требуют интегрирования собственного времени между соответствующими событиями вдоль кривой (то есть Криволинейный интеграл), чтобы вычислить общее количество времени, затрачиваемого путешествующим двойником.[14]
Осложнения возникают, если парадокс двойника анализируется с точки зрения движущегося двойника.
Для остальной части этого обсуждения мы принимаем номенклатуру Вайса, обозначающую близнеца-домоседа, как Теренс, и путешествующего близнеца, как Стелла[14].
Ранее мы отмечали, что Стелла не находится в инерциальной системе отсчёта. Учитывая этот факт, иногда утверждается, что полное разрешение двойного парадокса требует общей теории относительности. Это неверно[14].
Анализ с использованием только СТО был бы следующим: в системе отсчёта Стеллы она сама неподвижна в течение всего путешествия. Когда она активирует двигатели ракеты для разворота, она испытывает псевдосилу, которая похожа на гравитационную силу[14]. Рис. 2-6 и 2-11 иллюстрируют понятие линий (плоскостей) одновременности: линии, параллельные оси x наблюдателя (плоскости xy), представляют собой совокупности событий, которые одновременны в системе отсчёта этого наблюдателя. На рис. 2-11 синие линии соединяют события на мировой линии Теренца, которые с точки зрения Стеллы одновременны с событиями на её мировой линии. (Теренс, в свою очередь, будет наблюдать набор горизонтальных линий одновременности.) На протяжении как удаляющейся так и приближающейся частей пути Стеллы она измеряет часы Теренса как идущие более медленно, чем её собственные. Но во время поворота (то есть между жирными синими линиями на рисунке) происходит изменение угла её линий одновременности, что соответствует быстрому пропуску событий на мировой линии Теренса, которые Стелла считает одновременными с ней. Поэтому, по окончании поездки, Стелла считает, что Теренс имеет возраст больше, чем она[14].
Хотя общая теория относительности не требуется для анализа парадокса двойника, применение принципа эквивалентности общей теории относительности действительно даёт некоторое дополнительное представление о предмете. Ранее мы отмечали, что Стелла не неподвижна в инерциальной системе отсчёта. В своей покоящейся системе отсчёта Стелла неподвижна в течение всей поездки. Пока она движется равномерно, её система отсчёта становится инерциальной, и часы Теренса будут замедленными. Но когда она активирует двигатели ракеты для поворота, её система отсчёта является ускоренной, и она испытывает силу, которая толкает её так, как если бы она находилась в гравитационном поле. Теренс будет находится как бы на высоте в этом поле и из-за гравитационного замедления времени, его часы будут идти быстрее настолько, что в конечном результате Теренсу будет больше лет, чем Стелле, когда они снова встретятся[14]. Как будет обсуждаться далее, теоретические аргументы, предсказывающие гравитационное замедление времени, не являются исключительными для общей теории относительности. Любая теория гравитации будет предсказывать гравитационное замедление времени, если она соблюдает принцип эквивалентности, включая теорию Ньютона[10]:16.
Гравитация[править | править код]
В этом вводном разделе основное внимание было сосредоточено на пространстве-времени специальной теории относительности, поскольку она проще. Пространство времени Минковского плоское, не учитывает гравитацию, повсюду однородное и служит не более чем статическим фоном для событий, происходящих в нём. Наличие гравитации значительно усложняет описание пространства-времени. В общей теории относительности пространство-время больше не является статическим фоном, но активно взаимодействует с физическими системами, которые оно содержит. Кривизна пространства-времени в присутствии материи может распространять волны, изгибать путь света и проявляться во множество других явлений[10]:221 Некоторые из этих явлений описаны в последующих разделах этой статьи.
Основы математики пространства-времени[править | править код]
Преобразования Галилея[править | править код]

Основная цель состоит в том, чтобы иметь возможность сравнивать измерения, сделанные наблюдателями, которые находятся в движении относительно друг друга. Скажем, у нас есть наблюдатель O в системе отсчёта S, который измерил временные и пространственные координаты события, присвоив этому событию три декартовых координаты и время, измеренное на его решётке синхронизированных часов (x, y, z, t) (см. Рисунок 1-1). Второй наблюдатель O' в другой системе отсчёта S' измеряет то же самое событие в его системе координат и его решётке синхронизированных часов (x' , y' , z' , t' ). Поскольку мы имеем дело с инерциальными системами отсчёта, не один наблюдатель не находится под действием ускорения. Простой набор уравнений позволяет связать координаты (x, y, z, t) с (x' , y' , z' , t' ). Учитывая, что две системы координат находятся в стандартной конфигурации, что означает, что они выровнены параллельно координатам (x, y, z) и что t = 0, когда t' = 0, преобразование координат выглядит следующим образом:[15][16]
На рисунке 3-1 показано, что в теории Ньютона время является универсальным[17]:36-37. Рассмотрим следующий мысленный эксперимент: красная стрелка иллюстрирует поезд, который движется 0,4с относительно платформы. В поезде пассажир стреляет пулей со скоростью 0,4c в системе отсчёта поезда. Синяя стрелка иллюстрирует, что человек, стоящий на железнодорожных путях, измеряет скорость пули 0,8с. Это соответствует нашим наивным ожиданиям.
В более общем плане предположим, что система отсчёта S' движется со скоростью v относительно системы отсчёта S. В пределах системы S' наблюдатель O' измеряет объект, движущийся со скоростью u' . Какова его скорость u по отношению к системе S? Поскольку x = ut, x' = x − vt, и t = t' , мы можем написать x' = ut − vt = (u − v)t = (u − v)t' . Это приводит к u' = x' /t' и в конечном счёте
- или
которое является обычным галилеевым законом сложения скоростей.
Релятивистский закон сложения скоростей[править | править код]

Сложение скоростей в релятивистском пространстве-времени сильно отличается от классического. Чтобы немного уменьшить сложность уравнений, введём сокращение для отношения скорости объекта относительно скорости света,
На рисунке 3-2а показан красный поезд, который движется вперёд со скоростью, определяемой как v/c = β = s/a. В системе отсчёта поезда пассажир стреляет пулей со скоростью u' /c = β' = n/m, где расстояние измеряется вдоль линии, параллельной красной оси x' , а не чёрной x. Какова составная скорость u пули, представленная синей стрелкой, относительно платформы? Обращаясь к рис. 3-2b:
- С платформы составная скорость пули определяется как u = c(s + r)/(a + b).
- Два жёлтых треугольника подобны, потому что они являются прямоугольными треугольниками, которые имеют общий угол α. В большом жёлтом треугольнике отношение s/a = v/c = β.
- Соотношения соответствующих сторон двух жёлтых треугольников постоянны, так что r/a = b/s = n/m = β' . Тогда b = u' s/c и r = u' a/c.
- Подставим выражения для b и r в выражение для u в шаге 1, чтобы получить формулу Эйнштейна для сложения скоростей:[17]:42–48
Релятивистская формула для сложения скоростей, представленная выше, демонстрирует несколько важных свойств:
- Если u' и v очень малы по сравнению со скоростью света, то произведение vu' /c2 становится исчезающе малым, и общий результат становится неотличимым от формулы Галилея (формула Ньютона) для сложения скоростей: u = u' + v. Формула Галилея является частным случаем релятивистской формулы, применимой к малым скоростям.
- Если u' задано равным c, то формула даёт u = c независимо от стартового значения v. Скорость света одинакова для всех наблюдателей, независимо от их движения относительно источника излучения[17]:49.
Ещё раз про замедление времени и сокращение длин[править | править код]

Ранее мы качественно обсуждали замедление времени и сокращение длины. Для этих эффектов легко получить количественные выражения. Рис.3-3 представляет собой составное изображение, содержащее отдельные системы отсчёта, взятые из двух предыдущих анимаций, упрощённых и повторно обозначенных для целей настоящего раздела.
Чтобы немного уменьшить сложность уравнений, в литературе встречается множество различных сокращённых обозначений для ct :
- Общепринятые и .
- Также очень часто встречается использование соглашения

На рис.3-3а сегменты ОА и ОК представляют собой равные интервалы времени. Замедление времени представлено отношением OB/OK. Инвариантная гипербола имеет уравнение где k = OK, а красная строка, представляющая мировую линию частицы в движении имеет уравнение w = x/β = xc/v. Немного алгебраической преобразований дают
Выражение, содержащее символ квадратного корня, очень часто встречается в теории относительности, а единица делённая на выражение называется коэффициентом Лоренца, обозначаемым греческой буквой гамма :[18]
Заметим, что если v больше или равно c, выражение для становится физически бессмысленным, подразумевая, что c — максимально возможная скорость в природе. Далее отметим, что для любого v больше нуля коэффициент Лоренца будет больше одного, хотя форма кривой такова, что для низких скоростей коэффициент Лоренца очень близок к единице.
На рис.3-3b сегменты OA и OK представляют собой равные пространственно-временные интервалы. Сокращение длины представлено отношением OB/OK. Инвариантная гипербола умеет уравнение , где k = OK, и края синей полосы, представляющие мировые линии конечных точек стержня в движении, имеют наклон 1/β = c/v. Событие A имеет координаты (x, w) = (γk, γβk). Так как касательная линия через A и B имеет уравнение w = (x − OB)/β, получаем γβk = (γk − OB)/β и
Преобразования Лоренца[править | править код]
Галилеевские преобразования и их последовательный закон суммирования скоростей хорошо работают в нашем обычном низкоскоростном мире самолётов, автомобилей и шаров. Однако начиная с середины 1800-х годов чувствительная научная аппаратура начала обнаруживать аномалии, которые не соответствовали обычным прибавлениям скоростей.
В специальной теории относительности чтобы преобразовать координаты события из одной системы отсчёта в другую, мы используем преобразования Лоренца.
Прямые преобразования Лоренца:
Обратные преобразования Лоренца:
Когда v ≪ c и x достаточно мало, v2/c2 и vx/c2 стремятся к нулю, а преобразования Лоренца приближаются к преобразованиям Галилея.
Как отмечалось ранее, когда мы пишем и т. д., мы чаще всего действительно имеем в виду и т. д. Хотя для краткости мы пишем уравнения преобразования Лоренца без дельт, следует понимать, что х означает Δx и т. Д. Мы, как правило, всегда интересуемся промежутками пространства и времени между событиями.
Замечание об обозначениях: Названия одного набора преобразований прямыми преобразованиями Лоренца, а другой — обратными преобразованиями, может вводить в заблуждение, поскольку между системами отсчёта нет существенной разницы. Различные авторы называют обратными один или другой набор преобразований. Прямые и обратные преобразования тривиально связаны друг с другом, поскольку система отсчёта S может двигаться только вперёд или назад относительно S' . Поэтому инвертирование уравнений просто влечёт за собой переключение собственных и несобственных переменных и замену v на -v[19]:71–79.
Пример: Теренс и Стелла находятся на космической гонке «Земля-Марс». Теренс является официальным лицом на стартовой линии, а Стелла — участником. В момент времени t = t' = 0 космический корабль Стеллы мгновенно ускоряется со скоростью 0.5 c. Расстояние от Земли до Марса составляет 300 световых секунд (около 90,0⋅106 км). Теренс наблюдает, как Стелла пересекает часы финишной линии на t = 600.00 с. Но Стелла отмечает, что, когда она проходит финишную черту, время на хронометре её корабля t' = (t − vx/c2) = 519.62 с, и она получает расстояние между начальными и конечными линиями в своей системе отсчёта 259,81 световых секунд (около 77,9⋅106 км).
Вывод преобразований Лоренца[править | править код]

Было много десятков выводов преобразований Лоренца после оригинальной работы Эйнштейна в 1905 году, каждая из которых фокусировалась на чём то своём. Хотя вывод Эйнштейна основывался на неизменности скорости света, существуют и другие физические принципы, которые могут служить отправными точками для вывода преобразований. В конечном счёте, этими альтернативными отправными точками можно считать разные выражения лежащего в основе принципа локальности, в котором говорится, что влияние, которое одна частица оказывает на другое, не может передаваться мгновенно[20].
Вывод, приведённый здесь и проиллюстрированный на рис. 3-5, основан на одном из выводов представленных Байсом[17]:64–66 и использует предыдущие результаты из релятивистских сложения скоростей, замедления времени и сокращения длин. Событие P имеет координаты (w, x) в чёрной «системе покоя» и координаты (w' и x' ) в красной системе отсчёта, которая движется с параметром скорости β = v/c. Как мы определяем w' и x ' в терминах w и x? (Или наоборот)
Вначале легче получить обратное преобразование Лоренца.
- Начнём с того, что не может быть такого понятия, как увеличение/уменьшение длины в поперечных направлениях. y' должно равняться y, а z' должно быть равно z, в противном случае, возможность быстро движущемуся 1 м шарику пройти через 1 м круглое отверстие зависело бы от наблюдателя. В первом постулате относительности утверждается, что все инерциальные системы отсчёта эквивалентны, а поперечное увеличение/уменьшение нарушало бы этот закон[19]:27–28.
- Из рисунка, w = a + b и x = r + s
- Из предыдущих результатов, используя подобные треугольники, мы знаем, что s/a = b/r = v/c = β.
- Мы знаем, что из-за замедления времени, a = γw'
- Подставляя уравнение (4) в s/a = β получаем s = γw'β.
- Сокращение длины и подобные треугольники дают нам r = γx' и b = βr = βγx'
- Подставляя выражения для s, a, r and b в уравнения в шаге 2, сразу получаем
Вышеприведённые уравнения являются альтернативными выражениями для t и x уравнений обратного преобразования Лоренца, как видно из подстановки ct для w, ct' для W' и v/c для β. Из обратного преобразования уравнения прямого преобразования могут быть получены путём разрешения для t' и x' .
Линейность преобразований Лоренца[править | править код]
Преобразования Лоренца имеют математическое свойство, называемое линейностью, так как x' и t' получаются в виде линейных комбинаций x и t, без участия более высоких степеней. Линейность преобразования отражает фундаментальное свойство пространства-времени, которое мы молчаливо предполагали при выполнении вывода, а именно, что свойства инерциальных систем отсчёта не зависят от местоположения и времени. В отсутствие гравитации пространство-время выглядит везде одинаково[17]:67. Все инерциальные наблюдатели согласятся с тем, что представляет собой ускоренное и не ускоренное движение[19]:72–73. Любой наблюдатель может использовать собственные измерения пространства и времени, но в них нет ничего абсолютного[10]:190.
Результатом линейности является то, что если два преобразования Лоренца применяются последовательно, то результат также будет являться преобразованием Лоренца.
Пример: Теренс наблюдает, что Стелла улетает от него со скоростью 0,500 c, и он может использовать преобразования Лоренца с β = 0,500, чтобы связать свои измерения с измерениями Стеллы. Стелла в своей системе отсчёта наблюдает, как Урсула улетает от неё на скорости 0.250 c, и она может использовать преобразования Лоренца с β = 0,250, чтобы связать измерения Урсулы с её собственными. Из-за линейности преобразований и релятивистского сложения скоростей Теренс может использовать преобразования Лоренца с β = 0,666, чтобы связать измерения Урсулы с его собственным.
Эффект Доплера[править | править код]
Эффект Доплера — изменение частоты или длины волны для движущихся относительно друг друга источника и приёмника. Для простоты рассмотрим здесь два основных случая: (1) Движения источника и/или приёмника находятся точно вдоль линии, их соединяющей (продольный эффект Доплера), и (2) движения находятся под прямым углом к указанной линии (поперечный эффект Доплера). Мы игнорируем случаи, в которых они перемещаются по промежуточным углам.
Продольный эффект Доплера[править | править код]

Классический доплеровский анализ имеет дело с волнами, распространяющимися в среде, такими как звуковые волны или рябь воды, и которые передаются между источниками и приёмниками, когда они движутся в направлении или друг от друга. Анализ таких волн зависит от того, движутся ли источник, приёмник или оба относительно среды. Для случая, в котором приёмник является стационарным по отношению к среде, а источник удаляется непосредственно от приёмника со скоростью vs для параметра скорости βs, длина волны увеличивается, а наблюдаемая частота f задаётся формулой
С другой стороны, для случая, когда источник неподвижен, а приёмник движется прямо от источника со скоростью vr для параметра скорости βr, длина волны не изменяется, но скорость передачи волн относительно приёмника уменьшается, а наблюдаемая частота f задаётся выражением
Свет, в отличие от звуковой или водяной ряби, не распространяется через среду, и нет никакого различия между источником, удаляющимся от приёмника или приёмника, удаляющимся от источника. Рис.3-6 иллюстрирует релятивистскую пространственно-временную диаграмму, показывающую источник, отдаляющийся от приёмника с параметром скорости β, так что разделение между источником и приёмником в момент времени w равно βw. Из-за замедления времени w = γw' . Поскольку угловой коэффициент зелёного луча света равен −1,T = w+βw = γẃ(1+β). Следовательно, релятивистский эффект Доплера даётся выражением[17]:58–59
Поперечный эффект Доплера[править | править код]

Предположим, что источник, движущийся по прямой, находится в самой близкой точке к приёмнику. Казалось бы, классический анализ предсказывает, что приёмник не обнаруживает доплеровского сдвига. Из-за тонкостей в анализе это предположение не обязательно верно. Тем не менее, при соответствующем определении, поперечный доплеровский сдвиг является релятивистским эффектом, который не имеет классического аналога. Этими тонкостями являются следующие:[19]:94–96
- Рисунок 3-7а. Если источник, движущийся по прямой линии, пересекает поле зрения приёмника, каков результат измерение частоты, когда источник находится ближе всего к приёмнику?
- Рисунок 3-7b. Если источник движется по прямой линии, каков результат измерение частоты, когда приёмник видит источник в самом близком положении к нему?
- Рисунок 3-7с. Если приёмник движется по кругу вокруг источника, какую частоту измеряет приёмник?
- Рисунок 3-7d. Если источник перемещается по кругу вокруг приёмника, какую частоту измеряет приёмник?
В сценарии (a), когда источник ближе всего к приёмнику, свет, попадающий на приёмник, фактически идёт из направления, в котором источник был некоторое время назад, и имеет значительную продольную компоненту, усложняя анализ из системы отсчёта приёмника. Проще сделать анализ из S', системы отсчёта источника. Точка максимального приближения является независимой от системы отсчёта и представляет собой момент, когда нет никакого изменения расстояния со временем (то есть dr/dt = 0, где r — расстояние между приёмником и источником) и, следовательно, никакого продольного доплеровского сдвига. Источник наблюдает приёмник как освещённый светом частоты f' и имеющий замедленные часы. Следовательно в системе отсчёта S приёмник освещён светом, имеющим синее смещение
Сценарий (b) лучше всего анализировать из S, системы отсчёта приёмника. На рисунке показано, что приёмник освещён светом, когда источник был ближе всего к приёмнику, хотя источник уже переместился. Поскольку часы источника замедлены, и dr/dt в этот момент равно нулю, свет от источника, испущенный из этой ближайшей точки, имеет красное смещение
Сценарии (c) и (d) могут быть проанализированы с помощью простых аргументов замедления времени. В (c) приёмник наблюдает свет от источника как имеющий синее смещение с коэффициентом , а в (d) как имеющий красное смещение. Единственная кажущаяся сложность состоит в том, что объекты имеют орбитальное движение и, соответственно, имеют ускорения. Однако с точки зрения инерциального наблюдателя при вычислении замедления времени важна только мгновенная скорость часов. (Однако, обратное неверно.)[19]:94–96 Большинство сообщений о поперечном доплеровском сдвиге относятся к эффекту красного смещения и анализируют эффект с точки зрения сценариев (b) или (d)[note 2].
Энергия и импульс[править | править код]
Расширение импульса до четырёх измерений[править | править код]

В классической механике состояние движения частицы характеризуется её массой и её скоростью. Импульс, как произведение массы и скорости частицы, является векторной величиной, обладающей тем же направлением, что и скорость: p = mv. Это консервативная величина, что означает, что если на закрытую систему не влияют внешние силы, её полный линейный импульс не может измениться.
В релятивистской механике вектор импульса расширен до четырёх измерений. К вектору импульса добавляется компонента времени, которая позволяет вектору импульса пространства-времени преобразовываться подобно вектору положения (x, t) в пространства-времени. При изучении свойств импульса в пространстве-времени (см. рис. 3-8а) мы начинаем с рассмотрения частицы в состоянии покоя. В системе отсчёта покоя пространственная составляющая импульса равна нулю, то есть p = 0, но компонента времени равна mc.
Мы можем получить преобразованные компоненты этого вектора в движущейся системе отсчёта, используя преобразования Лоренца, или мы можем прочитать его непосредственно из рисунка, потому что мы знаем, (mc)́ = γmc и ṕ = −βγmc, так как красные оси масштабируются на коэффициент гамма. На рис. 3-8b показана ситуация в движущейся системе отсчёта. Очевидно, что пространственная и временная составляющие четырёхимпульса уходят в бесконечность при приближении скорости движущейся системы отсчёта к c[17]:84–87.
Мы будем использовать эту информацию в дальнейшем, чтобы получить выражение для четырёхимпульса.
Импульс света[править | править код]

Лёгкие частицы или фотоны движутся с постоянной скоростью c, которая известна как скорость света. Поэтому фотоны распространяются по светоподобной мировой линии и в соответствующих единицах имеют равные пространственные и временные составляющие для каждого наблюдателя.
Следствием уравнений Максвелла является то, что свет несёт энергию и импульс и что их отношение всегда постоянно: E/p = c. Или преобразовав E/c = p. Поскольку для фотонов пространственные и временные компоненты равны, значит, E/c следует отождествлять со временной составляющей вектора импульса в пространстве-времени.
Фотоны движутся со скоростью света, но имеют конечный импульс и энергию. Для этого массовый член в γmc должен быть равен нулю, что означает, что фотоны являются безмассовыми частицами. Бесконечность на ноль — некорректная величина, но E/c чётко определена.
В этом анализе, если энергия фотона равна E в системе отсчёта покоя, в движущейся системе координат она равна É = (1 − β)γE. Этот результат может быть получен путём исследования рис. 3-9 или путём применения преобразований Лоренца и согласуется с анализом эффекта Доплера, данным ранее[17]:88.
Взаимосвязь массы и энергии[править | править код]
Рассмотрение взаимосвязи между различными компонентами вектора релятивистского импульса привело Эйнштейна к нескольким известным выводам.
- В пределах низких скоростей, когда β = v/c приближается к нулю, приближается к 1, поэтому пространственная составляющая релятивистского импульса βγmc = γmv приближается к mv, то есть классическому импульсу. Следуя этому, γm можно интерпретировать как релятивистское обобщение m. Эйнштейн предположил, что релятивистская масса объекта увеличивается со скоростью по формуле mrel = γm.
- Аналогично, сравнивая временную составляющую релятивистского импульса с импульсом фотона, γmc = mrelc = E/c, Эйнштейн пришёл к взаимосвязи E = mrelc2. Упрощённый для случая нулевой скорости, это известное уравнение Эйнштейна, связывающее энергию и массу.
Другой способ взглянуть на соотношение между массой и энергией — рассмотреть серию разложений γmc2 при малых скоростях:
Второй член является просто выражением для кинетической энергии частицы. Масса действительно является другой формой энергии[17]:90–92[19]:129–130,180
Понятие релятивистской массы, введённое Эйнштейном в 1905 г., mrel, хотя и каждый день проверяется в ускорителях частиц по всему миру (или даже в любой аппаратуре, использование которой зависит от частиц имеющих высокие скорости, таких как электронные микроскопы,[21] старые цветные телевизоры и т. д.), тем не менее не доказано, что это плодотворная концепция в физике в том смысле, что она не является концепцией, которая послужила бы основой для другого теоретического развития. Релятивистская масса, например, не играет никакой роли в общей теории относительности.
По этой причине, как и для педагогических проблем, большинство физиков в настоящее время предпочитают другую терминологию, когда речь идёт о взаимосвязи между массой и энергией[22]. «Релятивистская масса» — устаревший термин. Термин «масса» сам по себе относится к массе покоя или инвариантной массе и равен инвариантной длине вектора релятивистского импульса. Выраженная в виде формулы,
Эта формула применима ко всем частицам, как безмассовым так и массивным. Для безмассовых фотонов она даёт ту же самую связь, которую мы ранее установили, E = ±pc[17]:90–92.
См. также: Окунь Л Б «Понятие массы (Масса, энергия, относительность)» УФН 158 511—530 (1989)
Четырёхимпульс[править | править код]
Из-за тесной взаимосвязи между массой и энергией, четырёхимпульс (также называемый 4-импульсом) часто называют 4-вектором энергии-импульса. Используя прописную букву Р для обозначения четырёхимпульса и строчную p для обозначения пространственного импульса, четырёхимпульс можно записать в виде
- или,
- используя соглашение [19]:129–130,180
Законы сохранения[править | править код]
В физике законы сохранения утверждают, что определённые измеримые свойства изолированной физической системы не меняются по мере развития системы со временем. В 1915 году Эмми Нётер обнаружила, что основой каждого закона сохранения является фундаментальная симметрия природы[23]. Тот факт, что физические процессы не волнует где они происходят в пространстве (Трансляционная симметрия), даёт закон сохранения импульса, тот факт, что такие процессы не волнует когда они происходят (трансляционная симметрия времени) даёт закон сохранения энергии, и так далее. В этом разделе мы рассмотрим ньютоновские взгляды на сохранение массы, импульса и энергии с релятивистской точки зрения.
Полный импульс[править | править код]

Чтобы понять, как необходимо изменить ньютоновский взгляд на сохранение импульса в релятивистском контексте, мы рассмотрим проблему двух сталкивающихся тел, ограниченных одним измерением.
В механике Ньютона можно выделить два крайних случая этой проблемы, которые дают математику минимальной сложности: (1) Два тела отскакивают друг от друга при полностью упругом столкновении. (2) Два тела склеиваются и продолжают двигаться как одна частица. Этот второй случай — случай полностью неупругого столкновения. Для обоих случаев (1) и (2) сохраняются импульс, масса и полная энергия. Однако кинетическая энергия не сохраняется в случаях неупругого столкновения. Определённая доля исходной кинетической энергии преобразуется в тепло.
В случае (2) две массы с импульсами p1 = m1v1 и p2 = m2v2 сталкиваются, чтобы создать единую частицу сохраняющейся массы m = m1 + m2, перемещающейся со скоростью центра масс исходной системы, vcm = (m1v1 + m2v2)/(m1 + m2). Полный импульс при этом сохраняется p = p1 + p2.
Рис. 3-10 иллюстрирует неупругое столкновение двух частиц с релятивистской точки зрения. Временные компоненты E1/c и E2/c суммируют до полного результирующего вектора E/c, что означает, что энергия сохраняется. Аналогично, пространственные компоненты p1 и p2 складываются в форму p результирующего вектора. Четырёхимпульсом, как и ожидалось, является сохраняющаяся величина. Однако инвариантная масса склеенной частицы, заданная точкой, где инвариантная гипербола полного импульса пересекает ось энергии, не равна сумме инвариантных масс отдельных частиц, которые столкнулись. Действительно, она больше суммы отдельных масс: m > m1 + m2[17]:94–97.
Рассматривая события этого сценария в обратной последовательности, мы видим, что несохранение массы является обычным явлением: когда неустойчивая элементарная частица спонтанно распадается на две более лёгкие частицы, полная энергия сохраняется, а масса нет. Часть массы преобразуется в кинетическую энергию[19]:134–138.
Выбор систем отсчёта[править | править код]
Свобода выбора любой системы отсчёта для проведения анализа позволяет выбрать ту, которая будет удобной. Для анализа задач с импульсами и энергией наиболее удобной системой отсчёта обычно является «система центра масс» (также называемый системой с нулевым импульсом или СЦМ-системой). Это система, в которой пространственная составляющая полного импульса системы равна нулю. Рис.3-11 иллюстрирует распад высокоскоростной частицы на две дочерние частицы. В лабораторной системе дочерние частицы предпочтительно излучаются в направлении, ориентированном вдоль траектории исходной частицы. Однако в системе СЦМ две дочерние частицы излучаются в противоположных направлениях, хотя их массы и величина их скоростей не одинаковы.
Сохранение энергии и импульса[править | править код]
В ньютоновском анализе взаимодействующих частиц преобразование между системами простое, потому что всё, что необходимо — применить преобразование Галилея ко всем скоростям. Так как v́ = v − u, то импульс ṕ = p − mu. Если общий импульс взаимодействующей системы частиц будет сохранён в одной системе, то также будет наблюдаться сохранение в любой другой системе[19]:241–245.
Сохранение импульса в системе СЦМ образует требование, что p = 0 как до, так и после столкновения. В ньютоновском анализе сохранение массы требует чтобы m = m1 + m2. В упрощённых одномерных сценариях, которые мы рассматривали, необходимо только одно дополнительное ограничение, прежде чем можно определить исходящие импульсы частиц — состояние энергии. В одномерном случае полностью упругого столкновения без потери кинетической энергии скорости частиц после столкновения в СЦМ-системе будут точно равными и противоположными по направлению. В случае полностью неупругого столкновения с полной потерей кинетической энергии скорости частиц после столкновения будут равны нулю[19]:241–245.
Ньютоновские импульсы, рассчитанные как p = mv, не могут корректно вести себя при преобразовании Лоренца. Линейное преобразование скоростей v́ = v − u заменяется сильно нелинейным v́ = (v − u)/(1 − vu/c2), так что вычисление, демонстрирующее сохранение импульса в одной системе отсчёта будет недействительным в других системах отсчёта. Перед Эйнштейном встал выбор либо отказаться от сохранения импульса, либо изменить определение импульса. Как мы видели в предыдущем разделе, он выбрал второй вариант и ввёл четырёхимпульс[17]:104.
Релятивистский закон сохранения энергии и импульса заменяет три классических закона сохранения энергии, импульса и массы. Масса больше не сохраняется, потому что она включена в общую релятивистскую энергию. Это делает релятивистское сохранение энергии более простым понятием, чем в нерелятивистской механике, поскольку полная энергия сохраняется без каких-либо уточнений. Кинетическая энергия, преобразованная в теплоту или внутреннюю потенциальную энергию, проявляется как увеличение массы[19]:127.
Пример: Из-за эквивалентности массы и энергии массы элементарных частиц обычно указаны в энергетических единицах, где 1 МэВ = 1 × 10 6 электрон-вольт. Заряженный пион представляет собой частицу с массой 139,57 МэВ (примерно в 273 раза больше массы электрона). Он неустойчив и распадается на мюон с массой 105,66 МэВ (примерно в 207 раз больше массы электрона) и антинейтрино, которое имеет пренебрежимо малую массу. Разница между массой пиона и массой мюона составляет 33,91 Мэв.
На рис. 3-12а показана диаграмма энергии-импульса для этой реакции распада в системе покоя пиона. Из-за своей незначительной массы нейтрино движется почти со скоростью света. Релятивистское выражение для его энергии, как и для фотона, есть Eν = pc,, которое также является значением пространственной составляющей его импульса. Чтобы сохранить импульс, мюон имеет то же значение пространственной составляющей импульса нейтрино, но в противоположном направлении.
В Интернете доступны алгебраические расчёты энергии распада этой реакции,[24], поэтому приведён рис. 3-12b. Энергия нейтрино равна 29,79 Мэв, а энергия мюона равна 33,91 - 29,79 = 4,12 МэВ. Большая часть энергии уносится нейтрино почти нулевой массы.
За пределами основ[править | править код]
Темы в этом разделе математически более сложные, чем те, которые были в предыдущих разделах, и не являются существенными для понимания Введения в искривлённое пространство-время.
Быстрота[править | править код]

Преобразования Лоренца связывают координаты событий в одной системе отсчёта с координатами в другой системе отсчёта. Для сложения двух скоростей используется релятивистский закон сложения скоростей, формулы которого нелинейны, что делает его более сложными, чем соответствующий закон Галилея.
Эта нелинейность является артефактом нашего выбора параметров[7]: 47-59. Ранее мы отмечали, что в пространственно-временной диаграмме x–ct, точки постоянного интервала от начала координат образуют инвариантную гиперболу. Мы также отмечали, что системы координат двух пространственно-временных систем отсчёта в стандартной конфигурации гиперболически повёрнуты относительно друг друга.
Естественными функциями для выражения этих соотношений являются гиперболические аналоги тригонометрических функций. На рис. 4-1а показана единичная окружность с sin (a) и cos (a), единственная разница между этой диаграммой и знакомой единичной окружности элементарной тригонометрии заключается в том, что a интерпретируется не как угол между лучом и осью x, а как двойная площадь сектора, заметаемая лучом от оси х. (Численно, угол и 2 × площади единичной окружности равны.) Рис. 4-1b показывает единичную гиперболу с sinh(a) и cosh(a), где a также интерпретируется как дважды окрашенная область.[25] На рис. 4-2 представлены графики функций sinh, cosh и tanh.
Для единичной окружности наклон луча определяется выражением
В прямоугольной системе координат, вращение точки (x, y) в точку (x́, ý) под углом θ определяется формулой
В пространственно-временной диаграмме параметр скорости является аналогом наклона (углового коэффициента). Быстрота φ определяется как[19]:96–99
где
Быстрота, определённая выше, очень полезна в специальной теории относительности, потому что многие выражения принимают более упрощённую форму, выраженную в её терминах. Например, быстрота просто аддитивна в коллинеарной формуле сложения скоростей[7]:47–59
или другими словами,
Преобразования Лоренца принимают простой вид, если выразить их в терминах быстроты. Фактор γ может быть записан как
Преобразования, описывающие относительное движение с равномерной скоростью и без вращения осей пространственных координат, называются бустами.
Подставляя γ и γβ в преобразования, которые были представлены ранее и переписаны в матричной форме, буст Лоренца в x направлении можно записать в виде
и обратный буст Лоренца в x направлении может быть записан как
Другими словами, буст Лоренца представляет гиперболическое вращение в пространстве-времени Минковского.[19]:96–99
Преимущества использования гиперболических функций таковы, что некоторые учебники, такие как классические Тейлор и Уилер, вводят их использование на очень ранней стадии[7][26][note 3]
4-векторы[править | править код]
4-вектора были упомянуты выше в контексте 4-вектора энергии-импульса. В целом ни один из элементарных выводов специальной теории относительности их не требует. Но однажды понятое понятие 4-вектора и более общее понятие тензора значительно упрощают математику и концептуальное понимание специальной теории относительности. Работа исключительно с такими объектами приводит к формулам, которые явно релятивистски инвариантны, что является значительным преимуществом в нетривиальных контекстах. Например, демонстрация релятивистской инвариантности уравнений Максвелла в их обычной форме не является тривиальной, а использование тензора электромагнитного поля превращает их в просто рутинный расчёт. С другой стороны, общая теория относительности с самого начала опирается в основном на 4-векторы и тензоры, представляющие физически релевантные сущности. Связь этих уравнений с помощью уравнений, не зависящих от конкретных координат, требует тензоров, способных связывать такие 4-векторы даже в искривлённом пространстве-времени, а не только в плоском как в специальной теории относительности. Изучение тензоров выходит за рамки этой статьи, в которой даётся лишь основное обсуждение пространства-времени.
Определение 4-вектора[править | править код]
Набор четырёх чисел A = (A0, A1, A2, A3) называется «4-вектором» если эти компоненты A i преобразуются между системами отсчёта согласно преобразованиям лоренца. При использовании (ct, x, y, z) координат, A является 4–вектором если A преобразуется (в направлении x) согласно
которое образуется от простой замены ct на A0 и x на A1 в более ранней версии преобразований лоренца.
Как обычно, когда мы пишем x, t и т. д., мы обычно имеем в виду Δx, Δt и т. д.
Последние три компоненты 4-вектора должны быть стандартным вектором в трёхмерном пространстве. Следовательно, 4-вектор должен преобразовываться как (c Δt, Δx, Δy, Δz) при преобразованиях Лоренца и при вращении.[13]:36–59
Свойства 4-векторов[править | править код]
- Замкнутость линейной комбинации: Если A и B являются 4-векторами, то C = aA + aB также является 4-вектором.
- Инвариантность скалярного произведения: Если A и B являются 4-векторами, то их скалярное произведение инвариантно, то есть не зависит от системы отсчёта, в которой оно рассчитано. Обратите внимание, как вычисление скалярного произведения отличается от вычисления скалярного произведения 3-вектора. Примем, что и являются 3-векторами:
- Помимо инвариантности преобразования Лоренца, указанное выше скалярное произведение также инвариантно относительно вращения в 3-пространстве.
- Два вектора называются ортогональными, если В отличие от случая 3-векторов ортогональные 4-векторы не обязательно находятся под прямым углом друг к другу. Два 4-вектора ортогональны, если они смещены на равные и противоположные углы от линии 45°, которая является мировой линией светового луча. Это означает, что светоподобный 4-вектор ортогонален сам себе.
- Инвариантность величины вектора: Величина вектора является скалярным произведением 4-вектора с самим собой и является независимым от системы отсчёта свойством. Как и с интервалами, величина может быть положительной, отрицательной или нулевой, так что векторы называются времениподобными, пространственно-подобными или светоподобными. Заметим, что светоподобный вектор не совпадает с нулевым вектором. Светоподобный вектор — тот, для которого , а нулевой вектор — тот, компоненты которого равны нулю. Особые случаи, иллюстрирующие инвариантность нормы, включают в себя инвариантный интервал и инвариантную длину вектора релятивистского импульса [19]:178–181[13]:36–59
Примеры 4-векторов[править | править код]
- 4-вектор смещения: Также имеет название разделение пространства-времени, это (Δt, Δx, Δy, Δz), или для бесконечно малых, (dt, dx, dy, dz).
- 4-вектор скорости: Этот вектор получается при делении 4-вектора смещения на , где — собственное время между двумя событиями, которые разделены dt, dx, dy и dz .
- Вектор 4-скорости касается мировой линии частицы и имеет длину, равную одной единице времени в системе отсчёта частицы.
- У ускоренной частицы нет инерциальной системы отсчёта, в которой она всегда находится в состоянии покоя. Однако, как указывалось ранее в более раннем обсуждении поперечного эффекта Доплера, всегда можно найти инерциальную систему отсчёта, которая мгновенно сопутствует частице. Такая мгновенно сопутствующая инерциальная система отсчёта (МСИСО) позволяет применять специальную теорию относительности для анализа ускоренных частиц.
- Поскольку фотоны движутся по светоподобным линиям, то для них и 4-скорость не может быть определена. Нет системы отсчёта, в которой фотон находится в состоянии покоя, и вдоль пути фотона невозможно найти МСИСО.
- 4-вектор энергии-импульса: Как обсуждалось в параграфе Энергия и импульс,
- Как указывалось ранее, существуют различные способы представления 4-вектора энергии-импульса. Его можно выразить как или Первая компонента — полная энергия (включая массу) частицы (или системы частиц) в данной системе отсчёта, а остальные компоненты — её пространственный импульс. 4-вектор энергии-импульса является сохраняющейся величиной.
- 4-вектор ускорения: Это результат взятия производной от 4-вектора скорости по
- '4-вектор силы:' Это производная от 4-вектора импульса по
Как и ожидалось, конечные компоненты вышеперечисленных 4-векторов являются стандартными 3-векторами, соответствующими пространственному 3-импульсу, 3-силе и т. д.[19]:178–181[13]:36–59
4-векторы и физические законы[править | править код]
Первый постулат специальной теории относительности объявляет эквивалентность всех инерциальных систем отсчёта. Физический закон, работающий в одной системе отсчёта должен продолжать работать во всех системах отсчёта, поскольку в противном случае мы могли бы различать эти системы отсчёта. Как отмечалось в предыдущем обсуждении сохранения энергии и импульса, ньютоновские импульсы не могут корректно вести себя при преобразовании Лоренца, и Эйнштейн предпочёл изменить определение импульса на один, связанный с 4-векторами, вместо того, чтобы отказаться от сохранения импульса.
Физические законы должны основываться на конструкциях, которые независимы от систем отсчёта. Это означает, что физические законы могут принимать форму уравнений, связывающих скаляры, которые всегда независимы от систем отсчёта. Однако уравнения, содержащие 4-векторы, требуют использования тензоров с соответствующим рангом, которые сами можно считать построенными из 4-векторов.[19]:186
Ускорение[править | править код]
Распространённым[у кого?] заблуждением является то, что специальная теория относительности применима только к инерционным системам отсчёта и что она не способна работать с ускоряющимися объектами или ускоренными системами отсчёта. Ускоряющиеся объекты обычно можно анализировать без необходимости иметь дело с ускоренными системами отсчёта в принципе. Общая теория относительности требуется только для сильных гравитационных полей.[27]
Однако корректная работа с ускоренными системами отсчёта требует некоторой осторожности. Разница между специальной и общей относительностью состоит в том, что (1) В специальной теории относительности все скорости относительны, но ускорение является абсолютным. (2) В общей теории относительности все виды движения относительны, и инерционное, и ускоренное, и вращение. Чтобы учесть эту разницу, общая теория относительности использует искривлённое пространство-время.[27]
В этом разделе мы проанализируем несколько сценариев, связанных с ускоренными системами отсчёта.
Парадокс Белла[править | править код]
Парадокс космического корабля Белла — хороший пример проблемы, когда интуитивное рассуждение, не связанное с геометрическим пониманием подхода пространства-времени, может привести к проблемам.

На рис.4-4 два одинаковых космических корабля висят в пространстве и находятся в покое относительно друг друга. Они соединены верёвкой, которая имеет ограничение на растяжение до разрыва. В данный момент в нашей системе отсчёта, системе отсчёта наблюдателя, оба космических корабля ускоряются в одном направлении вдоль линии между ними с одинаковым постоянным собственным ускорением[note 4] Вопрос — разорвётся ли верёвка?
Основная статья рассказывает о том, что, когда парадокс был новым и малоизученным, даже у профессиональных физиков возникли трудности с нахождением решения. Две линии рассуждений приводят к противоположным выводам. Есть два аргумента, которые представлены ниже, один из них ошибочен, несмотря на то, что даёт правильный ответ.[19]:106,120–122
- Для наблюдателя находящегося в покоящейся системе отсчёта, космические корабли начинают движение с дистанции L между ними и остаются на одном и том же расстоянии друг от друга во время ускорения. Во время ускорения L является укороченной длиной от длины Ĺ = γL в системах ускоряющихся космических кораблей. Спустя достаточно длительное время γ увеличится настолько, что верёвка должна разорваться.
- Пусть А и В будут задним и передним космическими кораблями. В системах отсчёта космических кораблей каждый космический корабль видит, что другой космический корабль делает то же самое, что и он. A говорит, что B имеет такое же ускорение, что и у него, и B видит, что A копирует каждое его движение. Таким образом, космические корабли остаются на одном и том же расстоянии друг от друга, и верёвка остаётся целой.[19]:106,120–122
Проблема с первым объяснением заключается в том, что нет системы отсчёта космических кораблей. Такой не может быть, потому что два космических корабля измеряют растущее расстояние между ними. Поскольку нет единой системы отсчёта космических кораблей, длина верёвки не определена. Тем не менее, вывод верен, и объяснение в основном правильное. А вот второе объяснение совершенно игнорирует относительность одновременности.[19]:106,120–122

Решение этого парадокса становится очевидным, если использовать пространственно-временную диаграмму (рис. 4-5). Два наблюдателя в пространстве-времени Минковского ускоряются с постоянной величиной ускорения за собственное время (ускорение и прошедшее время измеряются самими наблюдателями, а не сторонним инерциальным наблюдателем). Они являются сопутствующими и инерциальными до и после фазы ускорения. Как отметил Белл, в геометрии Минковского длина пространственноподобного отрезка A′B″ "оказывается больше длины пространственноподобного отрезка AB.
Увеличение длины можно рассчитать с помощью преобразования Лоренца. Если, как показано на рис. 4-5, ускорение закончено, корабли останутся с постоянным смещением в некоторой системе отсчёта Если и — позиции кораблей в то позиции в системе отсчёта :[28]
«Парадокс» как бы исходит из того, как Белл построил свой пример. В обычном обсуждении сокращений Лоренца покоящаяся линейка фиксирована, а движущаяся линейка сокращается измерениям в системе отсчёта . Как показано на рис.4-4, пример Белла вводит движущиеся длины и , измеренные в системе отсчёта как фиксированные, тем самым увеличивая покоящуюся длину в системе отсчёта .
Ускоренный наблюдатель с горизонтом[править | править код]
Некоторые специальные задачи по теории относительности могут привести к пониманию вещей, обычно связанных с общей теорией относительности. Это, например, горизонт событий. В тексте, сопровождающем рис. 2-7 в разделе инвариантная гипербола, мы отметили, что пурпурные гиперболы представляют собой реальные пути, которые проходит постоянно ускоряющийся путешественник в пространстве-времени. В периоды положительного ускорения скорость движения приближается к скорости света, в то время как в нашей системе отсчёта ускорение путешественника постоянно уменьшается.

На рис.4-6 подробно описаны различные особенности движений путешественника. В любой момент его пространственная ось образована линией, проходящей через начало координат и его текущее положение на гиперболе, а его ось времени является касательной к гиперболе в его местоположении. Параметр скорости приближается в пределе единице с ростом . Аналогично, приближается к бесконечности.
Форма инвариантной гиперболы соответствует пути постоянного собственного ускорения. Это можно показать следующим образом:
- Мы знаем что
- Так как заключаем, что
- С точки зрения релятивистского закона силы,
- Подставляя из шага 2 и выражения для из шага 3 получаем , которая является постоянным выражением.[17]:110–113
На рис.4-6 иллюстрируется конкретный расчётный сценарий. Теренс (A) и Стелла (B) первоначально стоят вместе в 100 световых часах от начала координат. Стелла взлетает в момент 0, её космический корабль ускоряется со скоростью 0.01 c в час. Каждые двадцать часов Теренс по радио сообщает Стелле о ситуации дома (сплошные зелёные линии). Стелла получает эти регулярные передачи, но возрастающее расстояние (частично компенсируемое замедлением времени) заставляет её получать сообщения Теренса позже и позже, согласно её часам, и она никогда не получает никаких сообщений от Теренса после 100 часов по его часам (пунктирные зелёные линии).[17]:110–113
Через 100 часов по часам Теренса Стелла входит в тёмную область. Она путешествовала за пределами времениподобного будущего Теренса. С другой стороны, Теренс может бесконечно продолжать получать сообщения Стеллы. Ему просто нужно подождать достаточно долго. Пространство-время было разделено на отдельные регионы кажущимся горизонтом событий. Пока Стелла продолжает ускоряться, она не может узнать, что происходит за этим горизонтом[17]:110–113
Введение в искривлённое пространство-время[править | править код]
Основные положения[править | править код]

Теории Ньютона предполагали, что движение происходит на фоне жёсткой евклидовой системы отсчёта, которая распространяется во всем пространстве и во все времена. Гравитация опосредована таинственной силой, действующей мгновенно на расстоянии, действия которой не зависят от промежуточного пространства.[note 5] Эйнштейн отрицал, что существует какая-либо фоновая евклидова система отсчёта, которая распространяется во всем пространстве. Также как нет такой вещи, как сила тяготения, а есть только структура самого пространства-времени.[7]:175–190
В пространстве-времени путь спутника, вращающегося вокруг Земли, не продиктован отдалёнными влияниями Земли, Луны и Солнца. Вместо этого спутник перемещается в пространстве только под влиянием локальных условий. Поскольку пространство-время везде локально плоское, если рассматривать его в достаточно малом масштабе, спутник всегда следует по прямой в своей локальной инерциальной системе координат. Мы говорим, что спутник всегда следует по пути геодезической. Гравитацию нельзя обнаружить рядом с движениями только одной частицы.[7]:175–190
При любом анализе пространства-времени для доказательства гравитации требуется наблюдения относительных ускорений двух тел или двух отдельных частиц. На рис. 5-1 две разделённые частицы, свободно падающие в гравитационном поле Земли, проявляют приливные ускорения из-за локальных неоднородностей в гравитационном поле, так что каждая частица идёт по другому пути через пространство-время. Приливные ускорения, которые эти частицы проявляют относительно друг друга, не требуют сил для их объяснения. Скорее, Эйнштейн описал их в терминах геометрии пространства-времени, то есть кривизны пространства-времени. Эти приливные ускорения строго локальны. Это совокупный общий эффект многих локальных проявлений кривизны, которые приводят к появлению гравитационной силы, действующей на большом расстоянии от Земли.[7]:175–190
В основе общей теории относительности лежат два основных положения.

- Первым важным понятием является координатная независимость: законы физики не могут зависеть от того, какую систему координат использовать. Это важное расширение принципа относительности по сравнению с версией, используемой в специальной теории относительности, в которой говорится, что законы физики должны быть одинаковыми для каждого наблюдателя, движущегося в неускоренных (инерциальных) системах отсчёта. В общей теории относительности, чтобы использовать собственные (переведённые) слова Эйнштейна, «законы физики должны быть такого характера, что они применимы к системам отсчёта в любом виде движения.»[29]:113Это приводит к проблеме: в ускоренных системах отсчёта ощущается сила, которая, позволит обнаружить наличие ускорения в абсолютном смысле. Эйнштейн разрешил эту проблему при помощи принципа эквивалентности.[30]:137–149
- Принцип эквивалентности утверждает, что в любой достаточно малой области пространства эффекты гравитации не отличаются от ускорения.
- На рисунке 5-2 человек A находится в космическом корабле, вдали от любых массивных объектов, который подвергается равномерному ускорению g. Человек B находится в ящике, покоящемся на Земле. При условии, что космический корабль достаточно мал, так что приливные эффекты не поддаются измерению (учитывая чувствительность прибора измерения силы тяжести, A и B предположительно должны быть лилипутами), не существует экспериментов, которые могли бы выполнять A и B и которые позволили бы им определить, в чём они находятся.[30]:141–149
- Альтернативное формулирование принципа эквивалентности состоит в том, что в универсальном законе тяготения Ньютона F = GMmg /r2 = mgg и во втором законе Ньютона F = m ia, нет причины априори, почему гравитационная масса mg должна быть равна инерционной массе m i. Принцип эквивалентности утверждает, что эти две массы идентичны.[30]:141–149
Чтобы перейти от элементарного описания искривлённого пространства-времени выше к полному описанию гравитации, требуется тензорное исчисление и дифференциальная геометрия, которые требуют серьёзного изучения. Без этих математических инструментов можно написать об общей теории относительности, но невозможно продемонстрировать какие-либо нетривиальные выводы.
Вместо попытки предложить (ещё одно) относительно не математическое представление об общей теории относительности, читателю предлагается перейти на уже опубликованные статьи Введение в общую теорию относительности и Общая теория относительности.
В этом разделе основное внимание будет уделено изучению нескольких элементарных случаев, которые служат для поверхностного знакомства с общей теории относительности.
Кривизна времени[править | править код]

В обсуждении специальной теории относительности силы играли второстепенную роль. Специальная теория относительности предполагает возможность задавать инерциальные системы отсчёта, которые заполняют всё пространство-время, и все часы которых идут в одинаковом темпе с часами в начале координат. Действительно ли возможно? В неоднородном гравитационном поле эксперимент говорит — нет. Гравитационные поля не позволяют построить глобальную инерциальную систему отсчёта. В достаточно малых областях пространства-времени всё ещё возможны локальные инерциальные системы отсчёта. Общая теория относительности включает в себя систематическое сшивание этих локальных систем отсчёта в более общую картину пространства-времени.[13]:118–126
Вскоре после публикации общей теории относительности в 1916 году ряд учёных указал, что общая теория относительности предсказывает существование гравитационного красного смещения. Сам Эйнштейн предложил следующий мысленный эксперимент: (i) Предположим, что была построена башня высоты h (рис. 5-3). (ii) Бросим частицу с массой покоя m с верхней части башни. Она свободно падает с ускорением g, достигая земли со скоростью v = (2gh)1/2, её полная энергия E, измеренная наблюдателем на земле, равна m + ½mv2/c2 = m + mgh/c2. (iii) Преобразователь массы-энергии преобразует полную энергию частицы в один высокоэнергетический фотон, который он направляет вверх. (iv) В верхней части башни преобразователь энергии-массы преобразует энергию фотона É обратно в частицу массы покоя ḿ.[13]:118–126
В результате должно быть m = ḿ, иначе можно было бы построить вечный двигатель. Поэтому мы прогнозируем, что É = m, так что
При подъёме в гравитационном поле Земли фотон теряет энергию, получая красное смещение. Ранние попытки измерить это красное смещение с помощью астрономических наблюдений были несколько неубедительными, но окончательные лабораторные наблюдения были выполнены в эксперименте Паунда и Ребки (1959), а позже — Паунда и Шнайдера (1964).[31]
Свет имеет соответствующую частоту, и эта частота может использоваться для управления работой часов. Гравитационное красное смещение приводит к важному выводу о времени: гравитация замедляет время. Предположим, мы построим двое одинаковых часов, чьи скорости контролируются некоторым стабильным атомным переходом. Поместим одни часы наверху башни, в то время как другие часы оставим на земле. Экспериментатор на верху башни регистрирует сигналы от наземных часов как имеющие более низкую частоту, чем сигналы часов рядом с ним на башне. Свет, поднимающийся на башню, — просто волна, и невозможно, чтобы гребни волн исчезли по пути вверх. Число осцилляции света, поступающих в верхнюю часть башни, равно числу, испускаемому внизу. Экспериментатор приходит к выводу, что наземные часы идут медленнее, и это можно подтвердить, спустив часы с башни, чтобы сравнить рядом с наземными часами.[10]:16-18 Для башни 1 км разница будет составлять около 9,4 наносекунды в день, легко измеримая с помощью современной аппаратуры.
Часы в гравитационном поле не идут с одинаковой скоростью. Эксперименты, такие как эксперимент Паунда-Ребки, уверенно установили кривизну временной составляющей пространства-времени. Эксперимент Паунда-Ребки ничего не говорит о кривизне пространственного компонента пространства-времени. Но учтите, что теоретические аргументы, предсказывающие гравитационное замедление времени, вообще не зависят от аргументов общей теории относительности. Любая теория гравитации будет предсказывать гравитационное замедление времени, если она соблюдает принцип эквивалентности.[10]:16 Включая ньютоновскую гравитацию. В общей теории относительности легко показывается как в Ньютоновском пределе (то есть когда частицы движутся медленно, гравитационное поле слабое и статичное), кривизны одного времени достаточно для получения Закон тяготения Ньютона.[32]:101–106
Ньютоновская гравитация — теория искривлённого времени. Общая теория относительности — теория искривлённого времени и искривлённого пространства. Полагая G как гравитационную постоянную, M как массу ньютоновской звезды и орбитальные тела с незначительной массой на расстоянии r от звезды, в пространственно-временном интервале для ньютоновской гравитации переменным является только коэффициент времени:[10]:229-232
Кривизна пространства[править | править код]
Коэффициент перед описывает кривизну времени в ньютоновской гравитации, и эта кривизна полностью учитывает все ньютоновские гравитационные эффекты. Как и ожидалось, этот поправочный коэффициент прямо пропорционален и , а из-за в знаменателе поправочный коэффициент увеличивается по мере приближения к гравитирующему телу, что означает искривление времени.
Но общая теория относительности — теория искривлённого пространства и искривлённого времени, поэтому, если существуют члены, изменяющие пространственные компоненты интервала пространства-времени, представленного выше, не следует ли рассматривать эффекты на планетарных и спутниковых орбитах как результат коэффициентов кривизны, стоящих у пространственных членов?
Ответ заключается в том, что они видны, но эффекты крошечные. Причина в том, что скорости планет чрезвычайно малы по сравнению со скоростью света, так что для планет и спутников солнечной системы член перекрывает пространственные члены.[10]:234-238
Несмотря на малость пространственных членов, первые признаки того, что что-то было не так с ньютоновской гравитацией, были обнаружены полтора века назад. В 1859 году Урбен Леверье в анализе доступных временных наблюдений за смещениями Меркурия над диском Солнца с 1697 по 1848 год сообщил, что известная физика не может объяснить орбиту Меркурия, кроме как допустить существование на орбите Меркурия другой планеты или пояса астероидов. Перигелий орбиты Меркурия показал наличие избыточной скорости прецессии по сравнению с тем, что может быть объяснено влиянием других планет.[33] Возможность обнаруживать и точно измерять минутное значение этой аномальной прецессии (всего 43 угловых секунды за тропический год) является свидетельством большой точности астрометрии XIX века.

Как и знаменитый астроном, который когда-то обнаружил существование Нептуна «на кончике пера», анализируя колебания орбите Урана, объявление Леверье вызвало двухлетний период «Вулканомании», когда астрономы-профессионалы и астрономы-любители охотились за гипотетической новой планетой. Этот поиск включал несколько ложных наблюдений Вулкана. В конечном итоге было установлено, что никакой планеты или пояса астероидов не существует[34].
В 1916 году Эйнштейн наконец показал, что эта аномальная прецессия Меркурия объясняется пространственными членами в кривизне пространства-времени. Кривизна во временном члене, будучи просто выражением ньютоновской тяготения, не имеет никакого отношения к объяснению этой аномальной прецессии. Успех его расчёта был мощным показателем для сверстников Эйнштейна, что общая теория относительности может быть верной.
Наиболее впечатляющим из предсказаний Эйнштейна был расчёт того, что члены кривизны в пространственных компонентах интервала пространства-времени могут быть измерены при изгибе света около массивного тела. Свет имеет наклон ±1 на диаграмме пространства-времени. Его движение в пространстве равно его движению во времени. Для выражения слабого поля инвариантного интервала Эйнштейн рассчитал точно равную, но противоположную по знаку кривизну в пространственных компонентах.[10]:234–238
В гравитации Ньютона коэффициент перед предсказывает изгиб света вокруг звезды. В общей теории относительности коэффициент перед предсказывает изгиб вдвое больший.[10]:234–238
Историю наблюдения Эддингтона 1919 года и затмения Эйнштейна можно изучить в дополнительном источнике.[35]
Источники кривизны пространства-времени[править | править код]

energy density - плотность энергии; momentum density - плотность импульса; momentum flux - поток импульса; shear stress - сдвиговое напряжение; pressure - давление.
В законе всемирного тяготения Ньютона единственным источником гравитационной силы является масса.
Общая теория относительности указывает несколько источников кривизны пространства-времени в дополнение к массе. В уравнениях поля Эйнштейна, источники силы тяжести представлены в правой части в the тензора энергии-импульса.
На рис. 5-5 классифицируются различные источники силы тяжести в тензоре энергии напряжений:
- (красный): полная плотность массы, включая любые вклады в потенциальную энергию от сил между частицами, а также кинетическую энергию от случайных тепловых движений.
- and (оранжевый): это коэффициенты плотности импульса. Даже если движение масс отсутствует, энергия может передаваться теплопроводностью, и энергия проводимости будет иметь импульс.
- — скорости потока i-компоненты импульса на единицу площади в J-направлении. Даже если нет движения массы, случайные тепловые движения частиц будут приводить к импульсному потоку, поэтому компоненты i = j (зелёный) представляют изотропное давление, а компоненты i ≠ j (синие) представляют собой сдвиговые напряжения.[36]
Из уравнений можно сделать один важный вывод, который на разговорном языке можно назвать как гравитация сама создаёт гравитацию.[note 6] Энергия имеет массу. Даже в ньютоновской гравитации гравитационное поле связано с энергией, E = mgh,, называемой гравитационной потенциальной энергией. В общей теории относительности энергия гравитационного поля возвращается к созданию гравитационного поля. Это делает уравнения нелинейными и трудными для решения во всех случаях, кроме случая слабого поля.[10]:240 Численная относительность является ветвью общей теории относительности и использует численные методы с привлечением суперкомпьютеров для изучения чёрных дыр, гравитационных волн, нейтронных звёзд и других явлений с сильными полями.
Энергия-импульс[править | править код]
(справа) Вращающееся распределение массы-энергии с моментом импульса J генерирует гравитомагнитное поле H
В специальной теории относительности масса-энергия тесно связана с импульсом. Как мы уже обсуждали ранее в разделе Энергия и импульс, так же, как пространство и время являются разными аспектами более всеобъемлющего объекта, называемого пространством-временем, масса-энергия и импульс просто разные аспекты единой, четырёхмерной величины, называемой четырёхимпульс. Следовательно, если масса-энергия является источником силы тяжести, импульс также должен быть таким источником. Включение импульса в качестве источника силы тяжести приводит к предсказанию того, что движущиеся или вращающиеся массы могут генерировать поля, аналогичные магнитным полям, генерируемым движущимися зарядами, явление, известное как гравитомагнетизм.[37]

Хорошо известно, что сила магнетизма может быть выведена путём применения правил специальной теории относительности к движущимся зарядам. (Красноречивая демонстрация этого была представлена Фейнманом в томе II, глава 13-6 его Лекций по физике, доступных онлайн.[38]) Аналогичную логику можно использовать для доказательства происхождения гравитомагнетизма. На рис.5-7а два параллельных бесконечно длинных потока массивных частиц имеют равные и противоположные скорости -v и +v относительно неподвижной пробной частицы, центрированной между ними. Из-за симметрии установки общая сила на центральную частицу равна нулю. Предположим, что v << c, так что скорости просто суммируются. На рис.5-7b показана точно такая же установка, но в системе отсчёта верхнего потока. Пробная частица имеет скорость +v, а нижний поток имеет скорость +2v. Поскольку физически ситуация не изменилась, а изменилась только система отсчёта, в которой мы наблюдаем за экспериментом, пробная частица не должна притягиваться ни к одному из потоков. Но не очевидно, что силы, действующие на пробную частицу, равны. (1) Поскольку нижний поток движется быстрее верхнего, каждая частица в нижнем потоке имеет большую массу-энергию, чем частица в верхнем. (2) Из-за сокращения Лоренца в нижнем потоке больше частиц на единицу длины, чем в верхнем потоке. (3) Ещё один вклад в активную гравитационную массу нижнего потока исходит из дополнительного члена давления, для обсуждения которого на данный момент у нас недостаточно подготовки. Все эти эффекты вместе, казалось бы, дожны требовать, чтобы пробная частица притягивалась к нижнему потоку.
Пробная частица не притягивается к нижнему потоку из-за зависящей от скорости силы, которая отталкивает частицу движущуюся в том же направлении, что и нижний поток. Этот зависящий от скорости гравитационный эффект является гравитомагнетизмом.[10]:245–253
Таким образом, материя, движущаяся через гравитамагнитное поле, подвержена так называемым эффектам увлечения инерциальных систем отсчёта, аналогичным электромагнитной индукции. Было предложено, что такие гравитамагнитные силы лежат в основе генерации релятивистских струй (джетов) (см. рис. 5-8), выбрасываемых некоторыми вращающимися сверхмассивными чёрными дырыми.[39][40]
Давление и напряжение[править | править код]
Величины, которые непосредственно связаны с энергией и импульсом, также должны быть источниками гравитации. Это внутреннее давление и механическое напряжение. Взятые вместе, масса-энергия, импульс, давление и напряжение служат источниками силы тяжести: в совокупности это всё то, что искривляет пространство-время.
Общая теория относительности предсказывает, что давление действует как источник гравитации с той же силой, что и плотность массы-энергии. Включение давления как источника силы тяжести приводит к резким различиям между предсказаниями общей теории относительности и прогнозами ньютоновской гравитации. Например, член давления устанавливает максимальный предел массы нейтронной звезды. Чем массивнее нейтронная звезда, тем больше давления требуется для удержания её веса в силе тяжести. Однако повышенное давление увеличивает силу тяжести, действующей на массу звезды. При определённой массе, определяемой пределом Толмена-Оппенгеймера-Волкова, процесс становится необратимым, и нейтронная звезда сжимается до чёрной дыры.[10]:243,280
Члены давления становятся весьма существенными при выполнении таких расчётов как гидродинамическое моделирование коллапса сверхновых.[41]
Экспериментальная проверка[править | править код]
Эти предсказания о роли давления, импульса и механического напряжения в качестве источников кривизны пространства-времени играют важную роль в общей теории относительности. Если рассмотреть давление, то в ранней Вселенной преобладало излучение,[42] и маловероятно, чтобы любые из соответствующих космологических данных (например, нуклеосинтез) могут быть воспроизведены, если бы давление не участвовало в гравитации, или если бы оно не имело такой же силы в качестве источника силы тяжести, как масса-энергия. Аналогично, математическая согласованность уравнений поля Эйнштейна была бы нарушена, если бы механическое напряжение не вносило вклад в силу тяжести.
Всё это хорошо, но есть ли какие-либо прямые, количественные экспериментальные или наблюдаемые измерения, которые подтверждают, что эти термины влияют на гравитацию?
Активная, пассивная и инерционная массы[править | править код]
Прежде чем обсуждать экспериментальные данные по различным источникам гравитации, нам нужно сначала обсудить различия Бонди между возможными типами массы: (1) активная масса () масса, которая действует как источник гравитационного поля; (2) пассивная масса () — масса, которая реагирует на гравитационное поле; (3) инерционная масса () — масса, которая реагирует на ускорение.[43]
- совпадает с тем, что мы ранее называли гравитационной массой () в нашем обсуждении принципа эквивалентности в разделе Основные положения.
В теории Ньютона,
- Третий закон действия и противодействия диктует, что и должны быть одинаковыми.
- С другой стороны, равны ли и это эмпирический результат.
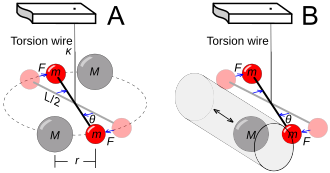
(A) Эксперимент Кавендиша
(B) Эксперимент Крейзера
В общей теории относительности,
- Равенство и продиктовано принципом эквивалентности.
- Нет принципа «действия и противодействия» с диктовкой любых отношений между и .[43]
Давление как источник гравитации[править | править код]
(слева) Этот светоотражатель оставлен на Луне астронавтами в миссии Аполлон-11.
(справа) Астрономы во всем мире ловили свет от светоотражателей, оставленных астронавтами Аполлона, и советских луноходов, чтобы измерить точное расстояние между Землёй и Луной.
Классический эксперимент по измерению силы источника гравитации (то есть его активной массы) был впервые проведён в 1797 году — Эксперимент Кавендиша (рис. 5-9а). Два маленьких но плотных шара подвешиваются на тонкой проволоке, образуя крутильные весы. Приближение двух больших масс близко к шарам приводит к заметному крутящему моменту. Учитывая размеры устройства и измеряемый коэффициент упругости подвеса, можно определить гравитационную постоянную G.
Изучение эффектов давления путём сжатия испытываемых масс является бесполезным, поскольку достижимые лабораторные давления незначительны по сравнению с массой-энергией металлического шарика.
Однако отталкивающее электромагнитное давление, возникающее при плотном сжатии протонов внутри атомных ядер, обычно составляет порядка 10 28 атм ≈ 1033 Па ≈ 1033 кг·с−2т1. Это составляет около 1 % от массовой плотности ядра примерно 1018кг/м3 (после факторизации в c 2 ≈ 9 × 1016 т2 c−2).[44]
Если давление не является источником гравитации, то отношение должно быть ниже для ядер с более высоким атомным номером Z, в котором больше электростатическое давление. Л. Б. Крейзер (1968) провёл эксперимент Кавендиша с использованием массы тефлона, суспендированной в смеси жидкостей трихлорэтилена и дибромэтана, имеющих ту же плавучую плотность, что и тефлон (рис. 5-9b). Фтор имеет атомный номер Z = 9, а бром имеет Z = 35. Крейцер обнаружил, что изменение массы тефлона не приводит к дифференциальному отклонению торсионного стержня, поэтому установление активной массы и пассивной массы эквивалентно точности 5 × 10−5.[45]
Хотя Крейцер первоначально считал этот эксперимент просто проверкой отношения активной массы к пассивной массе, Клиффорд Уилл (1976) переинтерпретировал эксперимент как фундаментальный тест на связывание источников с гравитационными полями.[46]
В 1986 году Бартлетт и Ван Бурен отметили, что лазерная локация Луны обнаружила смещение в 2 км между центром формы Луны и её центром масс. Это указывает на асимметрию распределения Fe (много в лунном ядре) и Al (много в её коре и мантии). Если бы давление не способствовало равномерности кривизны пространства-времени, как масса-энергия, луна не была бы на орбите, предсказанной классической механикой. Они использовали свои измерения для сужения пределов любых расхождений между активной и пассивной массой примерно до 1 × 10−12.[47]
Гравитомагнетизм[править | править код]
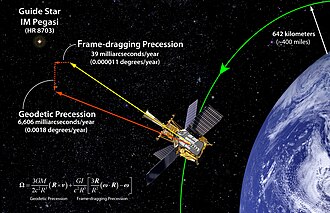
Существование гравитомагнетизма было доказано при помощи Gravity Probe B (GP-B), спутниковой миссии, которая была запущена 20 апреля 2004 года[48]. Фаза космического полёта продолжалась до 2005 года. Цель миссии состояла в том, чтобы измерить кривизну пространства-времени около Земли с особым упором на гравитомагнетизм.
Первоначальные результаты подтвердили относительно большую геодезическую прецессию (которая объясняется просто кривизной пространства-времени и также известна как прецессия де Ситтера) с точностью около 1 %. Значительно меньший эффект увлечения инерциальных систем отсчёта (который обусловлен гравитомагнетизмом и также известен как Эффект Лензе—Тирринга) было трудно измерить из-за неожиданных эффектов заряда, вызывающих переменный дрейф в гироскопах. Тем не менее, к , увлечения инерциальных систем отсчёта был подтверждён в пределах 15 % от ожидаемого результата[49], в то время как геодезическая прецессия была подтверждена до 0,5 %[50][51].
Последующие измерения увлечения инерциальных систем отсчёта с помощью лазерно-дальномерных наблюдений спутников LARES, LAGEOS-1 и LAGEOS-2 улучшили измерения GP-B, с результатами (по состоянию на 2016 год), демонстрирующим эффект в пределах 5 % от его теоретического значения[52], хотя были некоторые споры по поводу точности этого результата[53].
Ещё одна попытка — эксперимент «Гироскопы в общей теории относительности» (GINGER) — предполагает использование трёх 6-дюймовых кольцевых лазеров, установленных под прямым углом друг к другу на 1400 м над земной поверхностью для измерения этого эффекта[54][55].
Технические вопросы[править | править код]
Действительно ли пространство-время искривлено?[править | править код]
В конвенциональных взглядах Пуанкаре существенными критериями, согласно которым следует выбрать евклидову или неевклидову геометрию, является экономичность и простота. Реалист сказал бы, что Эйнштейн обнаружил, что пространство-время было неевклидовым. Традиционалист сказал бы, что Эйнштейн просто счёл более удобным использовать неевклидову геометрию. Традиционалист утверждал бы, что анализ Эйнштейна ничего не сказал о том, какая действительно геометрия пространства-времени.[56]
Другими словами,
- 1. Можно ли представить общую теорию относительности в терминах плоского пространства-времени?
- 2. Существуют ли ситуации, когда плоская пространственно-временная интерпретация общей теории относительности может быть более удобной, чем обычная искривлённая пространственно-временная интерпретация?
В ответ на первый вопрос ряд авторов, в том числе Дезер, Грищук, Розен, Вайнберг и т. д., представили различные формулировки гравитации как поля в плоском многообразии. Эти теории имеют разные названия, такие как «биметрическая гравитация», «теоретико-полевой подход к общей теории относительности» и т. д.[57][58][59][60] У Кип Торна есть популярный обзор этих теорий.[61]:397–403
Плоская пространственно-временная парадигма утверждает, что материя создаёт гравитационное поле, которое заставляет линейки сжиматься, когда они повёрнуты от периферической ориентации к радиальной, и это приводит к тому, что скорости тикания часов замедляются. Плоская пространственно-временная парадигма полностью эквивалентна искривлённой парадигме пространства-времени в том, что они обе представляют одни и те же физические явления. Однако их математические формулировки совершенно разные. Работая физики обычно переключаются между использованием методов искривлённого и плоского пространства-времени в зависимости от требований задачи. Плоская пространственно-временная парадигма оказывается особенно удобной при выполнении приближённых вычислений в слабых полях. Следовательно, при решении задач гравитационных волн будут использоваться методы плоского пространства-времени, а при анализе чёрных дыр будут использоваться методы искривлённого пространства-времени.
Геометрия Римана[править | править код]
Искривлённые многообразия[править | править код]
Привилегированное положение 3+1 пространства-времени[править | править код]
Существует два вида размерностей: пространственные и временные. Пространственную размерность обозначают буквой N, а временную буквой Т. Пространственно-временной континуум с размерностью N=3 и Т=1 имеет преимущество с точки зрения антропного принципа.
Пространство-время в культуре[править | править код]
Артур Шопенгауэр в 18-м параграфе труда «О четверояком корне закона достаточного основания» (1813) писал: «…только во времени представление сосуществования невозможно; в другой своей половине оно обусловлено представлением пространства, так как только во времени все есть одно после другого, в пространстве же — одно подле другого: таким образом, это представление возникает только из соединения времени и пространства».
Идея о едином пространстве-времени изложена Эдгаром Аланом По в его очерке о космологии, озаглавленном «Эврика» (1848): «Пространство и длительность суть одно».
В 1895 году в романе «Машина времени» Герберт Уэллс писал: «Между временем и тремя измерениями пространства нет никакой разницы, за исключением того, что во времени движется наше сознание», и что «…каждое реальное тело должно обладать четырьмя измерениями: оно должно иметь длину, ширину, высоту и продолжительность существования».
Заключение[править | править код]
Первый развёрнутый вариант модели естественного объединения пространства и времени, пространство Минковского, был создан Германом Минковским в 1908 году[62] на основе специальной теории относительности Эйнштейна, а несколько ранее (в 1905 году), ключевое продвижение на этом пути сделал Анри Пуанкаре, заложивший основы четырёхмерного пространственно-временного формализма.
Концепцию пространства-времени допускает и классическая механика[63], но в ней это объединение искусственно, так как пространство-время классической механики — прямое произведение пространства на время, то есть пространство и время независимы друг от друга. Однако уже классическая электродинамика требует при смене системы отсчёта преобразований координат, включающих время «наравне» с пространственными координатами (т. н. преобразований Лоренца), если желать, чтобы уравнения электродинамики имели одинаковый вид в любой инерциальной системе отсчёта. Непосредственно наблюдаемые временные характеристики электромагнитных процессов (периоды колебаний, времена распространения электромагнитных волн и т. п.) уже в классической электродинамике оказываются зависящими от системы отсчёта (или, иначе говоря, от относительного движения наблюдателя и объекта наблюдения), то есть оказываются не «абсолютными», а определённым образом связанными с пространственным движением и даже положением в пространстве системы отсчёта, что и явилось первым толчком для формирования современной физической концепции единого пространства-времени.
Ключевым математическим отличием пространства-времени (пространства Минковского, или, в случае общей теории относительности — четырёхмерного многообразия с лоренцевой метрикой) от обычного евклидова 4-мерного пространства является то, что при вычислении расстояния (интервала) квадраты значений разностей времени и длин пространственных координат берутся с противоположными знаками (в обычном пространстве соответствующие значения равноправны для любой оси координат и имеют одинаковый знак). Из этого вытекает следующее: прямая между двумя точками этого континуума (под прямой понимается движение по инерции) даёт максимальную продолжительность собственного времени (интервала). Для пространственной же длины прямая — минимальная, а не максимальная величина[64].
В контексте теории относительности время неотделимо от трёх пространственных измерений и зависит от скорости наблюдателя[note 7] (см. собственное время).
Концепция пространства-времени сыграла исторически ключевую роль в создании геометрической теории гравитации. В рамках общей теории относительности гравитационное поле сводится к проявлениям геометрии четырёхмерного пространства-времени, которое в этой теории не является плоским (гравитационный потенциал в ней отождествлён с метрикой пространства-времени).
Количество измерений, необходимых для описания Вселенной, окончательно не определено. Теория струн (суперструн), например, требовала наличия 10 (считая время), а теперь даже 11 измерений (в рамках М-теории). Предполагается, что дополнительные (ненаблюдаемые) 6 или 7 измерений свёрнуты (компактифицированы) до планковских размеров, так что экспериментально они пока не могут быть обнаружены. Ожидается, тем не менее, что эти измерения каким-то образом проявляют себя в макроскопическом масштабе. В самом старом — бозонном — варианте теория струн требует 26-мерного объемлющего пространства-времени; предполагается, что «лишние» измерения этой теории также должны или могут быть компактифицированы сначала до 10, сводясь таким образом к теории суперструн, а потом уже, как упомянуто здесь чуть выше, до 4 обычных измерений.
См. также[править | править код]
Примечания[править | править код]
- Комментарии
- ↑ В прямоугольной системе координат обычное вращение оставляет круг неизменным. В пространстве-времени гиперболическое вращение сохраняет гиперболическую метрику.
- ↑ Но не все эксперименты характеризуют эффект с точки зрения красного смещения. Например, был выбран эксперимент Айвса—Стилвелла для измерения поперечного синего смещения с использованием установки Мессбауэра в центре ротора центрифуги и приемника на ободе.
- ↑ Быстрота возникает естественным образом как координаты на чистом генераторе буста внутри алгебры Ли группы Лоренца. Аналогично, углы поворота естественным образом возникают в виде координат (по модулю 2) на чистом вращении Ли в алгебре Ли. (Вместе они координируют всю алгебру Ли). Заметным отличием является то, что результирующие вращения являются периодическими по углу поворота, а полученные ускорения не являются периодическими по быстроте (но скорее взаимно однозначными). Сходство между ускорениями и вращениями является формальным сходством.
- ↑ В теории относительности собственное ускорение — это физическое ускорение (то есть измеренное при помощи акселерометра ускорение), испытываемое объектом. Другими словами, это ускорение относительно свободного висящего или инерциального наблюдателя, который мгновенно находится в состоянии покоя относительно измеряемого объекта.
- ↑ Сам Ньютон остро осознавал присущие трудности с этими предположениями, но предположения были единственным способом, с которым он мог добиться прогресса. В 1692 году он написал своему другу Ричарду Бентли: «Это гравитация должна быть врождённой, неотъемлемой и существенной для Материи, так что одно тело может воздействовать на другого на расстоянии, через вакуум, без посредничества чего либо другого, через что их действие и сила могут передаваться от одного к другому, для меня настолько велика, что я не верю, что ни один Человек, имеющий компетенцию в философских вопросах, никогда не может попасть в него».
- ↑ Точнее, гравитационное поле соединяется с самим собой. В ньютоновской гравитации потенциал двух точечных масс - это просто сумма потенциалов двух масс, но это не относится к ОТО. Это можно рассматривать как результат принципа эквивалентности: если гравитация не соединялась сама с собой, две частицы, связанные их взаимным гравитационным притяжением, не имели бы такой же инерционной массы (из-за отрицательной энергии связи) в качестве своей гравитационной массы.[32]:112–113
- ↑ Притом, что формально переход к движущейся системе отсчёта аналогичен повороту осей в пространстве Минковского (и это даёт простой и компактный способ пересчёта реальных физических величин, то есть имеет вполне наблюдаемые нетривиальные физические следствия!), тем не менее, как бы не интерпретировать эту формальную аналогию с поворотом в обычном пространстве, на повороты в пространстве-времени наложены существенные физические ограничения, также определяющие ограничения аналогии пространства-времени с обычным евклидовым пространством, хотя бы и четырёхмерным (то есть описываемое в этом примечании — это ещё одна сторона качественного отличия пространства-время теории относительности от «просто» четырёхмерного пространства). Так, в рамках специальной теории относительности невозможен, а в рамках общей (где надёжный анализ всех сложных случаев сильно затруднён) — крайне сомнителен, плавный непрерывный поворот движения наблюдателя в сторону обратного движения по времени (тогда как в обычном пространстве можно поворачивать в любую сторону).
- ↑ Различные журналисты, просматривающие сценарии, представленные на этом рисунке, интерпретируют их по-разному в зависимости от их знания ситуации. (i) Первый репортёр, в центре массы частиц 2 и 3, но не подозревающий о большой массе 1, заключает, что сила отталкивания существует между частицами в сценарии А, в то время как сила притяжения существует между частицами в сценарии B. (ii) Второй репортёр, зная о большой массе 1, улыбается наивности первого репортёра. Этот второй репортёр знает, что на самом деле кажущиеся силы между частицами 2 and 3 действительно представляют собой приливные эффекты, возникающие в результате их дифференциального притяжения к массе 1. (iii) Третий репортёр, прошедший подготовку по общей теории относительности, знает, что на самом деле нет никаких сил, действующих между этими тремя объектами. Скорее всего, все три объекта движутся вдоль геодезических в пространстве-времени.
- Источники
- ↑ Точнее, почти равноправным: на самом деле практически в любой современной формулировке временное измерение сохраняет некоторое отличие от пространственных, хотя это часто замаскировано. Это отличие проявляется прежде всего в сигнатуре метрики пространства-времени (см. Пространство Минковского).
- ↑ Джордж Массер. Что есть пространство-время? // В мире науки. — 2018. — № 8—9. — С. 78—82.
- ↑ Rynasiewicz, Robert. «Newton’s Views on Space, Time, and Motion» Архивировано 11 декабря 2015 года.. Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 24 March 2017.
- ↑ 1 2 3 4 Collier, Peter. A Most Incomprehensible Thing: Notes Towards a Very Gentle Introduction to the Mathematics of Relativity (англ.). — 3rd. — Incomprehensible Books, 2017. — ISBN 9780957389465.
- ↑ Rowland, Todd Manifold. Wolfram Mathworld. Wolfram Research. Дата обращения: 24 марта 2017. Архивировано 13 марта 2017 года.
- ↑ French, A.P. Special Relativity. — Boca Raton, Florida: CRC Press, 1968. — С. 35—60. — ISBN 0748764224.
- ↑ 1 2 3 4 5 6 7 Taylor, Edwin F.; Wheeler, John Archibald. Spacetime Physics: Introduction to Special Relativity (англ.). — 1st. — San Francisco: Freeman, 1966. — ISBN 071670336X. Архивировано 6 мая 2012 года.
- ↑ Scherr, Rachel E.; Shaffer, Peter S.; Vokos, Stamatis. Student understanding of time in special relativity: Simultaneity and reference frames (англ.) // American Journal of Physics : journal. — 2001. — July (vol. 69, no. S1). — P. S24—S35. — doi:10.1119/1.1371254. — . — arXiv:physics/0207109. Архивировано 28 сентября 2018 года.
- ↑ Curtis, W. D.; Miller, F. R. Differential Manifolds and Theoretical Physics (англ.). — Academic Press, 1985. — P. 223. — ISBN 978-0-08-087435-7. Extract of page 223 Архивная копия от 13 июня 2020 на Wayback Machine
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Schutz, Bernard. Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity (англ.). — Reprint. — Cambridge: Cambridge University Press, 2004. — ISBN 0521455065. Архивировано 17 января 2023 года.
- ↑ Curiel, Erik; Bokulich, Peter Lightcones and Causal Structure. Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Дата обращения: 26 марта 2017. Архивировано 17 мая 2019 года.
- ↑ Savitt, Steven Being and Becoming in Modern Physics. 3. The Special Theory of Relativity. The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Дата обращения: 26 марта 2017. Архивировано 11 марта 2017 года.
- ↑ 1 2 3 4 5 6 Schutz, Bernard F. A first course in general relativity. — Cambridge, UK: Cambridge University Press, 1985. — С. 26. — ISBN 0521277035.
- ↑ 1 2 3 4 5 6 7 Weiss, Michael The Twin Paradox. The Physics and Relativity FAQ. Дата обращения: 10 апреля 2017. Архивировано 27 апреля 2017 года.
- ↑ Mould, Richard A. Basic Relativity. — 1st. — Springer, 1994. — С. 42. — ISBN 9780387952109.
- ↑ Lerner, Lawrence S. Physics for Scientists and Engineers, Volume 2 (англ.). — 1st. — Jones & Bartlett Pub, 1997. — P. 1047. — ISBN 9780763704605.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Bais, Sander. Very Special Relativity: An Illustrated Guide (англ.). — Cambridge, Massachusetts: Harvard University Press, 2007. — ISBN 067402611X.
- ↑ Forshaw, Jeffrey; Smith, Gavin. Dynamics and Relativity (англ.). — John Wiley & Sons, 2014. — P. 118. — ISBN 9781118933299.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Morin, David. Special Relativity for the Enthusiastic Beginner (англ.). — CreateSpace Independent Publishing Platform, 2017. — ISBN 9781542323512.
- ↑ Landau, L. D.; Lifshitz, E. M. The Classical Theory of Fields, Course of Theoretical Physics, Volume 2 (англ.). — 4th. — Amsterdam: Elsevier, 2006. — P. 1—24. — ISBN 9780750627689.
- ↑ Rose, H. H. Optics of high-performance electron microscopes (англ.) // Science and Technology of Advanced Materials : journal. — 2008. — 21 April (vol. 9, no. 1). — P. 014107. — doi:10.1088/0031-8949/9/1/014107. — . Архивировано 3 июля 2017 года.
- ↑ Griffiths, David J. Revolutions in Twentieth-Century Physics (англ.). — Cambridge: Cambridge University Press, 2013. — P. 60. — ISBN 9781107602175.
- ↑ Byers, Nina (1998). "E. Noether's Discovery of the Deep Connection Between Symmetries and Conservation Laws". arXiv:physics/9807044.
- ↑ Nave, R. Energetics of Charged Pion Decay. Hyperphysics. Department of Physics and Astronomy, Georgia State University. Дата обращения: 27 мая 2017. Архивировано 21 мая 2017 года.
- ↑ Thomas, George B.; Weir, Maurice D.; Hass, Joel; Giordano, Frank R. Thomas' Calculus: Early Transcendentals. — Eleventh. — Boston: Pearson Education, Inc., 2008. — С. 533. — ISBN 0321495756.
- ↑ Taylor, Edwin F.; Wheeler, John Archibald. Spacetime Physics. — 2nd. — W. H. Freeman, 1992. — ISBN 0716723271.
- ↑ 1 2 Gibbs, Philip Can Special Relativity Handle Acceleration? The Physics and Relativity FAQ. math.ucr.edu. Дата обращения: 28 мая 2017. Архивировано 7 июня 2017 года.
- ↑ Franklin, Jerrold. Lorentz contraction, Bell's spaceships, and rigid body motion in special relativity (англ.) // European Journal of Physics : journal. — 2010. — Vol. 31, no. 2. — P. 291—298. — doi:10.1088/0143-0807/31/2/006. — . — arXiv:0906.1919.
- ↑ Lorentz, H. A.; Einstein, A.; Minkowski, H.; Weyl, H. The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity (англ.). — Dover Publications, 1952. — ISBN 0486600815.
- ↑ 1 2 3 Mook, Delo E.; Vargish, Thoma s. Inside Relativity. — Princeton, New Jersey: Princeton University Press, 1987. — ISBN 0691084726.
- ↑ Mester, John Experimental Tests of General Relativity. Laboratoire Univers et Théories. Дата обращения: 9 июня 2017. Архивировано 9 июня 2017 года.
- ↑ 1 2 Carroll, Sean M. (2 December 1997). "Lecture Notes on General Relativity". arXiv:gr-qc/9712019.
- ↑ Le Verrier, Urbain. Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète (фр.) // Comptes rendus hebdomadaires des séances de l'Académie des Sciences : magazine. — 1859. — Vol. 49. — P. 379—383.
- ↑ Worrall, Simon The Hunt for Vulcan, the Planet That Wasn’t There. National Geographic. National Geographic. Дата обращения: 12 января 2024. Архивировано 4 июня 2023 года.
- ↑ Levine, Alaina G. May 29, 1919: Eddington Observes Solar Eclipse to Test General Relativity. APS News: This Month in Physics History. American Physical Society. Дата обращения: 12 июня 2017. Архивировано 2 июня 2017 года.
- ↑ Hobson, M. P.; Efstathiou, G.; Lasenby, A. N. General Relativity. — Cambridge: Cambridge University Press, 2006. — С. 176—179. — ISBN 9780521829519.
- ↑ Thorne, Kip S. Near zero: New Frontiers of Physics / Fairbank, J. D.; Deaver Jr., B. S.; Everitt, W. F.; Michelson, P. F.. — W. H. Freeman and Company, 1988. — С. 573—586. Архивировано 28 июля 2017 года.
- ↑ Feynman, R. P.; Leighton, R. B.; Sands, M. The Feynman Lectures on Physics, vol. 2. — New Millenium. — Basic Books, 1964. — С. 13—6 to 13—11. — ISBN 9780465024162.
- ↑ Williams, R. K. Extracting X rays, Ύ rays, and relativistic e−–e+ pairs from supermassive Kerr black holes using the Penrose mechanism (англ.) // Physical Review D : journal. — 1995. — Vol. 51, no. 10. — P. 5387—5427. — doi:10.1103/PhysRevD.51.5387. — . — PMID 10018300.
- ↑ Williams, R. K. Collimated escaping vortical polar e−–e+ jets intrinsically produced by rotating black holes and Penrose processes (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2004. — Vol. 611, no. 2. — P. 952—963. — doi:10.1086/422304. — . — arXiv:astro-ph/0404135.
- ↑ Kuroda, Takami; Kotake, Kei; Takiwaki, Tomoya. Fully General Relativistic Simulations of Core-Collapse Supernovae with An Approximate Neutrino Transport (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 2012. — Vol. 755. — P. 11. — doi:10.1088/0004-637X/755/1/11. — . — arXiv:1202.2487.
- ↑ Wollack, Edward J. Cosmology: The Study of the Universe. Universe 101: Big Bang Theory. NASA (10 декабря 2010). Дата обращения: 15 апреля 2017. Архивировано 14 мая 2011 года.
- ↑ 1 2 Bondi, Hermann. The Role of Gravitation in Physics: Report from the 1957 Chapel Hill Conference (англ.) / DeWitt, Cecile M.; Rickles, Dean. — Berlin: Max Planck Research Library, 1957. — P. 159—162. — ISBN 9783869319636. Архивировано 28 июля 2017 года.
- ↑ Crowell, Benjamin. General Relativity. — Fullerton, CA: Light and Matter, 2000. — С. 241—258. Архивировано 18 июня 2017 года.
- ↑ Kreuzer, L. B. Experimental measurement of the equivalence of active and passive gravitational mass (англ.) // Physical Review : journal. — 1968. — Vol. 169, no. 5. — P. 1007—1011. — doi:10.1103/PhysRev.169.1007. — .
- ↑ Will, C. M. Active mass in relativistic gravity-Theoretical interpretation of the Kreuzer experiment (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1976. — Vol. 204. — P. 224—234. — doi:10.1086/154164. — . Архивировано 28 сентября 2018 года.
- ↑ Bartlett, D. F.; Van Buren, Dave. Equivalence of active and passive gravitational mass using the moon (англ.) // Phys. Rev. Lett. : journal. — 1986. — Vol. 57, no. 1. — P. 21—24. — doi:10.1103/PhysRevLett.57.21. — . — PMID 10033347. Архивировано 28 сентября 2018 года.
- ↑ Gravity Probe B: FAQ. Дата обращения: 2 июля 2017. Архивировано 2 июня 2018 года.
- ↑ Gugliotta, G. (2009-02-16). "Perseverance Is Paying Off for a Test of Relativity in Space". New York Times. Архивировано из оригинала 3 сентября 2018. Дата обращения: 2 июля 2017.
- ↑ {{{2}}};{{{2}}}. Gravity Probe B Science Results—NASA Final Report (PDF) (2009). Дата обращения: 2 июля 2017. Архивировано 12 апреля 2017 года.
- ↑ Everitt et al. Gravity Probe B: Final Results of a Space Experiment to Test General Relativity (англ.) // Physical Review Letters : journal. — 2011. — Vol. 106, no. 22. — P. 221101. — doi:10.1103/PhysRevLett.106.221101. — . — arXiv:1105.3456. — PMID 21702590.
- ↑ Ciufolini, Ignazio; Paolozzi, Antonio Rolf Koenig; Pavlis, Erricos C.; Koenig, Rolf. A test of general relativity using the LARES and LAGEOS satellites and a GRACE Earth gravity model (англ.) // Eur Phys J C Part Fields : journal. — 2016. — Vol. 76, no. 3. — P. 120. — doi:10.1140/epjc/s10052-016-3961-8. — . — arXiv:1603.09674. — PMID 27471430. — PMC 4946852.
- ↑ Iorio, L. A comment on "A test of general relativity using the LARES and LAGEOS satellites and a GRACE Earth gravity model. Measurement of Earth's dragging of inertial frames," by I. Ciufolini et al (англ.) // The European Physical Journal C : journal. — 2017. — February (vol. 77, no. 2). — P. 73. — doi:10.1140/epjc/s10052-017-4607-1. — . — arXiv:1701.06474.
- ↑ Cartlidge, Edwin Underground ring lasers will put general relativity to the test. physicsworld.com. Institute of Physics. Дата обращения: 2 июля 2017. Архивировано 12 июля 2017 года.
- ↑ Einstein right using the most sensitive Earth rotation sensors ever made. Phys.org. Science X network. Дата обращения: 2 июля 2017. Архивировано 10 мая 2017 года.
- ↑ Murzi, Mauro Jules Henri Poincaré (1854–1912). Internet Encyclopedia of Philosophy (ISSN 2161-0002). Дата обращения: 9 апреля 2018. Архивировано 23 декабря 2020 года.
- ↑ Deser, S. Self-Interaction and Gauge Invariance (англ.) // General Relativity and Gravitation : journal. — 1970. — Vol. 1, no. 18. — P. 9—8. — doi:10.1007/BF00759198. — . — arXiv:gr-qc/0411023. Архивировано 9 апреля 2018 года.
- ↑ Grishchuk, L. P.; Petrov, A. N.; Popova, A. D. Exact Theory of the (Einstein) Gravitational Field in an Arbitrary Background Space-Time (англ.) // Communications in Mathematical Physics : journal. — 1984. — Vol. 94. — P. 379—396. — doi:10.1007/BF01224832. — . Архивировано 25 февраля 2021 года.
- ↑ Rosen, N. General Relativity and Flat Space I (англ.) // Physical Review : journal. — 1940. — Vol. 57, no. 2. — P. 147—150. — doi:10.1103/PhysRev.57.147. — .
- ↑ Weinberg, S. Derivation of Gauge Invariance and the Equivalence Principle from Lorentz Invariance of the S-Matrix (англ.) // Physics Letters : journal. — 1964. — Vol. 9, no. 4. — P. 357—359. — doi:10.1016/0031-9163(64)90396-8. — .
- ↑ Thorne, Kip. Black Holes & Time Warps: Einstein's Outrageous Legacy. — W. W. Norton & Company, 1995. — ISBN 978-0393312768.
- ↑ Hermann Minkowski, «Raum und Zeit», 80. Versammlung Deutscher Naturforscher (Köln, 1908). Published in Physikalische Zeitschrift 10 104—111 (1909) and Jahresbericht der Deutschen Mathematiker-Vereinigung 18 75-88 (1909).
- ↑ Работы В. И. Арнольда, в частности, «Математические методы классической механики».
- ↑ Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия: методы и приложения. Т. 1—3. Изд. 6-е. — М.: УРСС, 2013.
Ссылки[править | править код]
- Пространство и время — Физическая энциклопедия
- Penrose, Roger. The Road to Reality. — Oxford : Oxford University Press, 2004. — ISBN 0-679-45443-8.
- Spacetime Physics, Second Edition. — Internet Archive : W. H. Freeman, 1992. — ISBN 0-7167-2327-1.































































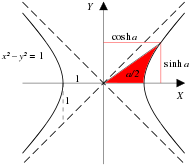











































































![{\displaystyle -\,\left(1+{\frac {2GM}{c^{2}r}}\right)\left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e004b8eb220d5cc0f0e835a4f9a584ebfdc3ef02)

![{\displaystyle \left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b88b386b994cad15b04251eedd908b3828db4d66)