Закон Снеллиуса
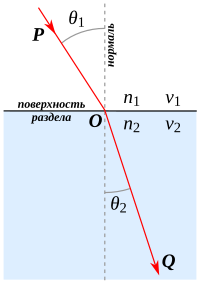

Зако́н Сне́ллиуса (также Снелля или Снелла) описывает преломление света на границе двух прозрачных сред. Также применим и для описания преломления волн другой природы, например, звуковых. Теоретическое объяснение закона Снеллиуса см. в статье Преломление.
Закон был открыт в 1621 году голландским математиком Виллебрордом Снеллиусом[1]. Несколько позднее опубликован (и, вероятно, независимо переоткрыт) Рене Декартом.
Формулировка[править | править код]
Угол падения света на поверхность связан с углом преломления соотношением:
- где — показатель преломления среды, из которой свет падает на границу раздела;
- — угол падения света — угол между падающим на поверхность лучом и нормалью к поверхности;
- — показатель преломления среды, в которую свет попадает, пройдя границу раздела;
- — угол преломления света — угол между прошедшим через поверхность лучом и нормалью к поверхности.
Пусть лежит в плоскости чертежа. Пусть ось направлена горизонтально, ось — вертикально. Из соображений симметрии следует, что и (для падающей, отраженной и преломленной волны, соответственно) должны лежать в одной плоскости.
Выделим из падающего луча плоскополяризованную составляющую, у которой угол между и плоскостью произволен. Тогда если выбрать начальную фазу равной нулю, то:
Результирующее поле в первой и второй среде равны соответственно:
Очевидно, что тангенциальные составляющие и должны быть равны на границе раздела то есть при
Тогда:
Для того, чтобы последнее уравнение выполнялось для всех необходимо, чтобы , а для того, чтобы оно выполнялось при всех необходимо, чтобы:
- где и — скорости волны в первой и второй среде соответственно.
Отсюда следует, что
Область применимости закона[править | править код]
Закон Снеллиуса хорошо определён для случая «геометрической оптики», то есть в случае, когда длина волны достаточно мала по сравнению с размерами преломляющей поверхности, вообще же говоря, работает в рамках приближённого описания, каковым и является геометрическая оптика.
Если имеет место полное внутреннее отражение (преломлённый луч отсутствует, падающий луч полностью отражается от границы раздела сред).
Следует заметить, что в случае анизотропных сред (например, кристаллов с низкой симметрией или механически деформированных твердых тел) преломление подчиняется несколько более сложному закону. При этом возможна зависимость направления преломленного луча не только от направления падающего, но и от его поляризации (см. двойное лучепреломление).
Закон Снеллиуса не описывает соотношение интенсивностей и поляризаций падающего, преломленного и отраженного лучей, рассматриваемые в более детальных формулах Френеля.
Исторический очерк[править | править код]
Первым закон преломления света, то есть зависимость угла преломления от угла падения, попытался экспериментально определить знаменитый античный астроном Клавдий Птолемей в пятой книге своего трактата «Оптика»[англ.]. Птолемей измерил, как меняется угол преломления в зависимости от угла падения при изменении последнего от до и составил таблицы для трёх вариантов смены среды: воздух-вода, воздух-стекло и вода-стекло. Например, для случая воздух-вода таблица Птолемея следующая (для сравнения приведены также современные данные и величина ошибки)[2][3]:
| Угол падения, градусов |
10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° |
| Данные Птолемея | 8° 0' | 15° 30' | 22° 30' | 29° 0' | 35° 0' | 40° 30' | 45° 30' | 50° 0' |
| Современные данные | 7° 29' | 14° 52' | 22° 01' | 28° 49' | 35° 04' | 40° 30' | 44° 48' | 47° 36' |
| Величина ошибки | +31' | +38' | +29' | +11' | −4' | 0' | +42' | +144' |
Историки пришли к выводу, что реально Птолемей измерял отклонение луча только в районе 60° и близких к нему углов, потому что во всех трёх таблицах для этого значения ошибка равна нулю, а для других углов выполнил линейную аппроксимацию с подобранными им коэффициентами. Однако на деле зависимость угла преломления от угла падения нелинейна, поэтому у Птолемея получились большие ошибки[2][4].
Арабский физик и астроном XI века Ибн аль-Хайсам в своей «Книге оптики[англ.] (1021 год) также рассуждает на эту тему и приводит свои таблицы, близкие к птолемеевским, однако не делает попыток выразить искомый закон математически[3].
В 1990 году арабский историк науки Рошди Рашед[англ.], специализирующийся на поиске арабского вклада в мировую науку, опубликовал статью, в которой сообщил, что он нашёл два фрагмента арабской рукописи малоизвестного учёного X века ибн Саля, одного из учителей Ибн аль-Хайсама. Рашед также сообщил, что он сумел реконструировать текст, из которого следует, что ибн Саль открыл и правильно сформулировал закон Снеллиуса. Независимые подтверждения для утверждений Рашеда пока отсутствуют. Требуется также объяснить, почему никто из последователей ибн Саля, включая его ученика Ибн аль-Хайсама, не упоминает об этом фундаментальном достижении, и почему сам ибн Саль не сообщает, какими экспериментами он доказал своё открытие[5][3].
В Европе первая формулировка закона преломления обнаружена в неопубликованной рукописи английского математика Томаса Хэрриота (1602 год). Немецкий астроном Иоганн Кеплер, занимавшийся проблемой выбора наилучшей формы зажигательных линз, просил Хэрриота сообщить подробности открытого тем закона, но Хэрриот ограничился отправкой уточнённых таблиц, сославшись на то, что плохое здоровье не позволяет ему выразить закон в форме, подходящей для публикации[6].
Ещё одно оставшееся неопубликованным открытие этого закона произошло в 1621 году, когда нидерландский математик Виллеброрд Снелл (Снеллиус) записал закон преломления в форме, равносильной современной: «в одних и тех же средах отношение косекансов углов падения и преломления остаётся постоянным». Скоропостижная смерть в 1626 году помешала Снеллу обнародовать своё открытие, однако слухи о нём разошлись, а набросок статьи Снелла сохранился и находится в библиотеке Амстердамского университета[7].
Позже «закон Снеллиуса» был независимо открыт и опубликован Рене Декартом в трактате «Рассуждение о методе» (приложение «Диоптрика», 1637). Приоритет Снелла установил Христиан Гюйгенс в 1703 году (в трактате «Диоптрика»), спустя 77 лет после смерти Снелла, когда этот закон уже был общеизвестен; Гюйгенс также обосновал (в труде «Трактат о свете[англ.]») вывод закона Снеллиуса из волновой теории света и принципа Гюйгенса — Френеля. Недоброжелатели обвинили Декарта в плагиате, подозревая, что во время одного из своих визитов в Лейден Декарт услышал об открытии Снелла и смог ознакомиться с его рукописями[8]. Однако никаких доказательств плагиата нет, а самостоятельный путь Декарта к этому открытию подробно изучен историками[9][10].
Принцип Ферма[править | править код]

Известный принцип[11] о движении светового луча по пути между двумя точками, который требует наименьшего времени можно использовать для доказательства закона преломления. Пусть скорость света в двух средах составляет и , тогда время движения между точками А и В зависит от выбора точки P на границе между средами:
Эта функция будет иметь минимум когда её производная равна нулю[12]:
Здесь синусы углов можно выразить через треугольники:
Производная приводится к виду
из чего следует, что
Это выражение представляет собой закон Снеллиуса[13].
Векторная формула[править | править код]
Пусть и лучевые векторы падающего и преломленного световых лучей, то есть векторы, указывающие направления лучей и имеющие длины и а единичный нормальный вектор к преломляющей поверхности в точке преломления. Тогда:
Примечания[править | править код]
- ↑ Снеллиус — латинизированная форма оригинальной фамилии Снелл
- ↑ 1 2 Бронштэн В. А. Клавдий Птолемей / Отв. ред. А. А. Гурштейн. — М.: Наука, 1988. — С. 157—161. — 239 с.
- ↑ 1 2 3 Sabra A. I. (1981), Theories of Light from Descartes to Newton, Издательство Кембриджского университета. (ср. Pavlos Mihas, Use of History in Developing ideas of refraction, lenses and rainbow, p. 5, Demokritus University, Фракия, Греция.)
- ↑ Ptolemy (ca. 100-ca. 170). Eric Weinstein's World of Scientific Biography. Дата обращения: 28 июля 2021. Архивировано 27 апреля 2006 года.
- ↑ Dr. Gorden Videen. Whose Law of Refraction? Архивная копия от 27 июля 2021 на Wayback Machine, Optics & Photonics News (May 2008) Архивная копия от 27 июля 2021 на Wayback Machine
- ↑ Kwan, A.; Dudley, J.; Lantz, E. (2002). "Who really discovered Snell's law?". PhysicsWorld. 15 (4): 64. doi:10.1088/2058-7058/15/4/44.
- ↑ Розенбергер Ф. История физики. — М.—Л.: ГИТТЛ, 1934. — Т. 2. — С. 94—95.
- ↑ Снеллиус // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II. — С. 32.
- ↑ Дорфман Я. Г. Всемирная история физики. С древнейших времён до конца XVIII века. — Изд. 3-е. — М.: ЛКИ, 2010. — С. 198—199. — 352 с. — ISBN 978-5-382-01091-5.
- ↑ Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Том 3: Излучение. Волны. Кванты. Перевод с английского (издание 4). — Эдиториал УРСС. — ISBN 5-354-00701-1.
- ↑ Ландсберг, Г. С. Оптика: учебное пособие для вузов. — 6-е изд. стереот. — М.: ФИЗМАТЛИТ, 2003. — С. 252. — 848 с. — ISBN 5-9221-0314-8.
- ↑ Снелля закон // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.









































