Осциллятор Ван дер Поля
| Осциллятор Ван дер Поля | |
|---|---|
 | |
| Названо в честь | Балтазар Ван дер Пол |
| Определяющая формула | |
Осциллятор Ван дер Поля — осциллятор с нелинейным затуханием. Математически моделируется уравнением
- , где
- — координата точки, зависящая от времени ;
- — коэффициент, характеризующий нелинейность и силу затухания колебаний.
История[править | править код]
Осциллятор Ван дер Поля был предложен голландским инженером и физиком Бальтазаром ван дер Полем, во время его работы в компании Philips.[1] Ван дер Полем были найдены устойчивые колебания, которые были названы релаксационными,[2] известные как «предельные циклы». В сентябре 1927 года Ван дер Поль и его коллега ван дер Марк сообщили,[3] что на определённых частотах были зафиксированы шумы, всегда находящиеся рядом с собственными частотами волн. Это было одним из первых наблюдений детерминированного хаоса.[4]
Уравнение Ван дер Поля применяется и в физике, и в биологии. Так, например, в биологии создана модель ФитцХью — Нагумо. Данное уравнение также было использовано в сейсмологии для моделирования геологических разломов.[5]
Двумерный случай[править | править код]
С помощью теоремы Льенара можно доказать, что система имеет предельный цикл. Из данной теоремы следует, что . Отсюда можно вывести[6] уравнения осциллятора Ван дер Поля для двумерного случая:
- .
Можно также совершить другую замену и получить
- .
Осциллятор со свободными колебаниями[править | править код]
У осциллятора Ван дер Поля существуют два интересных режима: при и при . Очевидно, что третьего режима — — не существует, так как затухание в системе не может быть отрицательным.
- 1) Когда , то есть осциллятор рассчитывается без затухания, то указанные выше уравнения преобразуются к виду
- .
- Это уравнение гармонического осциллятора.
- 2) При система имеет некие предельные циклы. Чем дальше от нуля, тем колебания осциллятора менее похожи на гармонические.
Вынужденные колебания[править | править код]
Вынужденные колебания осциллятора Ван дер Поля как с потерями энергии, так и без оных рассчитываются по формуле
- , где
- — амплитуда внешнего гармонического сигнала,
- — его угловая частота.
Галерея[править | править код]
-
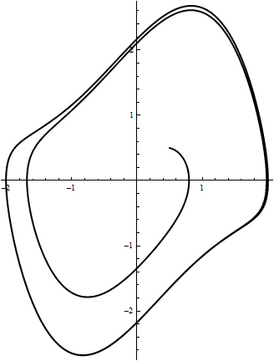
Фазовый портрет осциллятора. Виден предельный цикл.
-
Изменение формы предельного цикла при изменении
-
Релаксационные колебания осциллятора. .
-
Хаотичное поведение осциллятора при воздействии внешней гармонической вынуждающей силы.
-
Принципиальная схема на триоде.
Примечания[править | править код]
- ↑ Cartwright, M.L., «Balthazar van der Pol» Архивная копия от 18 октября 2019 на Wayback Machine, J. London Math. Soc., 35, 367—376, (1960).
- ↑ Van der Pol, B., «On relaxation-oscillations», The London, Edinburgh and Dublin Phil. Mag. & J. of Sci., 2(7), 978—992 (1927).
- ↑ Van der Pol, B. and Van der Mark, J., «Frequency demultiplication», Nature, 120, 363—364, (1927).
- ↑ Kanamaru, T., «Van der Pol oscillator» Архивная копия от 9 июля 2009 на Wayback Machine, Scholarpedia, 2(1), 2202, (2007).
- ↑ Cartwright, J., Eguiluz, V., Hernandez-Garcia, E. and Piro, O., «Dynamics of elastic excitable media», Internat. J. Bifur. Chaos Appl. Sci. Engrg., 9, 2197—2202, (1999).
- ↑ Kaplan, D. and Glass, L., Understanding Nonlinear Dynamics, Springer, 240—244, (1995)



















