Теорема Вивиани
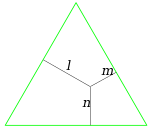
Теорема Вивиани — утверждение в геометрии треугольника, согласно которому сумма расстояний от произвольной точки внутри равностороннего треугольника до его сторон постоянна и равна высоте треугольника. Названа по имени итальянского математика Винченцо Вивиани.
В части постоянства суммы расстояний от произвольной внутренней точки до сторон утверждение может быть обобщено на равносторонние многоугольники и многоугольники с равными углами[1].
Доказательство[править | править код]
Теорема может быть доказана путём сравнения площадей треугольников. Пусть — равносторонний треугольник, в котором — высота, — длина каждой из сторон. Точка выбирается произвольно внутри треугольника, и тогда , , — расстояния от точки до сторон треугольника. Тогда площадь можно определить следующим образом:
- ,
из чего вытекают следующие соотношения:
- ,
то есть:
- .
Приложения[править | править код]

ВПВ — верхний предел взрываемости;
НПВ — нижний предел взрываемости;
ПК — пороговая концентрация взрываемости.
Теорема Вивиани позволяет получать координаты точек на трёхкомпонентные диаграммы путём проведения линий, параллельных сторонам равностороннего треугольника. В частности, таким образом можно строить диаграммы воспламеняемости.
В более общем случае, они позволяют таким же образом задавать координаты на правильном симплексе.
Примечания[править | править код]
- ↑ Elias Abboud «On Viviani’s Theorem and its Extensions» Архивная копия от 25 февраля 2018 на Wayback Machine pp. 2, 11
Ссылки[править | править код]
- Weisstein, Eric W. Viviani's Theorem (англ.) на сайте Wolfram MathWorld.
- Li Zhou, Viviani Polytopes and Fermat Points
- Viviani’s Theorem: What is it? at Cut the knot.
- Viviani’s Theorem by Jay Warendorff, the Wolfram Demonstrations Project.
- Viviani's theorem: Visualization + Proof на YouTube










