Дуговая диаграмма

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску
Дуговая диаграмма графа Голднера–Харари. Красный пунктирный отрезок показывает, где можно разбить граф, чтобы сделать его гамильтоновым.

Дуговая диаграмма — это стиль представления графа, в котором вершины располагаются вдоль прямой на евклидовой плоскости, а рёбра рисуются в виде полуокружностей на одной из двух полуплоскостей, либо в виде гладких кривых, образованных полуокружностями. В некоторых случаях отрезки прямой также используются для представления рёбер графа, если они соединяют соседние вершины на прямой.

Название «дуговая диаграмма» для такого представления графов является преемником использования аналогичного типа диаграмм Ваттенберга[1], которые он использовал для визуализации повторяющихся фрагментов строк, соединяя пары одинаковых подстрок. Тем не менее, сам стиль представления графа много старше названия и датируется работами Саати[2] и Никольсона[3], которые использовали дуговые диаграммы для изучения числа пересечений графов. Более старое, но менее используемое название дуговых диаграмм —линейное вложение[4].

Хир, Босток и Огиветски[5] написал, что дуговые диаграммы «не могут выражать полной структуры графа так же эффективно, как это делает двумерное представление», но позволяет проще представить многомерные данные, связанные с вершинами графами.

Планарные графы

[править | править код]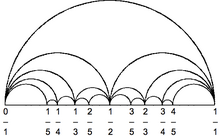
Диаграмма Фарея

Как заметил Никольсон[3], любое вложение графа в плоскость может быть преобразовано в дуговую диаграмму без изменения числа пересечений. В частности, любой планарный граф имеет планарную дуговую диаграмму. Однако такое вложение может потребовать использования более одной полуокружности для рисования некоторых рёбер графа.

Если граф нарисован без пересечений дуг в виде дуговой диаграммы, в которой каждое ребро представлено одной полуокружностью, рисунок является двустраничным книжным вложением, что возможно только для подгамильтоновых графов, подмножества планарных графов[6]. Например, максимальный планарный граф[англ.] имеет такое вложение тогда и только тогда, когда он содержит гамильтонов цикл. Таким образом, негамильтонов максимальный планарный граф, такой как граф Голднера–Харари, не может иметь планарного вложения с одной полуокружностью на ребро. Проверка, имеет ли данный граф дуговую диаграмму без пересечений этого типа (или, эквивалентно, книжная толщина графа равна двум), является NP-полной задачей[7].

Однако любой планарный граф имеет дуговую диаграмму, в которой каждое ребро представлено в виде бидуги, состоящей не более чем из двух полуокружностей. Более строго, любой st-планарный ориентированный граф (планарный направленный ациклический граф с одним источником и одним стоком, оба на внешней грани) имеет дуговую диаграмму, в которой любое ребро образует монотонную кривую, все кривые (рёбра) направлены в одну сторону[8]. Для неориентированных планарных графов одним из способов построения дуговой диаграммы максимум с двумя полуокружностями на ребро является разделение графа и добавление дополнительных рёбер с целью получить гамильтонов цикл (при этом рёбра делятся максимум на две части), затем используется порядок вдоль гамильтонова цикла в качестве порядка следования вершин на прямой[9].

Минимизация пересечений

[править | править код]

Поскольку проверка, имеет ли данный граф дуговую диаграмму без пересечений с одной полуокружностью на ребро, является NP-полной задачей, является также NP-трудной задачей поиск дуговой диаграммы, минимизирующей число пересечений. Задача минимизации числа пересечений остаётся NP-трудной для непланарных графов, даже если порядок вершин вдоль прямой уже задан[4]. Однако, в случае заданного порядка вершин, вложение без пересечений (если таковое существует) может быть найдено за полиномиальное время путём перевода задачи в задачу 2-выполнимости[англ.], в которой переменные представляют расположение каждой дуги, а ограничения предотвращают расположение двух пересекающихся рёбер по одну сторону от прямой с вершинами[10]. Кроме того, в случае фиксированного расположения вершин вложение с минимизацией числа пересечений может быть аппроксимировано путём решения задачи максимального разреза во вспмогательном графе, который представляет полуокружности и их потенциальные пересечения[11].

Кимиковский, Шоуп[12][13], Хе, Сикора и Врто[14] обсуждали эвристические алгоритмы поиска дуговых диаграмм с несколькими пересечениями.

Ориентация по часовой стрелке

[править | править код]

Для представления ориентированных графов общим соглашением является направление дуг по часовой стрелке, так что дуги, направленные слева направо, рисуются над прямой, а дуги справа налево рисуются под прямой. Это соглашение об ориентации по часовой стрелке разрабатывалось как часть другого стиля представления графа группой, в которую входили Фекете, Ванг, Данг и Арис[15], а к дуговым диаграммам этот стиль применили Преториус и ван Вейк[16].

Другое использование

[править | править код]

Дуговые диаграммы использовал Брандес[17] для визуализации диаграмм состояний сдвигового региста[англ.], а также Джиджев и Врто[18] для доказательства, что число пересечений любого графа по меньшей мере равно квадрату его ширины разреза.

Примечания

[править | править код]
  1. ↑ Wattenberg, 2002.
  2. ↑ Saaty, 1964.
  3. ↑ 1 2 Nicholson, 1968.
  4. ↑ 1 2 Masuda, Nakajima, Kashiwabara, Fujisawa, 1990.
  5. ↑ Heer, Bostock, Ogievetsky, 2010.
  6. ↑ Приложение полуокружностей для рисования рёбер в книжном вложении было уже использовано Бернхартом и Кайненом в 1979 (Bernhart, Kainen 1979), но явная связь дуговых диаграмм с двустраничными вложениями, видимо, принадлежит Масуде, Накаджиме, Кашивабаре и Фуджисаве (Masuda, Nakajima, Kashiwabara, Fujisawa 1990).
  7. ↑ Chung, Leighton, Rosenberg, 1987.
  8. ↑ Giordano, Liotta, Mchedlidze, Symvonis, 2007.
  9. ↑ Bekos, Kaufmann, Kobourov, Symvonis, 2013.
  10. ↑ Efrat, Erten, Kobourov, 2007.
  11. ↑ Cimikowski, Mumey, 2007.
  12. ↑ Cimikowski, Shope, 1996.
  13. ↑ Cimikowski, 2002.
  14. ↑ He, Sýkora, Vrt'o, 2005.
  15. ↑ Fekete, Wang, Dang, Aris, 2003.
  16. ↑ Pretorius, van Wijk, 2007.
  17. ↑ Brandes, 1999.
  18. ↑ Djidjev, Vrt'o, 2002.

Литература

[править | править код]
  • Michael A. Bekos, Michael Kaufmann, Stephen G. Kobourov, Antonios Symvonis. Graph Drawing: 20th International Symposium, GD 2012, Redmond, WA, USA, September 19–21, 2012, Revised Selected Papers. — Springer, 2013. — Т. 7704. — С. 150–161. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-642-36763-2_14.
  • Frank R. Bernhart, Paul C. Kainen. The book thickness of a graph // Journal of Combinatorial Theory. — 1979. — Т. 27, вып. 3. — С. 320–331. — doi:10.1016/0095-8956(79)90021-2.
  • Ulrik Brandes. Graph Drawing: 7th International Symposium, GD’99, Štiřín Castle, Czech Republic September 15–19, 1999, Proceedings. — Springer, 1999. — Т. 1731. — С. 410–415. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-46648-7_42.
  • Fan R. K. Chung, Frank T. Leighton, Arnold L. Rosenberg. Embedding graphs in books: A layout problem with applications to VLSI design // SIAM Journal on Algebraic and Discrete Methods. — 1987. — Т. 8. — С. 33–58. — doi:10.1137/0608002..
  • Robert Cimikowski. Algorithms for the fixed linear crossing number problem // Discrete Applied Mathematics. — 2002. — Т. 122. — С. 93–115. — doi:10.1016/S0166-218X(01)00314-6.
  • Robert Cimikowski, Brendan Mumey. Approximating the fixed linear crossing number // Discrete Applied Mathematics. — 2007. — Т. 155. — С. 2202–2210. — doi:10.1016/j.dam.2007.05.009.
  • Robert Cimikowski, Paul Shope. A neural-network algorithm for a graph layout problem // IEEE Transactions on Neural Networks. — 1996. — Т. 7. — С. 341–345. — doi:10.1109/72.485670.
  • Hristo Djidjev, Imrich Vrt'o. Graph Drawing: 9th International Symposium, GD 2001, Vienna, Austria, September 23–26, 2001, Revised Papers. — Springer, 2002. — Т. 2265. — С. 96–101. — (Lecture Notes in Computer Science). — doi:10.1007/3-540-45848-4_8..
  • Alon Efrat, Cesim Erten, Stephen G. Kobourov. Fixed-location circular arc drawing of planar graphs // Journal of Graph Algorithms and Applications. — 2007. — Т. 11. — С. 145–164. — doi:10.7155/jgaa.00140.
  • Jean-Daniel Fekete, David Wang, Niem Dang, Aleks Aris, Catherine Plaisant. IEEE Symp. on Information Visualization, Poster Compendium. — 2003. — С. 82–83.
  • Francesco Giordano, Giuseppe Liotta, Tamara Mchedlidze, Antonios Symvonis. Algorithms and Computation: 18th International Symposium, ISAAC 2007, Sendai, Japan, December 17-19, 2007, Proceedings. — Springer, 2007. — Т. 4835. — С. 172–183. — (Lecture Notes in Computer Science). — doi:10.1007/978-3-540-77120-3_17.
  • Hongmei He, Ondrej Sýkora, Imrich Vrt'o. Crossing Minimisation Heuristics for 2-page Drawings // Electronic Notes in Discrete Mathematics. — 2005. — Т. 22. — С. 527–534. — doi:10.1016/j.endm.2005.06.088.
  • Jeffrey Heer, Michael Bostock, Vadim Ogievetsky. A tour through the visualization zoo // Communications of the ACM. — 2010. — Т. 53. — С. 59–67. — doi:10.1145/1743546.1743567.
  • Sumio Masuda, Kazuo Nakajima, Toshinobu Kashiwabara, Toshio Fujisawa. Crossing minimization in linear embeddings of graphs // IEEE Transactions on Computers. — 1990. — Т. 39. — С. 124–127. — doi:10.1109/12.46286.
  • T. A. J. Nicholson. Permutation procedure for minimising the number of crossings in a network // Proceedings of the Institution of Electrical Engineers. — 1968. — Т. 115. — С. 21–26. — doi:10.1049/piee.1968.0004.
  • A. J. Pretorius, J. J. van Wijk. Bridging the semantic gap: Visualizing transition graphs with user-defined diagrams // IEEE Computer Graphics and Applications. — 2007. — Т. 27. — С. 58–66. — doi:10.1109/MCG.2007.121.
  • Thomas L. Saaty. The minimum number of intersections in complete graphs // Proceedings of the National Academy of Sciences of the United States of America. — 1964. — Т. 52. — С. 688–690. — doi:10.1073/pnas.52.3.688.
  • M. Wattenberg. Proc. IEEE Symposium o nInformation Visualization (INFOVIS 2002). — 2002. — С. 110–116. — doi:10.1109/INFVIS.2002.1173155.
Источник — https://ru.wikipedia.org/w/index.php?title=Дуговая_диаграмма&oldid=114535623