Угловое разрешение (теория графов)

Рисунок этого графа гиперкуба имеет угловое разрешение $\pi /4$.

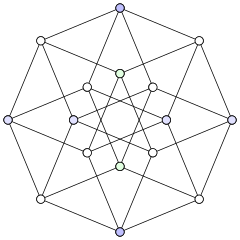
Угловое разрешение рисунка графа относится к самому острому углу, образованному любыми двумя рёбрами, которые встречаются в одной вершине рисунка.

Свойства

Связь со степенью вершины

Форман с соавторами заметили, что любой рисунок графа с рёбрами-отрезками с максимальной степенью d имеет угловое разрешение, не превосходящее $2\pi /d$ — если v является вершиной со степенью d, то рёбра, инцидентные v, разбивают пространство вокруг вершины v на d клиньев с суммарным углом $2\pi$, а наименьший из этих клиньев должен иметь угол, не превосходящий $2\pi /d$. Более строго, если граф является d-регулярным, он должен иметь угловое разрешение, меньшее ${\frac {\pi }{d-1}}$, поскольку это лучшее разрешение, которое может быть получено для вершины на выпуклой оболочке рисунка.

Связь с раскраской графа

Как показали Форман с соавторами, наибольшее возможное угловое разрешение графа G тесно связано с хроматическим числом квадрата графа G², то есть графа с тем же набором вершин, в котором каждая пара вершин соединена ребром, если расстояние между ними в графе G не превосходит двух. Если граф G² может быть раскрашен в $\chi$ цветов, то G может быть нарисован с угловым разрешением $\pi /\chi -\epsilon$ для любого $\epsilon >0$, если назначить различные цвета вершинам правильного $\chi$-угольника и разместить каждую вершину графа G рядом с вершиной многоугольника с тем же цветом. Используя это построение, они показали, что любой граф с максимальной степенью d имеет рисунок с угловым разрешением, пропорциональным 1/d². Эта граница близка к точной — они использовали вероятностный метод для доказательства существования графов с максимальной степенью d, все рисунки которых имеют угловое разрешение $O\left({\frac {\log d}{d^{2}}}\right)$.

Существование оптимальных рисунков

Форман с соавторами привели пример, показывающий, что существуют графы, не имеющие рисунки с максимальным возможным угловым разрешением. Напротив, эти графы имеют семейство рисунков, угловые разрешения которых стремятся к некоторому ограниченному значения, но не достигают его. Конкретно, они представили граф с 11 вершинами, который имеет рисунок с угловым разрешением $\pi /3-\epsilon$ для любого $\epsilon >0$, но не имеет рисунка с угловым разрешением, в точности равным $\pi /3$.

Специальные классы графов

Деревья

Любое дерево может быть нарисовано таким образом, что рёбра равномерно распределены вокруг каждой вершины, свойство, известное как совершенное угловое разрешение . Более того, если рёбра могут свободно переставляться вокруг каждой вершины, то такой рисунок возможен без пересечений с рёбрами длиной единица или более, а также весь рисунок помещается в прямоугольник полиномиальной площади. Однако, если циклическое упорядочение рёбер вокруг каждой вершины уже задано как часть условия задачи, то получение углового разрешения без пересечений может иногда потребовать экспоненциальной площади.

Внешнепланарные графы

Совершенное угловое разрешение не всегда возможно для внешнепланарных графов, поскольку вершины на выпуклой оболочки рисунка со степенью, большей единицы, не могут иметь инцидентные ей рёбра, равномерно распределённые вокруг вершины. Тем не менее, любой внешнепланарный граф с максимальной степенью d имеет внешнепланарный рисунок с угловым разрешением, пропорциональным 1/d.

Планарные графы

Для планарных графов с максимальной степенью d техника раскрашивания квадрата графа Формана (с соавторами) даёт рисунок с угловым разрешением, пропорциональным 1/d, поскольку квадрат планарного графа должен иметь хроматическое число, пропорциональное d. Вегнер высказал в 1977 году гипотезу, что хроматическое число квадрата планарного графа не превосходит $\max \left(d+5,{\frac {3d}{2}}+1\right)$ и известно, что хроматическое число не превосходит ${\frac {5d}{3}}+O(1)$. Однако рисунок, получающийся по этой технике, в общем случае не планарен.

Для некоторых планарных графов оптимальное угловое разрешение планарного рисунка с рёбрами в виде отрезков равно O(1/d³), где d является степенью графа. Кроме того, такие рисунки могут вынужденно иметь очень длинные рёбра, более длинные, чем экспоненциальный множитель от самого короткого ребра рисунка. Малиц и Папакостас использовали теорему об упаковке кругов, чтобы показать, что любой планарный граф с максимальной степенью d имеет планарный рисунок, угловое разрешение которого в худшем случае является экспоненциальной функцией от d и не зависящей от числа вершин графа.

Вычислительная сложность

Задача определения, имеет ли данный граф с максимальной степенью d рисунок с угловым разрешением $2\pi /d$, NP-трудна даже в специальном случае d=4. Однако для некоторых ограниченных классов рисунков, включая рисунки деревьев, в которых распространение листьев до бесконечности даёт выпуклое разбиение плоскости, как и рисунки планарных графов, в которых каждая ограниченная грань является центрально симметричным многоугольником, рисунок с оптимальным угловым разрешением может быть найден за полиномиальное время.

История

Угловое разрешение определили Форман с соавторами.

Хотя оно первоначально было определено для рисунков графов с прямолинейными рёбрами, позднее авторы исследовали угловое разрешение рисунков, в которых рёбра являются ломаными, дугами окружностей или сплайнами.

Угловое разрешение графа тесно связано с его разрешением пересечений, углам, образованным пересечениями в рисунке графа. В частности, рисование графов под прямыми углами ищет представление, которое обеспечивает, чтобы все эти углы были прямыми, что является наибольшим возможным углом пересечения