Восходящее планарное представление

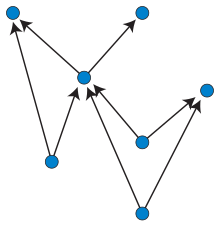
Восходящее планарное представление

Этот планарный ориентированный ациклический граф не имеет восходящего планарного представления, поскольку его источник и сток не могут быть представлены на одной грани

Восходящее планарное представление направленного ациклического графа — это вложение графа в евклидово пространство, в котором рёбра представлены как непересекающиеся монотонно возрастающие кривые. То есть, кривая, представляющая любое ребро, должна иметь свойство, что любая горизонтальная прямая пересекает его максимум в одной точке, и никакие два ребра не могут пересекаться, разве что на концах. В этом смысле это идеальный случай для послойного рисования графа, стиля представления графа, в котором монотонные кривые могут пересекаться, но в которых число пересечений минимально.

Описания

Направленный ациклический граф должен быть планарным, чтобы иметь восходящее планарное представление, но не всякий планарный ациклический граф имеет такое представление. Среди всех планарных направленных ациклических графов с единственным источником (вершиной, не имеющей входящих дуг) и стоком (вершиной, не имеющей исходящих дуг), графы с восходящими планарными представлениями — это st-планарные графы, планарные графы, в которых источник и сток принадлежат одной и той же грани по меньшей мере для одного планарного вложения графа. Более обще, граф G имеет восходящее планарное представление тогда и только тогда, когда он ориентированный, ациклический и является подграфом st-планарного графа на том же самом наборе вершин.

В восходящем вложении множество входящих и исходящих дуг, инцидентных каждой вершине, следуют подряд в циклическом порядке дуг в вершине. Говорят, что планарное вложение заданного направленного ациклического графа бимодально, если оно обладает таким свойством. Кроме того, угол между двумя последовательными дугами с той же ориентацией в заданной вершине может быть помечен как малый, если он меньше $\pi$, или большой, если он больше $\pi$. Каждый сток должен иметь в точности один большой угол и любая вершина, не являющаяся ни источником, ни стоком, не должна иметь большого угла. Кроме того, каждая внутренняя грань представления должна иметь на два больше малых углов, чем больших, а внешняя грань должна иметь на два больше больших угла, чем малых углов. Правильное назначение — это разметка углов, которая удовлетворяет описанным свойствам. Любое восходящее вложение имеет правильное назначение. В обратную сторону, любой направленный ациклический граф, имеющий бимодальное планарное вложение с правильным назначением имеет восходящее планарное представление, которое может быть построено за линейное время.

Другое описание возможно для графов с единственным источником. В этом случае восходящее планарное вложение должно иметь источник на внешней грани и любой неориентированный цикл в графе должен иметь по меньшей мере одну вершину, в которой обе дуги цикла входящие (например, вершина, находящаяся на самом верху рисунка). Обратно, если вложение имеет оба этих свойства, то это эквивалентно восходящему вложению.

Вычислительная сложность

Известно, что некоторые специальные случаи проверки восходящей планарности можно осуществить за полиномиальное время:

• Проверку, является ли граф st-планарным, можно осуществить за линейное время путём добавления ребра из s в t и проверки, является ли оставшийся граф планарным. Вдоль тех же линий можно построить восходящее планарное представление (если существует) направленного ациклического графа с единственным источником и стоком за линейное время.
• Проверку, можно ли ориентированный граф с фиксированным планарным вложением нарисовать как восходящий планарный с совместимым вложением, можно выполнить путём проверки, что вложение является бимодальным, и моделирования задачи совместимого назначения как задачи о потоке в сети. Время работы линейно от размера входного графа и полиномиально от числа источников и стоков.
• Поскольку направленные полиэдральные графы имеют единственное планарное вложение, существование восходящего планарного представления для этих графов может быть проверено за полиномиальное время.
• Проверка, имеет ли внешнепланарный ориентированный ациклический граф восходящее планарное представление, также полиномиальна.
• Любой параллельно-последовательный граф, ориентированный согласно параллельно-последовательной структуре, является восходяще планарным. Восходящее планарное представление может быть построено прямо из параллельно-последовательного разложения графа. Более обще, произвольная ориентация неориентированных параллельно-последовательных графов может быть проверена на восходящую планарность за полиномиальное время.
• Любое ориентированное дерево восходяще планарно.
• Любой двудольный планарный граф с рёбрами, ориентированными из одной доли в другую, восходяще планарен.
• Известен более сложный алгоритм полиномиального времени для проверки восходящей планарности графов, имеющих единственный источник, но несколько стоков, или наоборот.
• Проверка восходящей планарности может быть осуществлена за полиномиальное время, если имеется постоянное число трисвязных компонент из числа вершинных сечений и эта проверка фиксированно-параметрически разрешима по этим двум числам. Проверка также фиксированно-параметрически разрешима по цикломатическому числу входного графа.
• Если y-координаты всех вершин фиксированы, то x-координаты, которые делают представление восходяще планарным, можно найти за полиномиальное время.

Однако задача определения, имеет ли восходящее планарное представление планарный направленный ациклический граф с несколькими источниками и несколькими стоками, является NP-полной.

Рисование прямыми отрезками и требования площади

Теорема Фари утверждает, что любой планарный граф имеет представление, в котором рёбра представлены прямолинейными отрезками, и то же самое верно для восходящего планарного представления — любой восходящий планарный граф имеет восходящее планарное представление с дугами в виде прямолинейных отрезков. Прямолинейное восходящее представление транзитивно сокращённого st-планарного графа может быть получено с помощью техники доминирующего рисования со всеми вершинами, имеющими целых координат в решётке $n\times n$. Однако, некоторые другие восходящие планарные графы могут потребовать экспоненциальную площадь для всех их прямолинейных восходящих планарных представлений. Если способ вложения фиксирован, даже направленные параллельно-серийные графы и ориентированные деревья могут потребовать экспоненциальной площади.

Диаграммы Хассе

Восходящие планарные представления особо важны для диаграмм Хассе частично упорядоченных множеств, так как эти диаграммы обычно требуется рисовать в восходящем стиле. В терминах теории графов это соответствует транзитивно сокращенным направленным ациклическим графам. Такой граф можно сформировать из покрывающего отношения частичного порядка и частичный порядок сам по себе образует отношение достижимости в графе. Если частично упорядоченное множество имеет один минимальный элемент, имеет один максимальный элемент и имеет восходящее планарное представление, оно обязательно формирует решётку, множество, в котором любая пара элементов имеет единственную наибольшую нижнюю границу и единственную наименьшую верхнюю границу. Диаграмма Хассе решётки планарна тогда и только тогда, когда её порядковая размерность не превосходит двух. Однако некоторые частичные порядки размерности два с минимальными и максимальными элементами не имеют восходящего планарного представления (возьмём порядок, определённый транзитивным замыканием порядка $a<b,a<c,b<d,b<e,c<d,c<e,d<f,e<f$).