Теорема Кёнига (комбинаторика)

В теории графов теорема Кёнига (теорема Кёнига-Эгервари, венгерская теорема[1]), доказанная Денешем Кёнигом в 1931[2], утверждает эквивалентность задач нахождения наибольшего паросочетания и наименьшего вершинного покрытия в двудольных графах. Независимо была открыта, в том же 1931[3], Йенё Эгервари[англ.] в несколько более общем виде для случая взвешенных графов.
Определения[править | править код]
Граф называется двудольным, если его вершины можно разбить на два множества так, что у каждого ребра конечные вершины принадлежат разным множествам.
Вершинное покрытие графа — это множество вершин, такое, что любое ребро графа имеет хотя бы одну конечную вершину из этого множества. Вершинное покрытие называется наименьшим, если никакое другое вершинное покрытие не имеет меньшего числа вершин.
Паросочетанием в графе называется множество рёбер, не имеющих общих конечных вершин. Паросочетание называется наибольшим, если никакое другое паросочетание не содержит большего числа рёбер.
Утверждение теоремы[править | править код]
В любом двудольном графе число рёбер в наибольшем паросочетании равно числу вершин в наименьшем вершинном покрытии.
Пример[править | править код]
Двудольный граф на рисунке вверху имеет по 7 вершин в каждой из долей. Паросочетание с 6 рёбрами выделено синим цветом, а вершинное покрытие выделено красным. Это покрытие является наименьшим по размеру, поскольку любая вершина в покрытии должна включать по меньшей мере одну конечную вершину ребра паросочетания. Таким же образом, нет паросочетания большего размера, поскольку любое ребро паросочетания должно содержать по меньшей мере одну конечную вершину из вершинного покрытия, так что это паросочетание является наибольшим. Теорема Кёнига как раз и утверждает равенство размеров паросочетания и покрытия (в данном примере оба числа равны шести).
Доказательства[править | править код]

Доказательство[править | править код]
Пусть задан двудольный граф , а — наибольшее паросочетание в .
Сначала рассмотрим случай, когда паросочетание насыщает все вершины доли , то есть размер паросочетания равен . Очевидно, что вся доля является вершинным покрытием в графе , следовательно, она является и наименьшим вершинным покрытием, и в этом случае утверждение теоремы выполняется.
Иначе возьмём все вершины доли , не насыщенные паросочетанием , и запустим из них обход в ширину по следующему правилу:
- Слева направо переходим только по рёбрам, не входящим в (будем называть их чёрными).
- Справа налево переходим только по рёбрам, входящим в (будем называть их голубыми).
Пусть и — подмножества вершин левой и правой доли, посещённых во время обхода, а и — соответственно, подмножества не посещённых вершин (см. рисунок справа).
Между множествами и нет чёрных рёбер, поскольку иначе во время обхода мы бы посетили вершины из множества . По аналогичной причине, между множествами и нет голубых рёбер.
Докажем, что между множествами и нет также и голубых рёбер. От противного, пусть такое ребро есть. Вершина не могла являться стартовой для обхода в ширину, поскольку она насыщена паросочетанием . Следовательно, обход в ширину пришёл в из какой-то вершины по голубому ребру, что означает, что вершине инцидентны два голубых ребра и . Но это невозможно, поскольку голубые рёбра образуют паросочетание.
Следовательно, любое ребро графа инцидентно или вершине из или вершине из , то есть является вершинным покрытием. Покажем, что все вершины в насыщены паросочетанием . Для вершин из это очевидно, поскольку все ненасыщенные вершины левой доли по построению лежат в . Если в есть ненасыщенная вершина, то существует -чередующая цепь, заканчивающаяся в ней, что противоречит тому, что паросочетание является наибольшим. Теперь осталось вспомнить, что между множествами и нет рёбер из , то есть каждому ребру паросочетания инцидентна в точности одна вершина из вершинного покрытия . Следовательно, , и вершинное покрытие является наименьшим[4].
Доказательство через теорему Форда — Фалкерсона[править | править код]
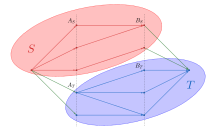
Задача поиска наибольшего паросочетания в графе может быть сведена к нахождению наибольшего потока в транспортной сети , такой что из истока в первую долю и из второй доли в сток проходят рёбра пропускной способности , а для любого ребра исходного графа, из в проходит ребро пропускной способности .
По теореме Форда — Фалкерсона, величина такого потока равна величине минимального разреза в . Пусть такой разрез задан множествами вершин и . Вершины исходного графа можно разбить на четыре группы , такие что и , при том и . При такой классификации, в исходном графе не может быть рёбер из в , так как такие рёбра сделали бы величину разреза бесконечной.
Отсюда, в свою очередь, следует, что любое ребро графа инцидентно вершине из , либо вершине из . В то же время сам разрез составляют рёбра из в и из в . Таким образом, с одной стороны является вершинным покрытием исходного графа, с другой — величина минимального разреза в графе равна , из чего следует, что множество и есть минимальное вершинное покрытие графа [5].
Следствие из теоремы Кёнига[править | править код]
Пусть и — соответственно, наибольшее паросочетание и наименьшее вершинное покрытие в двудольном графе . Тогда любое ребро из инцидентно в точности одной вершине из . И наоборот, любой вершине из инцидентно в точности одно ребро из . Другими словами, отношение инцидентности задаёт биекцию между множествами и .
Заметим, что если бы граф не являлся двудольным, то некоторым рёбрам могли бы быть инцидентны сразу две вершины из , а некоторые вершины из могли бы не иметь инцидентных им рёбер из .
Алгоритм построения наименьшего вершинного покрытия в двудольном графе[править | править код]
Описанный выше обход в ширину из доказательства теоремы строит наименьшее вершинное покрытие по заданному наибольшему паросочетанию.[4] Данный алгоритм имеет сложность . Наибольшее паросочетание в двудольном графе может быть найдено алгоритмом Хопкрофта–Карпа за время .
Связь с совершенными графами[править | править код]
Говорят, что граф совершенен, если для любого порождённого подграфа его хроматическое число равно размеру максимальной клики. Любой двудольный граф совершенен, поскольку любой его подграф является либо двудольным, либо независимым. В двудольном графе, не являющемся независимым, хроматическое число и размер максимальной клики равны двум, в то время как для независимого множества оба этих числа равны единице.
Граф совершенен тогда и только тогда, когда его дополнение совершенно[6], и теорему Кёнига можно считать эквивалентом утверждения, что дополнение двудольного графа совершенно. Любые раскраски дополнения двудольного графа имеют размер максимум 2, а классы размера 2 образуют паросочетания. Клики в дополнении графа — это независимое множество в , и, как мы уже писали выше, независимое множество в двудольном графе — это дополнение вершинного покрытия . Таким образом, любое паросочетание в двудольном графе с вершинами соответствует раскраске дополнения с цветами, что, ввиду совершенства дополнения двудольных графов, соответствует независимому множеству в с вершинами, что соответствует вершинному покрытию вершинами. Следовательно, теорема Кёнига доказывает совершенство дополнений двудольных графов, то есть результат, выраженный в более явной форме у Галлаи[7].
Можно связать также теорему Кёнига о рёберной раскраске с другим классом совершенных графов, рёберными графами двудольных графов. Для графа рёберный граф имеет вершины, соответствующие рёбрам графа , и рёбра для каждой пары смежных рёбер в . Таким образом, хроматическое число равно хроматическому индексу . Если — двудольный, клики в — это в точности множества рёбер в , имеющих общую конечную вершину. Теперь теорема Кёнига о рёберной раскраске, утверждающая, что хроматический индекс равен максимальной степени вершин в двудольном графе, может быть интерпретирована как утверждение, что рёберный граф двудольного графа совершенен.
Поскольку рёберные графы двудольных графов совершенны, дополнения рёберных графов двудольных графов тоже совершенны. Клика в дополнении рёберного графа для — это просто паросочетание . А раскраска дополнения рёберного графа для , в случае, если является двудольным, — это разбиение рёбер графа на подмножества рёбер, имеющих общие вершины. Конечные вершины, являющиеся общими в этих подмножествах, образуют вершинное покрытие графа . Таким образом, сама теорема Кёнига может быть также интерпретирована как утверждение, что дополнение рёберных графов двудольных графов совершенно.
Дополнения[править | править код]
- Для графов, не являющихся двудольными, ситуация с задачами о наибольшем паросочетании и наименьшем вершинном покрытии совсем другая — наибольшее паросочетание можно найти за полиномиальное время для любого графа, в то время как поиск наименьшего вершинного покрытия является NP-полной задачей. Дополнение вершинного покрытия для любого графа — это независимое множество, и поиск наибольшего независимого множества — это ещё одна NP-полная задача.
- Теорема Кёнига эквивалентна массе других минимаксных теорем в теории графов и комбинаторике, таких как теорема Холла о свадьбах и теорема Дилуорса. Поскольку паросочетание в двудольных графах является частным случаем потока в сети, теорема Кёнига также вытекает из теоремы Форда — Фалкерсона.[8]
- В русскоязычном интернете и научной литературе распространена следующая формулировка теоремы: если прямоугольная матрица составлена из нулей и единиц, то минимальное число линий, содержащих все единицы, равно максимальному числу единиц, которые могут быть выбраны так, чтобы никакие две из них не лежали на одной и той же линии (термин «линия» обозначает либо строку, либо столбец в матрице).[9]
- Вопреки эквивалентности двух задач с точки зрения точного решения, они совершенно не эквивалентны для аппроксимационных алгоритмов. Задача о наибольшем паросочетании для двудольных графов может быть аппроксимирована с произвольной точностью за постоянное время с помощью распределённых алгоритмов[англ.], в противоположность задаче о наименьшем вершинном покрытии, требующей как минимум логарифмического времени.[10]
Замечания[править | править код]
- ↑ Эвнин, 2005.
- ↑ Kőnig, 1931.
- ↑ Egerváry, 1931.
- ↑ 1 2 Bondy, 1976, pp. 74-75.
- ↑ Cesa-Bianchi, Nicolò Matchings and the max-flow min-cut theorem (11 апреля 2020). Архивировано 9 мая 2021 года.
- ↑ Ловас, Пламмер, 1998, с. 567.
- ↑ Gallai, 1958.
- ↑ Ловас, Пламмер, 1998, с. 89.
- ↑ Рыбников, 1972, с. 100.
- ↑ Göös, 2012.
Ссылки[править | править код]
- Ловас Л., Пламмер М. Прикладные задачи теории графов. Теория паросочетаний в математике, физике, химии. — М.: Мир, 1998. — 653 с. — ISBN 5-03-002517-0.
- Рыбников К.А. Введение в комбинаторный анализ. — МГУ, 1972.
- Эвнин А. Ю. Вокруг теоремы Холла // Матем. обр.. — 2005. — Т. 3(34). — С. 2—23.
- Bondy, J. A., Murty, U. S. R. Graph Theory with Applications. — North Holland, 1976. — ISBN 0-444-19451-7.
- Egerváry, Jenő. Matrixok kombinatorius tulajdonságairól [On combinatorial properties of matrices] (венг.) // Matematikai és Fizikai Lapok. — 1931. — Vol. 38. — P. 16-28.
- Gallai, Tibor. Maximum-minimum Sätze über Graphen // Acta Math. Acad. Sci. Hungar.. — 1958. — Vol. 9. — Вып. 3-4. — P. 395–434. — doi:10.1007/BF02020271.
- Göös, Mika. Jukka Suomela. 26th International Symposium on Distributed Computing (DISC), Salvador, Brazil, October 2012. — 2012.
- Kőnig, Dénes. Gráfok és mátrixok (венг.) // Matematikai és Fizikai Lapok. — 1931. — Vol. 38. — P. 116–119.
Для улучшения этой статьи желательно:
|















































