Алгоритм Коэна — Сазерленда
Алгоритм Коэна — Сазерленда (англ. Cohen–Sutherland) — алгоритм отсечения отрезков, то есть алгоритм, позволяющий определить часть отрезка, которая пересекает прямоугольник. Был разработан Дэном Коэном и Айвеном Сазерлендом в Гарварде в 1966—1968 гг., и опубликован на конференции AFIPS в 1968[1][2].
Описание алгоритма[править | править код]
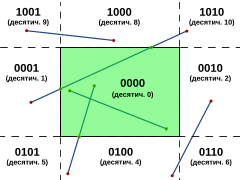
Алгоритм разделяет плоскость на 9 частей прямыми, которые образуют стороны прямоугольника. Каждой из 9 частей присваивается четырёхбитный код. Биты (от младшего до старшего) значат «левее», «правее», «ниже», «выше». Иными словами, у тех трёх частей плоскости, которые слева от прямоугольника, младший бит равен 1, и так далее.
Алгоритм определяет код концов отрезка. Если оба кода равны нулю, то отрезок полностью находится в прямоугольнике. Если битовое И кодов не равно нулю, то отрезок не пересекает прямоугольник (так как это значит, что оба конца отрезка находятся с одной стороны прямоугольника). В прочих случаях, алгоритм выбирает конец отрезка (или один из концов), имеющий ненулевой код (то есть находящийся вне прямоугольника), находит ближайшую к нему точку пересечения отрезка с одной из прямых, образующих стороны прямоугольника, и использует эту точку пересечения как новый конец отрезка. Укороченный отрезок снова пропускается через алгоритм.
Реализация алгоритма для трёхмерной модели идентична двумерной реализации, за исключением того, что вместо четырёхразрядного кода применяется шестиразрядный (дополнительные два бита глубины).
См. также[править | править код]
Примечания[править | править код]
- ↑ A Critical History of Computer Graphics and Animation. Section 4: Basic and applied research moves the industry (англ.). Дата обращения: 26 февраля 2009. Архивировано 27 марта 2012 года.
- ↑ Robert F. Sproull, Ivan E. Sutherland. A clipping divider // AFIPS Joint Computer Conferences : Proceedings of the December 9-11, 1968, fall joint computer conference. — New York: ACM, 1968. — Т. I. — С. 765—775.
Для улучшения этой статьи желательно:
|