Граф Леви

Граф Ле́ви
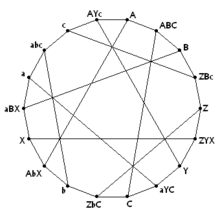Граф Паппа — граф Леви с 18 вершинами, образованный из конфигурации Паппа. Вершины, помеченные одной буквой, соответствуют точкам в конфигурации. Вершины, помеченные тремя буквами, соответствуют прямым, проходящим через три точки.
Обхват	≥ 6

Граф Ле́ви (также граф инциде́нтности) — двудольный граф, соответствующий структуре инцидентности. Из набора точек и линий в геометрии инцидентности или проективной конфигурации образуется граф с одной вершиной для каждой точки, одной вершиной для каждой линии и одного ребра для каждой инциденции точки и линии (то есть отношения «точка лежит на линии»). Эти графы назвали именем Фридриха Леви, который описал их в 1942 году.

Граф Леви системы точек и линий обычно имеет обхват по меньшей мере шесть: любой цикл длины 4 должен соответствовать двум линиям, проходящим через те же самые две точки. Следовательно, любой двудольный граф с обхватом по меньшей мере шесть можно рассматривать как граф Леви абстрактной структуры инцидентности. Графы Леви конфигураций являются бирегулярными и любой бирегулярнй граф с обхватом как минимум шесть можно рассматривать как граф Леви абстрактной конфигурации.

Графы Леви можно также определить для других типов структур инциденций, таких как инциденции между точками и плоскостями в евклидовом пространстве. Для любого графа Леви существует эквивалентный гиперграф и наоборот.

Примеры

• Граф Дезарга является графом Леви конфигурации Дезарга, состоящей из 10 точек и 10 прямых. На каждой прямой находятся 3 точки и 3 прямых проходят через каждую точку. Граф Дезарга можно рассматривать также, как обобщённый граф Петерсена G (10,3) или как двудольный граф Кнезера с параметрами 5,2. Он является 3-регулярным графом с 20 вершинами.

• Граф Хивуда является графом Леви плоскости Фано. Известен также как (3,6)-клетка и является 3-регулярным графом с 14 вершинами.

• Граф Мёбиуса — Кантора является графом Леви конфигурации Мёбиуса — Кантора, системы из 8 точек и 8 линий, которые нельзя реализовать с помощью прямых линий на евклидовой плоскости. Он является 3-регулярным графом и имеет 16 вершин.

• Граф Паппа является графом Леви конфигурации Паппа, состоящей из 9 точек и 9 прямых. Как и в конфигурации Дезарга, на каждой прямой находятся 3 точки и через каждую точку проходят 3 прямые. Граф является 3-регулярным и имеет 18 вершин.

• Граф Грея является графом Леви конфигурации, которую можно получить в R³ как 3×3×3 решётку 27 точек и 27 ортогональных прямых, проходящих через эти точки.

• 8-клетка Татта является графом Леви конфигурации Кремоны — Ричмонда. Граф известен также как (3,8)-клетка, является 3-регулярным и имеет 30 вершин.

• Граф четырёхмерного гиперкуба Q₄ является графом Леви конфигурации Мёбиуса, образованной точками и плоскостями двух взаимно вписанных тетраэдров. Здесь тетраэдр считается вписанным в другой, если все его вершины лежат на плоскостях, проходящих через грани другого тетраэдра (не обязательно на самих гранях).

• Граф Любляны с 112 вершинами является графом Леви конфигурации Любляны.

Ссылки

• Weisstein, Eric W. Levi Graph (англ.) на сайте Wolfram MathWorld.