Граф Любляны
| Граф Любляны | |
|---|---|
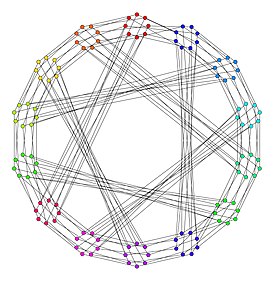 Граф Любляны как накрывающий граф графа Хивуда | |
| Вершин | 112 |
| Рёбер | 168 |
| Радиус | 7 |
| Диаметр | 8 |
| Обхват | 10 |
| Автоморфизмы | 168 |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Свойства |
Кубический Гамильтонов Полусимметричный |
Граф Любляны — неориентированный двудольный граф с 112 вершинами и 168 рёбрами[1].
Граф является кубическим графом с диаметром 8, радиусом 7, хроматическим числом 2 и хроматическим индексом 3. Его обхват равен 10 и в нём есть ровно 168 циклов длины 10. Есть также 168 циклов длины 12[2].
Построение
[править | править код]Граф Любляны гамильтонов и может быть построен из LCF-кода : [47, -23, -31, 39, 25, -21, -31, -41, 25, 15, 29, -41, -19, 15, -49, 33, 39, -35, -21, 17, -33, 49, 41, 31, -15, -29, 41, 31, -15, -25, 21, 31, -51, -25, 23, 9, -17, 51, 35, -29, 21, -51, -39, 33, -9, -51, 51, -47, -33, 19, 51, -21, 29, 21, -31, -39]2.
Граф Любляны является графом Леви конфигурации Любляны, конфигурации без четырёхугольников с 56 прямыми и 56 точками[2]. В этой конфигурации каждая прямая содержит в точности 3 точки, каждая точка принадлежит в точности 3 прямым и любые две прямые пересекаются максимум в одной точке.
Алгебраические свойства
[править | править код]Группа автоморфизмов графа Любляны является группой порядка 168. Она действует транзитивно на рёбрах, но не на вершинах — есть симметрии, переводящие любое ребро в любое другое ребро, но нет симметрии, переводящей любую вершину в любую другую вершину. Поэтому граф Любляны является полусимметричным графом, третьим по счёту кубическим полусимметричным графом после графа Грея с 54 вершинами и графа Иванова — Иофиновой с 110 вершинами[3].
Характеристический многочлен графа Любляны равен
История
[править | править код]Граф Любляны впервые опубликовали в 1993 году Брауэр, Деджтер и Томассен[4] как самодополнительный подграф графа Деджтера[5].
В 1972 году Брауэр уже говорил о 112-вершинном рёберно транзитивном, но не вершинно транзитивном, кубическом графе, найденном Фостером, однако не опубликованном[6]. Кондер, Малнич, Марушич и Поточник заново открыли этот 112-вершинный граф в 2002 году и назвали его графом Любляны по имени столицы Словении[2]. Они доказали, что граф был единственным 112-вершинным рёберно транзитивным, но не вершинно транзитивным, кубическим графом, а потому это тот самый граф, который нашёл Фостер.
Галерея
[править | править код]-
Граф Любляны является гамильтоновым и двудольным.
-
Хроматический индекс графа Любляны равен 3.
-
Альтернативный рисунок графа Любляны.
-
Граф Любляны является графом Леви этой конфигурации.
Примечания
[править | править код]- ↑ Weisstein, Eric W. Ljubljana Graph (англ.) на сайте Wolfram MathWorld.
- ↑ 1 2 3 Conder, Malnič, Marušič, Pisanski, Potočnik, 2002.
- ↑ Conder, Malnič, Marušič, Potočnik, 2006, с. 255—294.
- ↑ Brouwer, Dejter, Thomassen, 1993, с. 25—29.
- ↑ Klin, Lauri, Ziv-Av, 2012, с. 1175–1191.
- ↑ Bouwer, 1972, с. 32—40.
Литература
[править | править код]- Marston Conder, Aleksander Malnič, Dragan Marušič, Primož Potočnik. A census of semisymmetric cubic graphs on up to 768 vertices // Journal of Algebraic Combinatorics. — 2006. — Т. 23. — С. 255–294. — doi:10.1007/s10801-006-7397-3.
- Brouwer A. E., Dejter I. J., Thomassen C. Highly Symmetric Subgraphs of Hypercubes // J. Algebraic Combinat.. — 1993. — Вып. 2.
- Klin M., Lauri J., Ziv-Av M. Links between two semisymmetric graphs on 112 vertices through the lens of association schemes // Jour. Symbolic Comput.. — 2012. — Т. 7, вып. 10.
- Bouwer I. Z. On Edge But Not Vertex Transitive Regular Graphs // J. Combin. Th. Ser. B. — 1972. — Вып. 12.
- Conder M., Malnič A., Marušič D., Pisanski T., Potočnik P. The Ljubljana Graph // IMFM Preprints. — Ljubljana: Institute of Mathematics, Physics and Mechanics, 2002. — Т. 40, вып. 845.
Для улучшения этой статьи желательно:
|




