Обсуждение:Дерево (теория графов)
Проект «Математика» (уровень III, важность для проекта высокая)
Эта статья тематически связана с вики-проектом «Математика», цель которого — создание и улучшение статей по темам, связанным с математикой. Вы можете её отредактировать, а также присоединиться к проекту, принять участие в его обсуждении и поработать над требуемыми статьями. |
Untitled[править код]
Предлагаю переименовать эту статью с «Дерево» на «Дерево (теория графов)». А в статье «Дерево» сделать ссылки на другие значения термина.
Такое нет смысла делать пока не пояжились другие статьи --Tosha 14:29, 12 июля 2005 (UTC)
- Мне кажется, есть. Даже две причины.
- не придется потом переделывать ссылки на эту статью
- есть много ссылок, не относящихся к теории графов и они сейчас синие, а должны быть красными
- Предлагаю сделать «Дерево (теория графов)» и «Дерево (значения)».
- SergV 18:05, 17 июля 2005 (UTC)
Да, ты прав, большинство ссылок не туда. --Tosha 21:44, 22 июля 2005 (UTC)
Интересная ассимптотика числа неизоморфных деревьев. Хорошо бы вставить ссылку на автора. Нет ли получше нижних оценок на число неизоморфных корневых? Олег.
- Otter, Ann.Math. 1948 v.49 №3, p.583-99, ссылка из МатЭнциклопедии --Tosha 02:20, 18 сентября 2005 (UTC)
Цитата: "висячая вершина — это вершина степени 1. Листом дерева называется любая его висячая вершина (вместе с соотв. ребром)." В таком случае под определение листа тут подойдет корень, если у него один потомок,а это бред.
Теорема Кэли.[править код]
Тоша, не стоит ли добавить какую-нибудь ссылку (сноской) про теорему Кэли, для более быстрой, нежели "пойти в библиотеку", проверяемости (да и вообще иметь возможность быстро посмотреть, "откуда оно", для потенциального читателя было бы неплохо)? Я навскидку могу вспомнить записки дубнинского курса Бурмана тут, но а) это просто записки лекций и б) сам я их добавить не могу, ибо нахожусь в конфликте интересов: я слишком тесно с этой школой связан. Burivykh 23:13, 28 октября 2009 (UTC)
- Посмотрел -- наверное, не стоит: нарушится баланс статьи. А вот если делать отдельную статью (теорема Кэли плюс числа Гурвица плюс многочлены плюс накрытия), тогда, наверное, можно будет и сослаться. Эх. Ещё одно TODO. :) Burivykh 23:16, 28 октября 2009 (UTC)
- О, нашёл независимую ссылку. Правда, там по-другому (не через связь с многочленами и накрытиями), но для одного подтверждения этого достаточно, а двух разных взглядов в статье не специально о теореме Кэли не надо. Burivykh 11:33, 29 октября 2009 (UTC)
Иллюстрация к двоичному дереву[править код]
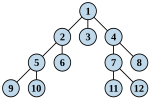
Коллеги, картинка-иллюстрация была убрана с комментарием, что это не двоичное дерево. Формально, конечно, степень корня ровно 3, а дерево неориентировано — но оно нарисовано так, что его очень естественно ориентировать «сверху вниз», а тогда оно под определение не подпадает. То есть — действительно, лучше эту картинку не использовать. Кто-нибудь может нарисовать более «каноническую» иллюстрацию? --Burivykh 07:00, 23 января 2011 (UTC)
- Добавил иллюстрацию из АнглВики. Petrohan 12:03, 23 января 2011 (UTC)
Связанные определения[править код]
Первое определение вступает в противоречие со вторым. """ Степень узла — количество исходящих дуг (или, иначе, количество поддеревьев узла). Концевой узел (лист, терминальная вершина) — узел со степенью 1 (то есть узел, в который ведёт только одно ребро; в случае ориентированного дерева — узел, в который ведёт только одна дуга и не исходит ни одной дуги). """
Во втором следует написать «узел со степенью 0»? 212.122.7.19 17:57, 2 июня 2015 (UTC) Антон
В английской версии статьи: "A leaf is a vertex of degree 1". Частично поправил, про степень вершины. 79.133.114.37 21:34, 16 июля 2015 (UTC) 79.133.114.37 21:20, 16 июля 2015 (UTC)
