Оконное преобразование Фурье
Оконное преобразование Фурье — это разновидность преобразования Фурье, определяемая следующим образом:
где — некоторая оконная функция. В случае дискретного преобразования оконная функция используется аналогично:
Существует множество математических формул, визуально улучшающих частотный спектр на разрыве границ окна. Для этого применяются преобразования: треугольное (Барлетта), синус-окно, синус в кубе, синус в 4-й степени, преобразование Парзена, Уэлча, Гаусса, Хеннинга, приподнятый косинус (Хэмминга), Чебышева, с пульсациями, Розенфилда, Блэкмана-Харриса, горизонтальное и с плоской вершиной. Также существует методика по взаимному перекрытию окон, при этом обычно можно выбрать сколько семплов из предыдущего окна будет усреднено с текущим окном.
Применение[править | править код]
На практике нет возможности получить сигнал на бесконечном интервале, так как нет возможности узнать, какой был сигнал до включения устройства и какой он будет в будущем. Ограничение интервала анализа равносильно произведению исходного сигнала на прямоугольную оконную функцию. Таким образом, результатом оконного преобразования Фурье является не спектр исходного сигнала, а спектр произведения сигнала и оконной функции. В результате возникает эффект, называемый растеканием спектра сигнала. Опасность заключается в том, что боковые лепестки сигнала более высокой амплитуды могут маскировать присутствие других сигналов меньшей амплитуды.
Для борьбы с растеканием спектра применяют более гладкую оконную функцию, спектр которой имеет более широкий главный лепесток и низкий уровень боковых лепестков. Спектр, полученный при помощи оконного преобразования Фурье, является сверткой спектра исходного идеального сигнала и спектра оконной функции.
Искажения, вносимые применением окон, определяются размером окна и его формой. Выделяют следующие основные свойства оконных функций: ширина главного лепестка по уровню -3 дБ, ширина главного лепестка по нулевому уровню, максимальный уровень боковых лепестков, коэффициент ослабления оконной функции.
Оконное преобразование Фурье применяется в связи для синтеза частотных фильтров, например, в методе частотного мультиплексирования с множеством несущих, использующим банк (гребёнку) частотных фильтров FBMC[1].
Частотно-временное разрешение[править | править код]
При использовании оконного преобразования Фурье невозможно одновременно обеспечить хорошее разрешение по времени и по частоте. Чем уже окно, тем выше разрешение по времени и ниже разрешение по частоте.
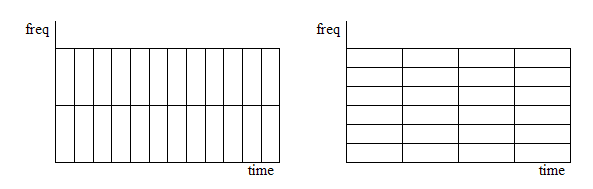
Разрешение по осям является постоянным. Это нежелательно для ряда задач, в которых информация по частотам распределена неравномерно. В таких задачах в качестве альтернативы оконному преобразованию Фурье может использоваться вейвлет-преобразование, временное разрешение которого увеличивается с частотой (частотное снижается).
Типы оконных функций[править | править код]
Прямоугольное окно[править | править код]

Получается автоматически при ограничении выборки N отсчетами. Максимальный уровень боковых лепестков частотной характеристики: -13 дБ.
Окно Ханна (Хеннинга)[править | править код]

где N — ширина окна. Уровень боковых лепестков: −31.5 дБ.
Окно Хэмминга[править | править код]

Уровень боковых лепестков: -42 дБ.
Окно Блэкмана[править | править код]

Уровень боковых лепестков: -58 дБ (α=0.16).
Окно Кайзера[править | править код]


где — модифицированная функция Бесселя первого рода нулевого порядка; — коэффициент определяющий долю энергии, сосредоточенной в главном лепестке спектра оконной функции. Чем больше тем больше доля энергии, и шире главный лепесток, и меньше уровень боковых лепестков. На практике используются значения от 4 до 9.
Реализация[править | править код]
Для оконного преобразования Фурье в цифровом виде может применяться не только взвешивание каждого цифрового отсчета в процессе формирования свертки, но и эквивалентное весовое суммирование откликов преобразования Фурье[1].
К примеру взвешивание окном Ханна (Хеннинга) и окном Хэмминга может быть представлено в виде:
- ,
где , , - исходные отклики преобразования Фурье, - результат оконного преобразования, соответствует окну Ханна (Хеннинга), - окну Хэмминга[1][2].
Реализация указанного взвешивания осуществляется в режиме скользящего окна по массиву откликов преобразования Фурье.
См. также[править | править код]
Примечания[править | править код]
- ↑ 1 2 3 Слюсар В.И. Современные тренды радиорелейной связи. //Технологии и средства связи. – 2014. - № 4. - С. 32 - 36. [https://web.archive.org/web/20200110062028/https://slyusar.kiev.ua/TSS_4_2014_1.pdf Архивная копия от 10 января 2020 на Wayback Machine]
- ↑ Слюсар В. И., Королев Н. А. Ващенко П. А. Метод повышения частотной избирательности систем сотовой связи, использующих цифровое диаграммообразование. // Тезисы докладов ХІV НТК. Часть 1. - Житомир: ЖВИРЭ. - 2004. - С. 77. [1] Архивная копия от 14 января 2020 на Wayback Machine


![{\displaystyle F(m,\omega )=\sum _{n=-\infty }^{\infty }f[n]w[n-m]e^{-j\omega n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34e875850d9c1082c0170af8727ebaf07164302f)
![{\displaystyle w(n)=\left\{{\begin{matrix}1,&n\in [0,N-1]\\0,&n\notin [0,N-1]\\\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e8c05251e31de24a675a681e81e1ad09721c839)













