Релятивистская квантовая химия

Релятивистская квантовая химия — раздел квантовой химии, использующий понятия из области квантовой механики и теории относительности для объяснения и предсказания свойств и структур соединений или атомов. Речь идёт об атомах, электроны которых имеют характерные скорости движения близкие к скорости света (0,2 с и выше). Примером могут служить атомы тяжёлых и сверхтяжёлых элементов.

Первоначально квантовая механика была разработана без учёта теории относительности. «Релятивистскими эффектами» являются расхождения между значениями, рассчитанными с помощью моделей с учётом и без учёта теории относительности. Релятивистские эффекты имеют важное значение для элементов с большими атомными номерами. Например, для лантаноидов и актиноидов.

История

Начиная с 1935 года, Берта Свелс провела релятивистское описание многоэлектронных систем, вопреки сделанному в 1929 году Полем Дираком заявлению, что единственные недостатки, остающиеся в квантовой механике «… приводят к возникновению трудностей только тогда, когда задействованы высокоскоростные частицы, и поэтому не имеют значения при рассмотрении строения атомов и молекул и обычных химических реакций, в которых обычные квантово-механические расчёты, как правило, достаточно точны, если пренебречь релятивистским изменением массы и скорости, и принимать в расчёт только кулоновское взаимодействие между электронами и атомными ядрами».

Химики-теоретики в целом соглашались с заявлением Дирака вплоть до 1970-х годов, когда появились работы, которые показали реализацию релятивистских эффектов в соединениях тяжёлых элементов. Уравнение Шрёдингера в оригинальной статье 1926 года не учитывала теорию относительности. Релятивистские поправки к уравнению были сделаны позже (см. уравнения Клейна-Гордона-Фока), чтобы объяснить тонкую структуру атомных спектров. Однако эти и другие поправки к уравнению Шрёдингера не сразу получили распространение в химическом сообществе. Поскольку атомные спектры разрабатывались в значительной степени в области физики, а не химии, большинство химиков не были знакомы с релятивистской квантовой механикой, а их внимание было сосредоточено на свойствах более лёгких элементов.

Мнение Дирака о роли релятивистских эффектов для квантовой химии оказалось ошибочным по двум причинам:

• электроны s- и р-орбиталей движутся со значительной долей скорости света, если боровский радиус и заряд ядра достаточно велики
• существуют косвенные последствия релятивистских эффектов, которые особенно заметны для d- и f-атомных орбиталей.

Качественное описание

Зависимость от скорости электрона (горизонтальная ось) выраженности релятивистской поправки (вертикальная ось) к массе электрона. При малой скорости $E_{rel}$ (ордината) равна $E_{0}=mc^{2}$. Однако при $v_{e}\to c$ параметр $E_{rel}$ стремится к бесконечности

Одним из наиболее важных и известных результатов релятивистской механики является то, что релятивистская масса электрона увеличивается

$m_{rel}={\frac {m_{e}}{\sqrt {1-(v_{e}/c)^{2}}}}$

где $\displaystyle m_{e},v_{e},c$ — масса покоя электрона, скорость электрона и скорость света соответственно. Рисунок справа иллюстрирует изменение релятивистской массы электрона в зависимости от его скорости. Изменение массы электрона непосредственно влияет на боровский радиус $\displaystyle a_{0}$ этого электрона

$a_{0}={\frac {\hbar }{m_{e}c\alpha }}$

где $\hbar$ — приведённая постоянная Планка, а α — постоянная тонкой структуры (релятивистская поправка к модели Бора)

Арнольд Зоммерфельд подсчитал, что для 1s-электрона атома водорода орбитальный радиус 0,0529 нм и α ≈ 1/137. То есть, такой электрон движется почти с 1/137 скорости света. Можно распространить этот результат на более сложные электронные системы, используя для грубой оценки вклада релятивистских эффектов формулу v ≈ Zc/137 для 1s-электрона, где v является радиальной скоростью этого электрона, Z — заряд ядра (или порядковый номер элемента в таблице Менделеева), а с — скорость света. Например, для золота (Z = 79) получается результат α = 0,58c — то есть он имеет скорость, близкую к 58 % скорости света. Подставляя это в отношение v/c для расчёта релятивистской массы, получаем m_rel = 1.22m_e. Используя это для оценки боровского радиуса $\displaystyle a_{0}$, получаем, что он изменяется на 22 % по сравнению с нерялитивистским радиусом для такого же электрона.

Если подставить в уравнение для релятивистской массы радиус Бора, то можно записать

$a_{rel}={\frac {\hbar {\sqrt {1-(v_{e}/c)^{2}}}}{m_{e}c\alpha }}$

тогда

${\frac {a_{rel}}{a_{0}}}={\sqrt {1-(v_{e}/c)^{2}}}$

Рисунок справа показывает, как изменяется отношение релятивистского радиуса Бора к нерелятивистскому в зависимости от скорости электрона. Обратите внимание на то, что релятивистская модель предсказывает уменьшение радиуса с увеличением скорости.

Отношение релятивистского боровского радиуса атома к нерелятивистскому как функция скорости внешних электронов

Когда боровское описание распространяется на водородоподобные атомы с помощью квантового правила, радиус Бора становится

$r={\frac {n^{2}\hbar ^{2}4\pi \epsilon _{0}}{m_{e}Ze^{2}}}$

где $n$ — главное квантовое число, а Z — атомный номер. В квантовой механике момент импульса описывается как $mv_{e}r=n\hbar$. Если подставить это в уравнение выше, то для $v$ получается выражение

$r={\frac {mv_{e}rn\hbar 4\pi \epsilon _{0}}{mZe^{2}}}$

$1={\frac {v_{e}n\hbar 4\pi \epsilon _{0}}{Ze^{2}}}$

$v_{e}={\frac {Ze^{2}}{n\hbar 4\pi \epsilon _{0}}}$

Используя атомную систему единиц, можно упростить выражение

$v_{e}={\frac {Z}{n}}$

Подставляя это в приведённое выше отношение Бора, получаем

${\frac {a_{rel}}{a_{0}}}={\sqrt {1-\left({\frac {Z}{nc}}\right)^{2}}}$

При низком значении $n$ и высоком значении $Z$ будет ${\frac {a_{rel}}{a_{0}}}<1$. Это интуитивно понятно: электроны с более низкими главными квантовыми числами будет иметь более высокую плотность вероятности нахождения у ядра. Ядро с большим зарядом придаёт электронам более высокую скорость (кулоновское взаимодействие прямо пропорционально величине заряда). Более высокая скорость означает повышенную релятивистскую массу, в результате чего такие электроны будут больше времени находиться вблизи ядра (в квантовой механике полная энергия электрона обратно пропорциональна массе электрона и прямо пропорциональна характерному расстоянию электрона от ядра) и тем самым понижают эффективный радиус орбиталей этих электронов.

Влияние на периодичность свойств элементов

Многие из химических и физических различий между 6-м периодом (Cs-Rn) и 5-м периодом (Rb-Xe) возникают из значительных релятивистских эффектов для элементов 6-го периода. Большой заряд ядра и одновременная удаленность электронов от него (на внешних оболочках) заставляет последних двигаться с околосветовыми скоростями. Эти релятивистские эффекты особенно велики для золота, платины и ртути.

Ртуть

Ртуть (Hg) имеет температуру плавления Т_пл.= −39 °C. Связи между атомами ртути Hg-Hg в её кристаллической решётке слабее, чем в простых веществах соседних с ней элементов — кадмия (Т_пл.=321 °C) и золота (Т_пл.=1064 °C). Лантаноидное сжатие даёт только частичное объяснение этой аномалии. В отличие от многих металлов, в газовой фазе ртуть также обнаруживается в одноатомной форме Hg(g). Также в газовой фазе обнаруживаются и стабильные частицы вида Hg₂²⁺(g). Перечисленные три свойства могут быть объяснены исходя из релятивистских свойств внешних электронных оболочек атомов ртути.

Hg₂(g) не формируется потому, что 6s²-орбиталь сжимается благодаря релятивистскому эффекту и из-за этого мало подходит для образования каких-либо связей с другими атомами; на самом деле Hg-Hg соединение должно быть в основном результатом ван-дер-ваальсовых сил, что объясняет, почему взаимодействие Hg-Hg достаточно слабое, чтобы позволить ртути быть жидкостью при комнатной температуре.

Разница между Au₂(g) и Hg(g) сходна с разницей между H₂(g) и He(g). Релятивистское сжатие 6s²-орбитали меняет свойства ртути таким образом, что газообразная ртуть может быть названа «псевдо-благородным газом».

Цвет золота и цезия

Кривые спектральной отражательной способности для алюминиевого (Al), серебряного (Ag) и золотого (Au) металлических покрытий (зеркал)

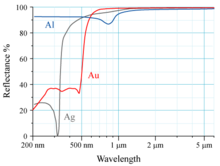
Отражательные свойства Au, Ag, Al показаны на рисунке справа. Человеческий глаз видит электромагнитное излучение с длиной волны около 600 нм как жёлтый свет. Как видно из его спектра отражения, золото кажется жёлтым, так как оно поглощает синий свет больше, чем другие видимые длины волн света. В отражённом свете (который и определяет то, что мы видим) меньше представлена синяя часть оптического спектра.

Поглощение света происходит за счёт электронного перехода 5d --> 6s уровня. Аналогичный переход происходит и в случае Ag, но релятивистские эффекты ниже для Ag. Несмотря на небольшое сжатие 4d- и 5s-орбиталей, расстояние (разница энергий) между ними для Ag по-прежнему намного больше, чем 5d-6s расстояния у Au, так как релятивистские эффекты в последнем случае значительно сильнее. Таким образом, нерелятивистское золото будет белым. Релятивистские эффекты обеспечивают повышение энергии 5d-орбитали и снижение энергии 6s-орбитали.

Аналогичный эффект имеет место для цезия. В то время как другие щелочные металлы серебристо-белые, цезий имеет ярко выраженный золотистый оттенок.

Прочие явления

Другие явления, обычно объясняемые с помощью релятивистских эффектов:

• Существование фторида ртути (IV)
• Аурофильность
• Кристаллическая структура свинца (ГЦК вместо алмазоподобной)
• Поразительное сходство между цирконием и гафнием
• Небольшие атомные радиусы франция и радия
• Около 10 % лантаноидного сжатия объясняется релятивистской поправкой к массе электрона
• Для некоторых элементов (например, золото-79 — которое почти вдвое плотнее, чем свинец-82) значительно больше 10 % сжатия объясняется релятивистской поправкой

Влияние на структуру соединений

С помощью релятивистских эффектов объясняют стабильность анионов «благородных» металлов в таких соединениях, как

• аурид цезия
• платиниды цезия и бария
• Стабильность катиона уранила, а также катионов соседних с ураном актиноидов (Pa-Am) в высоких степенях окисления
• Повышение степени ковалентности связей M-L (металл-неметалл) в соединениях трансактиниевых элементов. На примере соединений вида ML₅ четырёх элементов, показано, что ковалентность связей повышается в результате понижения эффективного заряда на атомах металла и повышения заселённости связывающих орбиталей.

Литература

• Мотт Н, Снеддон И. «Волновая механика и её применения». — М.:Наука, 1966. — 430 с.
• Зайцевский А. В. «Релятивистская теория строения молекул». — М.: Изд-во МГУ, 2005. — 93 с.
• Kaldor, U.; Wilson, Stephen «Theoretical Chemistry and Physics of Heavy and Superheavy Elements» — Dordrecht, Netherlands: Kluwer Academic Publishers, 2003.
• Liu W. «Handbook of Relativistic Quantum Chemistry» — Springer, 2017. — 907 p. — ISBN 978-3-642-40766-6; 978-3-642-40765-9
• De Jong W.A. «Relativistic Quantum Chemistry Applied» — Wibe Albert de Jong, 1997. — 159 p.
• Dyall K.G., Knut F. «Introduction to relativistic quantum chemistry» — Oxford University Press, 2007. — 545 p.
• Hess B.A. «Relativistic effects in heavy-element chemistry and physics» — John Wiley & Sons Ltd, 2003. — 301 p.
• Reiher M., Wolf A. «Relativistic Quantum Chemistry. The Fundamental Theory of Molecular Science» — Wiley-VCH, 2014. — 765 p.