Трансверсальность

Трансверсальное пересечение.

Нетрансверсальное пересечение.

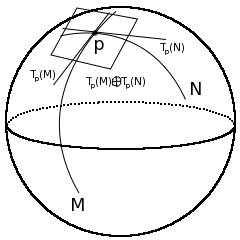
Трансверсальность — условие общего положения на пересечение гладких многообразий. Иногда используется обозначение

$M\pitchfork N$

для трансверсально пересекающихся подмногообразий $M$ и $N$.

Определение

Два гладких подмногообразия $M$ и $N$, вложенные в объемлющее пространство $S$, пересекаются трансверсально в точке $p$, если соответствующие касательные пространства $T_{p}(M)$ и $T_{p}(N)$ порождают всё касательное пространство объемлющего многообразия в точке $p$, то есть $T_{p}(M)+T_{p}(N)=T_{p}(S)$.

Свойства

• Условие трансверсальности пересечения является условием общего положения. То есть, если даны два произвольных гладких подмногообразия $M$ и $N$, то произвольно малой гладкой деформацией $N$ можно добиться того, чтобы многообразия пересекались трансверсально в любой точке их пересечения.
  • В частности, если суммарная размерность $M$ и $N$ строго меньше чем размерность объемлющего пространства, то после произвольно малой деформации можно добиться того, что подмногообразия не имеют точек пересечения.

Литература

• Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия: Методы и приложения. — М.: Наука, 1979.