Теорема о шести окружностях: различия между версиями
| [отпатрулированная версия] | [отпатрулированная версия] |
→Вариации и обобщения: Пишем по-русски и по фактам. Хотя, возможно, последнее предложение получилось слишком длинным. |
|||
| Строка 12: | Строка 12: | ||
;Теорема о семи окружностях |
;Теорема о семи окружностях |
||
Проведём цепочку из шести черных окружностей (см. рис. справа), каждая из которых касается седьмой окружности (красная) и двух соседних окружностей. Тогда три линии (синие), проведенные между противоположными парами точек касания с седьмой окружностью, пересекаются в одной точке (зеленая). Эта элементарная по сути теорема не была известна вплоть до 1974 года <ref>Evelyn, C. J. A.; Money-Coutts, G. B.; and Tyrrell, J. A. "The Seven Circles Theorem." §3.1 in The Seven Circles Theorem and Other New Theorems. London: Stacey International, pp. 31-37, 1974.</ref><ref>Seven circles theorem. Теорема о шести окружностях (англ. яз.)// https://en.wikipedia.org/wiki/Seven_circles_theorem</ref>. |
|||
Подобрав радиусы трёх окружностей соответствующим образом (и выставив окружности наружу), можно получить прямые вместо трёх оставшихся окружностей. Эти прямые образуют треугольник, а все четыре нарисованные окружности будут создавать ситуацию с последнего рисунка среди четырёх примеров к основной теореме, где также видны три чевианы к точкам касания окружностей и прямых, пересекающиеся в одной точке. |
|||
Если радиусы трёх окружностей приблизятся к бесконечности, три окружности превратятся в прямые линии — в стороны треугольника, а центральная окружность — во вписанную окружность этого треугольника. Тогда три линии, соединяющие противоположные точки касания (точки касания со сторонами образованного треугольника с соответствующими противоположными им вершинами треугольника), также пересекутся в одной точке (как чевианы треугольника). Это соответствует последнему рисунку справа внизу, где, кстати, видны и три указанные чевианы, пересекающиеся в одной точке. |
|||
== См. также == |
== См. также == |
||
Версия от 07:42, 21 мая 2020

Теорема о шести окружностях — теорема в геометрии треугольника.
Формулировка
Рассмотрим цепь из окружностей, каждая из которых касается двух сторон данного треугольника, а также предыдущей окружности в цепи. Тогда эта цепь замыкается, в том смысле, что шестая окружность касается первой[1].
Вариации и обобщения
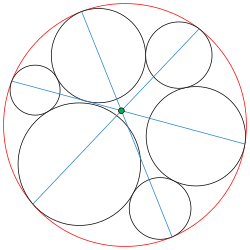
- Теорема о семи окружностях
Проведём цепочку из шести черных окружностей (см. рис. справа), каждая из которых касается седьмой окружности (красная) и двух соседних окружностей. Тогда три линии (синие), проведенные между противоположными парами точек касания с седьмой окружностью, пересекаются в одной точке (зеленая). Эта элементарная по сути теорема не была известна вплоть до 1974 года [2][3].
Подобрав радиусы трёх окружностей соответствующим образом (и выставив окружности наружу), можно получить прямые вместо трёх оставшихся окружностей. Эти прямые образуют треугольник, а все четыре нарисованные окружности будут создавать ситуацию с последнего рисунка среди четырёх примеров к основной теореме, где также видны три чевианы к точкам касания окружностей и прямых, пересекающиеся в одной точке.
См. также
- Окружности Мальфатти
- Окружность Форда
- Поризм Штейнера
- Поризм Понселе
- Цепь Паппа Александрийского
- Цепь Понселе
- Лемма о шестой окружности
- Теорема Микеля о шести окружностях
- Теорема о пяти кругах
Примечания
- ↑ Evelyn CJA, Money-Coutts G. B., Tyrrell J. A. The Seven Circles Theorem and Other New Theorems (англ.). — London: Stacey International, 1974. — P. 49—58. — ISBN 978-0-9503304-0-2.
- ↑ Evelyn, C. J. A.; Money-Coutts, G. B.; and Tyrrell, J. A. "The Seven Circles Theorem." §3.1 in The Seven Circles Theorem and Other New Theorems. London: Stacey International, pp. 31-37, 1974.
- ↑ Seven circles theorem. Теорема о шести окружностях (англ. яз.)// https://en.wikipedia.org/wiki/Seven_circles_theorem
Литература
- Wells D. The Penguin Dictionary of Curious and Interesting Geometry (англ.). — New York: Penguin Books, 1991. — P. 231. — ISBN 0-14-011813-6.
Ссылки
- Weisstein, Eric W. Six Circles Theorem (англ.) на сайте Wolfram MathWorld.
- The Six Circle Theorem revisited by D. Ivanov and S. Tabachnikov