Гипотенуза
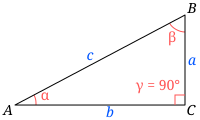
Гипотенуза (греч. ὑποτείνουσα, натянутая[1]) — самая длинная сторона прямоугольного треугольника, противоположная прямому углу.
Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: Квадрат длины гипотенузы равен сумме квадратов длин катетов. Например, если длина одного из катетов равна 3 м (квадрат его длины равен 9 м), а длина другого — 4 м (квадрат его длины равен 16 м), то сумма их квадратов равна 25 м. Длина гипотенузы в этом случае равна квадратному корню из 25, то есть 5 м.
Вычисление длины гипотенузы[править | править код]
Длину гипотенузы можно найти, применив теорему Пифагора.
Пусть и — длины катетов, тогда гипотенузу можно найти по формуле
Если известна длина одного из катетов и угол, отличный от прямого, то можно найти длину гипотенузы по формулам:
- для противолежащего угла , и
- для прилежащего угла .
См. также[править | править код]
Примечания[править | править код]
- ↑ Александрова Н. В. Математические термины.(справочник). М..: Высшая школа, 1978, с. 26.







