Двойственный граф
Двойственный граф к планарному графу — это граф, в котором вершины соответствуют граням графа ; две вершины соединены ребром если и только если соответствующие им грани графа имеют общее ребро. Например, двойственны друг к другу графы куба и октаэдра.
Термин двойственный используется ввиду того, что это свойство симметрично — если H двойственен G, то G двойственен H (при условии, что G связен). То же самое понятие можно использовать для вложения графов в многообразия. Понятие двойственности графов отличается от рёберно-вершинной двойственности (рёберный граф) графа и эти два понятия не следует путать.
Свойства[править | править код]

- Двойственный граф является псевдографом: в нём могут быть петли и кратные рёбра.
- Двойственный планарному граф является плоским мультиграфом.
- Если G является связным графом и если G′ — двойственен G, то G двойственен G′.
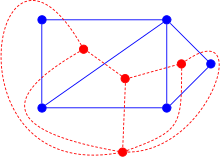
- Поскольку двойственный граф зависит от способа укладки, к одному и тому же планарному графу могут существовать несколько двойственных (неизоморфных). На рисунке красные графы не изоморфны, поскольку верхний имеет степень 6 (внешняя грань). Однако если граф 3-связен, как показал Уитни, укладка единственна, а потому и двойственный граф единственен[1].
Ввиду двойственности, для любого результата, использующего число граней и вершин, можно обменять эти величины.
Самодвойственным называют граф, который изоморфен своему двойственному графу. Например, самодвойственен граф тетраэдра.
Алгебраическая двойственность[править | править код]
Пусть G — связный граф. Алгебраически двойственным графу G называется граф G★ такой, что G и G★ имеют одно и то же множество рёбер, любой цикл в G является разрезом G★ и любой разрез G является циклом в G★. Любой планарный граф имеет алгебраически двойственный граф, в общем случае не единственный (двойственный граф определяется укладкой). Обратное тоже верно — как показал Хасслер в своём критерии планарности[2], связный граф планарен в том и только в том случае, если он имеет алгебраически двойственный граф.
Тот же факт можно выразить в терминах теории матроидов: если M является графовым матроидом[англ.] графа G, то двойственным матроидом[англ.] M является графовый матроид в том и только случае, когда G планарен. Если G планарен, двойственный матроид является графовым матроидом двойственного G графа.
Слабая двойственность[править | править код]
Слабодвойственный планарному графу — это подграф двойственного графа, в котором вершины соответствуют ограниченным граням исходного графа. Планарный граф является внешнепланарным в том и только в том случае, когда двойственный является лесом, и планарный граф является графом Халина в том и только в том случае, когда его слабодвойственный является двусвязным и внешнепланарным. Для любого планарного графа G, пусть G+ — планарный мультиграф, образованный добавлением одной вершины v в неограниченную грань графа G и соединением v со всеми вершинами внешней грани (несколько раз, если вершина появляется несколько раз на границе грани). Теперь G является слабодвойственным (планарного) двойственного G+ графа[3][4].
Примечания[править | править код]
- ↑ Adrian Bondy, U.S.R. Murty. глава «Planar Graphs», Theorem 10.28 // Graph Theory. — Springer, 2008. — Т. 244. — С. 267. — (Graduate Texts in Mathematics). — ISBN 9781846289699. — doi:10.1007/978-1-84628-970-5.
- ↑ Hassler Whitney. Non-separable and planar graphs // Transactions of the American Mathematical Society. — 1932. — Т. 34, вып. 2. — С. 339–362. — doi:10.1090/S0002-9947-1932-1501641-2.
- ↑ Herbert J. Fleischner, D. P. Geller, Frank Harary. Outerplanar graphs and weak duals // Journal of the Indian Mathematical Society. — 1974. — Т. 38. — С. 215–219.
- ↑ Maciej M. Sysło, Andrzej Proskurowski. Graph Theory: Proceedings of a Conference held in Lagów, Poland, February 10–13, 1981. — Springer-Verlag, 1983. — Т. 1018. — С. 248–256. — (Lecture Notes in Mathematics). — doi:10.1007/BFb0071635.
Ссылки[править | править код]
- Weisstein, Eric W. Dual graph (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Self-dual graph (англ.) на сайте Wolfram MathWorld.
Для улучшения этой статьи желательно:
|

