Квадратная решётка
| |
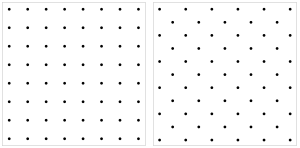
| Вертикальный квадрат Simple |
Диагональный квадрат Centered |
|---|---|

Квадратная решётка — это вид решётки в двумерном евклидовом пространстве. Решётка является двумерной версией целочисленной решётки и обозначается Z2[1]. Решётка является одной из пяти типов двумерных решёток, классифицированных по группам симметрии[2], Группа симметрии решётки в обозначениях IUC — p4m[3], в нотации Коксетера[англ.] — [4,4][4], а в орбифолдной нотации[англ.] — *442[5].
Две ориентации решётки наиболее популярны. Обычно квадраты решётки размещаются так, что стороны квадрата вертикальны и горизонтальны (будем называть это вертикальной решёткой), либо стороны квадратов расположены под углом 45 градусов по отношению к осям. В последнем случае решётку иногда называют центрированной квадратной решёткой[6].
Симметрия[править | править код]
Симметрия квадратной решётки — это группа обоев p4m. Орнамент с этой решёткой симметрии переноса не может иметь более высокую степень симметрии, чем сама решётка, но может иметь меньшую степень. Вертикальную квадратную решётку можно рассматривать как диагональную решётку с размером сетки в √2 раза больше и центры этой решётки находятся в центре квадратов. Соответственно, после добавления центров квадратов в квадраты вертикальной решётки мы получаем решётку в √2 раза меньшую исходной решётки. Орнамент с 4-кратной вращательной симметрией имеет квадратную решётку 4-кратных центров вращения, которая в √2 раза мельче и расположена диагонально по отношению к исходной решётке симметрии переноса.
По отношению осей отражения существует три возможных ситуации:
- Отсутствие симметрии. Это группа обоев p4.
- В четырёх направлениях. Это группа обоев p4m.
- В двух перпендикулярных направлениях. Это группа обоев p4g. Точки пересечения осей отражения образуют квадратную решётку, которая по размерам и по направлениям совпадает с квадратной решёткой центров вращения.
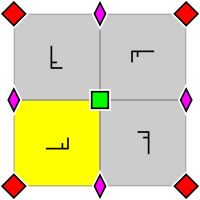
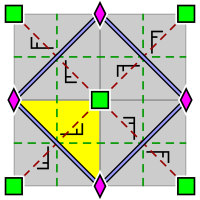
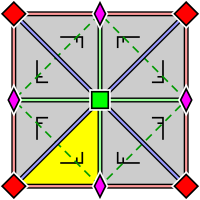
| p4, [4,4]+, (442) | p4g, [4,4+], (4*2) | p4m, [4,4], (*442) |
|---|---|---|
|
|
|
| Группа обоев p4, с расположением внутри примитивной ячейки 2- и 4-кратных центров вращения (верно и для p4g и p4m). Фундаментальная область показана жёлтым цветом. | Группа обоев p4g. Есть оси отражения в двух направлениях, не проходящие через 4-кратные центры вращения. | Группа обоев p4m. Есть оси отражения в четырёх направлениях, проходящие через 4-кратные центры вращения. В двух направлениях оси отражения ориентированы так же и с той же плотностью, что и для p4g, но сдвинуты. В двух направлениях они в √2 плотнее. |
См. также[править | править код]
- Центрированное квадратное число
- Евклидов сад[англ.]
- Гауссовы целые числа
- Шестиугольная решётка
- Квинкункс[англ.]
- Квадратный паркет
Примечания[править | править код]
- ↑ Conway, Sloane, 1999, с. 106.
- ↑ Golubitsky, Stewart, 2003, с. 129.
- ↑ Field, Golubitsky, 2009, с. 47.
- ↑ Johnson, Weiss, 1999, с. 1307–1336, см. стр 1320.
- ↑ Schattschneider, Senechal, 2004, с. 53–72.
- ↑ Johnston, Richman, 1997, с. 159.
Литература[править | править код]
- Conway John, Sloane Neil J. A. Sphere Packings, Lattices and Groups. — Springer, 1999. — С. 106. — ISBN 9780387985855.
- Golubitsky Martin, Stewart Ian. The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space. — Springer, 2003. — Т. 200. — С. 129. — (Progress in Mathematics). — ISBN 9783764321710.
- Michael Field, Golubitsky Martin. Symmetry in Chaos: A Search for Pattern in Mathematics, Art, and Nature. — 2nd. — SIAM, 2009. — С. 47. — ISBN 9780898717709.
- Johnson Norman W., Weiss Asia Ivić. Quadratic integers and Coxeter groups // Canadian Journal of Mathematics. — 1999. — Т. 51. — С. 1307–1336. — doi:10.4153/CJM-1999-060-6.. См. начало страницы 1320.
- Schattschneider Doris, Senechal Marjorie. Handbook of Discrete and Computational Geometry. — 2nd. — CRC Press, 2004. — С. 53–72. — ISBN 9781420035315.. См. таблицу на стр. 62 Архивная копия от 14 марта 2022 на Wayback Machine.
- Johnston Bernard L., Richman Fred. Numbers and Symmetry: An Introduction to Algebra. — CRC Press, 1997. — С. 159. — ISBN 9780849303012.